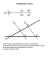Twierdzenie Poincaré –Bendixsona

Twierdzenie Poincaré–Bendixsona
1
Twierdzenie Poincaré1–Bendixsona2
1
Twierdzenie Poincaré–Bendixsona
W bieżącym podrozdziale zakładamy, że U jest otwartym podzbiorem płaszczyzny R2 i F : U → R2 jest polem wektorowym klasy C 1 , generującym
lokalny potok ϕ.
Twierdzenie 1 (Twierdzenie Poincaré–Bendixsona). Niech dla pewnego x ∈
U zbiór ω(x) będzie niepustym zbiorem zwartym nie zawierającym punktów
stacjonarnych. Wówczas ω(x) jest orbitą okresową.
W dowodzie twierdzenia Poincaré–Bendixsona wykorzystuje się następujący wynik:
Twierdzenie 2 (Twierdzenie Jordana3 o rozcinaniu płaszczyzny). Niech
J ⊂ R2 będzie krzywą zwykłą zamkniętą (tzn. zbiorem homeomorficznym z
okręgiem). Wówczas dopełnienie R2 \ J ma dwie składowe spójności, jedną
ograniczoną (wnętrze krzywej J), i drugą nieograniczoną (zewnętrze krzywej
J). Ponadto, J jest wspólnym brzegiem swojego wnętrza i zewnętrza.
Przystępujemy teraz do dowodu twierdzenia Poincaré–Bendixsona.
Jeśli O(x) jest orbitą okresową, to nie ma czego dowodzić. Załóżmy zatem, że x nie jest punktem okresowym, oraz że ω(x) jest niepustym zbiorem
zwartym nie zawierającym punktów stacjonarnych.
Przypomnijmy dwuwymiarową wersję
twierdzenia o lokalnym prostowaniu pola wektorowego:
Twierdzenie 3 (Twierdzenie o prostowaniu pola wektorowego — wersja
dwuwymiarowa). Niech F : U → R2 będzie polem wektorowym klasy C 1 i
niech u ∈ U będzie punktem regularnym pola F. Wówczas istnieją:
• transwersala L pola F w punkcie u,
• otoczenie otwarte V punktu u,
1
Henri Poincaré (1854 – 1912), matematyk francuski, według kompilatora (J. M.) jeden
z najwybitniejszych matematyków wszech czasów
2
Ivar Otto Bendixson (1861 – 1935), matematyk szwedzki
3
(Marie Ennemond) Camille Jordan (1838 – 1922), matematyk francuski (od jego nazwiska pochodzi też postać Jordana macierzy; nie należy go mylić z Wilhelmem Jordanem
(1842 – 1899), geodetą i matematykiem niemieckim, od którego nazwiska pochodzi algorytm Gaussa–Jordana)
2
Twierdzenie Poincaré–Bendixsona
• liczby dodatnie ε, δ, oraz dyfeomorfizm
1−1
M : V −−→ (−δ, δ) × (−ε, ε)
na
klasy C 1
o następujących własnościach:
(i) M(L) = (−δ, δ) × {0}; ponadto M(u) = (0, 0),
(ii) dla każdego v ∈ V istnieje dokładnie jedna para (w, t) ∈ L × (−ε, ε)
taka, że v = ϕt (w); ponadto, M(v) = (ξ, t), gdzie M(w) = (ξ, 0).
Oznaczmy M = (M1 , M2 ).
Fakt 1. Niech y ∈ ω(x). Wówczas istnieją transwersala L pola F w punkcie
y oraz ciąg (ϕtk (x)) ⊂ L, tk → ∞ gdy k → ∞, zbieżny do y.
Dowód. Niech sk → ∞ będzie ciągiem takim, że ϕsk (x) dąży do y. Oznaczmy
przez L (odp. V ) transwersalę (odp. otoczenie) punktu y jak w twierdzeniu o
lokalnym prostowaniu (Tw. 3). Odrzucając skończenie wiele wyrazów, można
założyć, że wszystkie ϕsk (x) należą do V . Określmy tk := sk − M2 (ϕsk (x)).
Po pierwsze, zauważmy że, na podstawie Tw. 3(ii),
ϕtk (x) = ϕsk −M2 (ϕsk (x)) (x) ∈ L.
Dalej, korzystając z własności (PL2) oraz z ciągłości potoku lokalnego (patrz,
np., wykład o lokalnym prostowaniu), widzimy, że
ϕsk −M2 (ϕsk (x)) (x) = ϕ−M2 (ϕsk (x)) (ϕsk (x))
dąży, przy k → ∞, do ϕ−M2 (y) (y), które jest równe, znów na podstawie (znów
na podstawie Tw. 3(ii)), y.
Wystarczy teraz zauważyć, że tk ­ sk −ε, zatem tk → ∞ gdy k → ∞.
Fakt 2. Niech y ∈ ω(x). Wówczas dla każdej transwersali L pola F w punkcie
y jak w Fakcie 1, każdy ciąg (ϕtk (x))∞
k=1 ⊂ L zbieżny do y i taki, że 0 < t1 <
t2 < · · · < tk < tk+1 < · · · , jest monotoniczny.
Monotoniczność rozumiemy w następujący sposób: ciąg (M1 (ϕtk (x)))∞
k=1
jest monotoniczny.
Twierdzenie Poincaré–Bendixsona
3
Dowód Faktu 2. Załóżmy najpierw nie wprost, że M1 (ϕtk (x)) i M1 (ϕtk+1 (x))
są, dla pewnego k ∈ N, przeciwnych znaków.
Wówczas zbiór J, będący sumą odcinka transwersali L o końcach ϕtk (x)
i ϕtk+1 (x), i „kawałka” orbity { ϕt (x) : t ∈ [tk , tk+1 ] }, jest krzywą zwykłą
zamkniętą (patrz poniższy rysunek, gdzie x1 := ϕtk (x), x2 := ϕtk+1 (x)).
x1
y
x2
y−1
Zauważmy, że na odcinku transwersali L łączącym punkty x1 i x2 pole
wektorowe F skierowane jest na zewnątrz krzywej J. Wynika stąd, że dla
s < 0 dostatecznie bliskich zeru punkt ϕs (y) jest położony wewnątrz krzywej
J. Ustalmy takie s, i oznaczmy y−1 := ϕs (y). Lecz y−1 ∈ ω(x), zatem istnieje
ϑ > tk+1 takie, że ϕϑ (x) leży wewnątrz krzywej J. Lecz jest to niemożliwe,
bo dodatnia półorbita punktu x2 nie ma jak wejść do wnętrza krzywej J: nie
może przeciąć zbioru { ϕt (x) : t ∈ [tk , tk+1 ] } (przeczyłoby to założeniu, że x
nie jest punktem okresowym), i nie może wejść do wnętrza krzywej J przez
odcinek transwersali (gdyż tam pole wektorowe skierowane jest na zewnątrz).
Załóżmy teraz nie wprost, że, na przykład, 0 < M1 (ϕtk (x)) < M1 (ϕtk+1 (x))
dla pewnego k ∈ N.
Wówczas zbiór J, będący sumą odcinka transwersali L o końcach ϕtk (x)
i ϕtk+1 (x), i „kawałka” orbity { ϕt (x) : t ∈ [tk , tk+1 ] }, jest krzywą zwykłą
zamkniętą (patrz poniższy rysunek, gdzie x1 := ϕtk (x), x2 := ϕtk+1 (x)).
4
Twierdzenie Poincaré–Bendixsona
y
x1
x2
Teraz punkt y leży wewnątrz krzywej J. Lecz jest to niemożliwe, bo
(tak jak w poprzedniej części dowodu) dodatnia półorbita punktu x2 nie ma
którędy wejść do wnętrza krzywej J.
Lemat 1. Niech y ∈ ω(x). Wówczas dla każdej transwersali L pola F w
punkcie y jak w Fakcie 1 zachodzi ω(x) ∩ L = {y}.
Dowód. Załóżmy nie wprost, że ξ 6= y ∈ ω(x) ∩ L. Zachodzi M1 (ξ) 6= 0 =
M1 (y). Załóżmy, że 0 ¬ s′ < s′′ są takie, że ϕs′ (x) ∈ L i ϕs′′ (x) ∈ L.
Z twierdzenia o lokalnym prostowaniu pola wektorowego (Tw. 3) wynika,
że s′′ − s′ > 2ε. Zatem zbiór tych chwil t ­ 0, dla których ϕt (x) należy
do transwersali L, jest co najwyżej przeliczalny. Zbiór ten (oznaczany przez
(tk )) jest w istocie przeliczalny, gdyż y ∈ ω(x). Dla pewnego podciągu (tkl )
zachodzi ϕtkl (x) → y, czyli M1 (ϕtkl (x)) → 0, zaś dla innego podciągu (tkl′ )
zachodzi ϕtk′ (x) → ξ, czyli M1 (ϕtk′ (x)) → M1 (ξ) 6= 0. Lecz, na podstawie
l
l
Faktu 2, ciąg (M1 (ϕtk (x)) jest monotoniczny, sprzeczność.
Lemat 2. Niech y ∈ ω(x). Wówczas y jest punktem okresowym.
Dowód. Z tego, że ω(x) jest zwarty i niezmienniczy wynika, że ∅ =
6 ω(y) ⊂
ω(x). Ustalmy z ∈ ω(y). Fakt 1 zastosowany do z ∈ ω(y) gwarantuje nam
istnienie transwersali L pola F w punkcie z i ciągu (tk ) rozbieżnego do ∞
Twierdzenie Poincaré–Bendixsona
5
takiego, że ϕtk (y) ∈ L oraz ϕtk (y) dąży do z gdy k → ∞. O ciągu (tk )
możemy założyć, że jest rosnący. Lecz z Lematu 1 (zastosowanego do z ∈
ω(x)) wynika, że ϕt1 (y) = ϕt2 (y) = z, gdzie t1 < t2 , zatem y jest punktem
okresowym.
Wykazaliśmy zatem, że ω(x) jest sumą orbit okresowych.
Aby dokończyć dowód twierdzenia Poincaré–Bendixsona, ustalmy y ∈
ω(x), i oznaczmy przez T > 0 okres podstawowy orbity okresowej Γ = O(y)
(oczywiście Γ ⊂ ω(x)). Rozważmy znów transwersalę L w punkcie y i otoczenie V . Z ciągłej zależności rozwiązania od warunków początkowych wynika,
że dla każdego η > 0 istnieje otoczenie otwarte V ′ ⊂ V punktu y takie, że
(i) kϕt (z) − ϕt (y)k < η dla dowolnego z ∈ V ′ i wszystkich t ∈ [0, T + ε],
(ii) ϕT (V ′ ) ⊂ V .
Załóżmy dalej, że otoczenie otwarte V ′ jest wypukłe.
Ustalmy η > 0, i dobierzmy V ′ do η. Istnieje s > 0 takie, że ϕs (x) ∈
L ∩ V ′ . Z (ii) wynika, że punkt ϕs+T (x) ∈ V . Z twierdzenia o prostowaniu
pola wektorowego (Twierdzenie 3) wynika istnienie ϑ ∈ (−ε, ε) takiego, że
ϕs+T +ϑ (x) ∈ L. Z (i) wynika, że kϕt+s (x) − ϕt (y)k < η dla wszystkich t ∈
[0, T + ε].
Z monotoniczności (Fakt 2) wynika, że punkt ϕs+T +ϑ (x) musi leżeć na
transwersali L pomiędzy punktami ϕs (x) i y. Ponieważ otoczenie V ′ jest
wypukłe, punkt ϕs+T +ϑ (x) należy do V ′ . Powtarzamy teraz powyższe rozumowanie, otrzymując, że dla wszystkich t ­ s punkt ϕt (x) jest w odległości
mniejszej niż η od orbity okresowej Γ. Wynika stąd, że ω(x) ⊂ Γ, co kończy
dowód twierdzenia Poincaré–Bendixsona.
Orbitę okresową O(y) taką, że istnieje x ∈
/ O(y), dla którego ω(x) =
O(y), nazywamy cyklem granicznym.
2
Dalsze własności pól wektorowych na płaszczyźnie
Sformułujemy teraz dwa twierdzenia z topologii, które będą potrzebne w
późniejszych rozważaniach.
Twierdzenie 4 (Twierdzenie Schönfliesa4 ). Niech J ⊂ R2 będzie krzywą
zwykłą zamkniętą i niech h : J → T, gdzie T = { x ∈ R2 : kxk = 1 }, będzie homeomorfizmem. Wówczas istnieje homeomorfizm H : R2 → R2 będący
rozszerzeniem homeomorfizmu h (tzn. H|J = h i H −1|T = h−1 ).
4
Arthur Moritz Schönflies (1853 – 1928), matematyk niemiecki
Twierdzenie Poincaré–Bendixsona
6
Przed sformułowaniem następnego twierdzenia, przypomnijmy, że punktem stałym odwzorowania f : X → X (X jest dowolnym zbiorem) nazywamy
x ∈ X taki, że f (x) = x. Jeśli X jest przestrzenią metryzowalną (ogólniej:
przestrzenią topologiczną Hausdorffa) i f jest odwzorowaniem ciągłym, to
zbiór punktów stałych odwzorowania f (być może pusty!) jest domknięty.
Przestrzeń metryzowalną homeomorficzną z domkniętą kulą jednostkową
w n-wymiarowej przestrzeni euklidesowej nazywamy dyskiem n-wymiarowym.
Twierdzenie 5 (Twierdzenie Brouwera5 o punkcie stałym). Ciągłe odwzorowanie dysku n-wymiarowego w siebie ma punkt stały.
Twierdzenie 6. Niech F : U → R2 będzie polem wektorowym klasy C 1 , i
niech Γ będzie orbitą okresową pola F taką, że jej wnętrze zawarte jest w U.
Wówczas wewnątrz Γ istnieje y taki, że F(y) = 0.
Dowód. Jako że Γ jest podzbiorem płaszczyzny R2 homeomorficznym z okręgiem, na podstawie twierdzenia Schönfliesa istnieje homeomorfizm płaszczyzny R2 na R2 przeprowadzający sumę D krzywej Γ i jej wnętrza D0 na (domknięte) koło jednostkowe. Wobec tego, D jest dyskiem dwuwymiarowym.
Oznaczmy przez Φ potok lokalny generowany przez pole wektorowe F.
Dla każdego x ∈ D0 orbita O(x) jest, jako zbiór spójny, zawarta w D0 .
Wynika stąd, że D0 jest zbiorem niezmienniczym, i, co za tym idzie, dysk
dwuwymiarowy D też jest zbiorem niezmienniczym. Ponieważ D jest zbiorem
zwartym, ϕt (x) jest określone dla każdego t ∈ R i każdego x ∈ D.
Dla k ∈ N oznaczmy przez Ek zbiór punktów stałych odwzorowania
Ψk : D → D, Ψk (x) := ϕ1/2k (x). Z twierdzenia Brouwera o punkcie stałym
wynika, że zbiory Ek , k ∈ N są niepuste Ponadto, zbiory te są domknięte,
T
zatem zwarte. Dalej, Ek+1 ⊂ Ek . Wynika stąd, że E := ∞
k=1 Ek jest, jako przekrój zstępującej rodziny niepustych zbiorów zwartych, też niepusty i
zwarty.
Weźmy y ∈ E. Z definicji zbioru E wynika, że ϕt (y) = y dla t > 0
dwójkowo wymiernych. Lecz odwzorowanie R ∋ t 7→ ϕt (x) jest ciągłe, zatem
ϕt (x) = y dla każdego t > 0, czyli F(y) = 0.
Fakt, że E ∩ Γ = ∅, jest oczywisty.
Wniosek. Niech F : R2 → R2 będzie polem wektorowym klasy C 1 takim, że
O + (x) ma zwarte domknięcie, dla pewnego x. Wówczas istnieje y takie, że
F(y) = 0.
Dowód. Zbiór ω(x) jest zwarty i niepusty. Jeśli ω(x) zawiera punkt stacjonarny y, to teza wniosku jest spełniona. Jeśli nie, to na podstawie twierdzenia
5
Luitzen Egbertus Jan Brouwer (1881 – 1966), matematyk holenderski
Twierdzenie Poincaré–Bendixsona
7
Poincaré–Bendixsona (Tw. 1) ω(x) jest orbitą okresową Γ. Lecz z Tw. 6
wynika istnienie (wewnątrz krzywej Γ) punktu y takiego, że F(y) = 0.