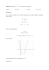c - Strona 1

WŁASNOŚCI FUNKCJI KWADRATOWEJ - zakres podstawowy
GRUPA
A
Uwaga! Rozwiązania zapisujemy na osobnej, estetycznej i podpisanej kartce formatu A5.
W zadaniach zamkniętych wybraną literę przekreślamy X a błędne oznaczenie otaczamy okręgiem X .
1. (1p) Na rysunku obok przedstawiony jest wykres funkcji o wzorze:
=
A.
–2
= −
C.
+ 2
+ 1
=
B.
–1
= −
D.
<0i
Uzasadnienie: Z wykresu odczytujemy:
+ 2
− 2
− 1
–1
= 2, −1 i dopasowujemy wzór.
2. (1p) Parabola, która jest wykresem funkcji
= 2
ma wierzchołek o współrzędnych:
A. 1, −4
B. −1,4
C. 4, −1
= −1 i
Uzasadnienie: Z postaci kanonicznej
=
=
C.
=
+
−
−
−
B.
=
D.
=
Uzasadnienie: Ponieważ współczynnik
=
Np.
+
−
=
−
+
przy
= −1,4 .
+
−
to:
−
+
jest równy
+2∙ ∙ ∙
+ 4,
D. −4,1
= 4 zatem
3. (1p) Wzór w postaci kanonicznej funkcji
A.
+ 1
+ ∙ −
to rozwijamy tylko funkcje z punktów A i B i porównujemy.
=
+
− .
4. (1p) Funkcja kwadratowa, której wykres przechodzi przez punkty 0, −2 , 1, −5 , −2, −14 , ma wzór:
A.
=
−4 −2
= −
B.
− 2 − 2 C.
= 3
−2
D.
= −3
−2
Uzasadnienie: Wykresy wszystkich funkcji przechodzą przez punkt 0, −2 bo ! = −2 . Sprawdźmy punkt −2, −14 .
Do wzorów określających funkcje wstawiamy w miejsce pierwszą współrzędną punktu i obliczamy wartość .
A. = 10,
B. = −2,
C. = 10,
D. = −14. Wygląda, że to funkcja z punktu D, ale sprawdźmy czy
jej wykres przechodzi przez punkt 1, −5 . Postępujemy analogicznie i otrzymujemy D. = −5. To potwierdza
nasze przypuszczenie.
5. (1p) Funkcja określona wzorem
A.
" = 0
B. " = −
= − −
C. " =
+ " ma jedno miejsce zerowe dla:
D. " = −1
Uzasadnienie: Funkcja kwadratowa ma jedno miejsce zerowe gdy ∆= 0. Zatem 1 + 4" = 0 . Otrzymujemy " = − .
6. (1p) Funkcja kwadratowa o miejscach zerowych −2 i 5, której wykres przechodzi przez punkt
1,24 , ma wzór:
A. =
− 2
+ 5
B. = 24 − 2
+ 5
C.
= −2
+ 2
− 5
D.
= 2
− 2
+ 5
Uzasadnienie: Z podanych wzorów widać, że tylko funkcja z punktu C. ma miejsca zerowe −2 i 5. Sprawdźmy czy jej wykres
przechodzi przez punkt 1,24 : = −2 1 + 2 1 − 5 = −2 ∙ 3 ∙ −4 = 24.
7. (2p) Oblicz współrzędne punktów przecięcia wykresów funkcji
=
−4 −3 i
= − + 1.
Rozwiązanie: Punkt wspólny wykresów funkcji to punkt , , którego współrzędne spełniają układ równań:
=
− 4 − 3+
*
, a jego rozwiązaniem są dwie pary liczb: −,, - i ., −/ , są to zarazem szukane punkty.
= − + 1
Odpowiedź: Punktami przecięcia wykresów danych funkcji są: −,, - i ., −/ .
8. (4p) Dana jest funkcja kwadratowa
=
− − .
a) Oblicz współrzędne wierzchołka paraboli, która jest wykresem tej funkcji.
b) Oblicz miejsca zerowe tej funkcji.
c) Narysuj wykres tej funkcji.
d) Zbadaj monotoniczność tej funkcji.
Rozwiązanie:
a) Ze wzorów na
=−
∆= 1 + 3 = 4,
4
0
1
i
= ,
=−
∆
1
obliczamy współrzędne wierzchołka:
= −1 zatem 2 =
6
,
-
, −, ,
b) √∆= 2,
=
=− ∨ =
= ,
c)
d) Znamy współrzędne wierzchołka paraboli oraz współczynnik a
możemy określić monotoniczność funkcji.
Funkcja jest malejąca dla ∈ −∞, + 9 oraz
funkcja jest rosnąca dla
∈ : + , +−∞ .
Odpowiedź: a) Wierzchołkiem jest punkt 2 =
,
,
, −, ,
/
b) Pierwiastkami równania są ; = − ∨ ; =
c) Wykres obok
d) Funkcja jest malejąca dla ∈ −∞, + 9 oraz funkcja jest rosnąca dla
∈ : + , +−∞ .
9. (3p) Rozwiąż nierówności:
a) −2
> 32
b) − =
+ = ≤0
c) −2 + 10 − 8 > 0
Rozwiązanie:
a) −2
> 32 lewa strona nierówności jest niedodatnia a prawa ujemna, zatem ; ∈ ∅,
b) − =
+
=
≤ 0, przekształcamy − =
odczytujemy

Odpowiedź: a) ; ∈ ∅,
− 3 ≤ 0 i z wykresu
∈ −∞,+ +09 ∪ :3+, ++∞
c) −2 + 10 − 8 > 0 znajdujemy miejsca zerowe
i z wykresu odczytujemy ∈ 1+, +4
b) ; ∈ −∞+, +B9 ∪ :/+, ++∞
= 1∨
=4
c) ; ∈ ,+, +.
10. (5p) Drut o długości 100 !C chcemy wygiąć w prostokątną ramkę.
Oblicz, jakie wymiary powinna mieć ta ramka, aby prostokąt, który ogranicza, miał największe pole.
Rozwiązanie:
a) 2 + 2 = 100 oraz D
= ∙ . Wyznaczamy y i wstawiamy do wzoru funkcji na pole:
D
dla
=
=
∙ 50 −
czyli D
= − + 50 . Funkcja ta przyjmuje wartość największą
=E
gdzie = −
= 25 i wtedy = 25 F = 25.
∙ 4
Odpowiedź: Prostokąt ten jest kwadratem o boku ; = -G HI.