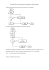wych procesu kompresji. Kompresja fraktalna dotyczy zasadniczo
Transkrypt
wych procesu kompresji. Kompresja fraktalna dotyczy zasadniczo
! " # $ $ % &' ( & ! " % ) $ * ) $ ) # + ! " + , # ) & - . &. + & $ % + / # ) # ! 0 & ) + ! . # + ! " ( ' ) $ # , + ' 0 $ &. $ 0 / ) % 0
% , ! ) . ) ! + ' # + ! " &. ! . / # + ! " % # &$ 1 ) wych procesu kompresji.
Kompresja
fraktalna dotyczy zasadniczo obrazów i jest w pewnym stopniu przeniesieniem
$ ' $ ) # + . ) !' # ) / # ' + # ! . / 2 ) . . . . + 2 , ) # $ ' # + ! "
% $ % &' * % ' & -
fragmentów innymi fragmentami tego samego obrazu. W algory
)# $ )% 2 # + % (
$ + ) # + ! " 32 $ 4 ( $ & 0 & $ ! &+ # ) $ &+ % / # ) # + % . 2 ) . + / # ) # / ( 1 / $ # ' % / 2 ) # / % ! ) 1 / 2 ) . 5 6 ) ) % + + ! " . + 2 , 7
& . 0 . ) # + ) $ ! ! & $ % &' & ) # 0 + ' ! + 5 2 - 0 ! + % &$ 1 ) + % . 0 % !)1/ 2 ). (
0 . # ) !' - $ ) # / zbioru
danych o charakterze obrazowym. W rozdziale tym przedstawiono jedynie wybrane
% # + 2 + & $ * ) $ ) # + ! " ( $ ) % / 0 % ! . . % 8 / # 0 $ # ! !' , 0 ! 0 & ) . )1 ) # ) $ * ) $ ) # + ! " 5 6 & ) ) ! " ) ) $ + & + $ ) ) / + % $ % &' * ) $ ) # ' . & ) 1 ) & . ! . / 1 # ) & ! " % ) % 2 $ + % ) . ) ! ' ) $ + ! . # '
. + $ 1 ) / $ ) . 1# # ) + 2 ) # + % ) & $ ) % . ) / )
dnienia optymalizacji
takiego schematu.
12.1. Wprowadzenie
9 2 $ + + & - ' 0 ! . + . % )' 0 # ! ! " + & ) % 2 7 & ) ( & 0 , # ) ) # 2 ) . + . ) )' 0 8 ! . # * ) / % # + & ) % 2 # . )' % # 2 # 5 : . # - ) ) * ) $ ) # ) ; <= & ) ! .+ 1 ) ! + . + ' # # ) . - . ) % ) # )
ostatnich
latach geome
) $ ! " 2 $ ( ! & ) 1 & - & ) 0 $ % &' * ) $ ) # ' 3 ) # / 5 * ) ! ) ! % & & #
FC) [2],& konsekwentnie
udoskonalanej w pracach Barnsleya, Jacquina i Beaumonta [3][4][5].
- # ) . ' ! ) + ! + ' # + ! " . + ) $ * ) $ ) 2 $ & ) % 2 # + ! "
Opiera
& . $ ) # ) , # + ! " * ) / % # 2 ) . ( $ & 0 . + 2 , # . )' % # 2 # 5
9 $ ) # . )' % # / 2 7 & ) + 2 ) # + ! " * ) / % # 2 ) . . # 0 &$ 7 ! . # 0
$ 1 ) # ! 0 ( ) # ) & - # . ) & - ) # * ) / % # + / # ) # + ! "
. + 2 , # + % ' & * % 0
$ ) # + . ) ! ' & ) # & ) # ! ' % + $ % &' 5
6 2 7 & ' & + $ + ) # # + $ ) !' * ) / % #
* ) / % # ( ) , relacji
fragment
inny
fragment.
Wymaga
to
uogólnienia
koncepcji
iteracyjnego systemu
* # $ !' 3 > ? 4 ( $ + % ' 2 $ + & ) % 2 # ( ) - ! . / - # ) ) !' - 2 7 & )
* ) / % # ) $ ( 2 + 2' 0 8 ) $ , 2 7 & * ) / % #
typu fragment - inny fragment i
' # ! . # # ) ! 8 2 + ! " ! ! " ) / + % ! . # + ! " 5 @ ) $ % / # # % ' & $ ) # +
) ! + ' # + &+ & % * # $ !' 3A > ? 4 ( ! . + , . & ) # ) . . $ ) 2 $ ) $ # ! !' ) ) ! . 1 $ [6].
% &' ) * ) $ ) # ) ) # / 2 ) . / ) # ) $ # & $ ! ' ) ) . - , ) ' 0 ! / B
F (tj.
) ) * ) $ ) # / 4 . ) 1 )' 0 ! / . & . # 2 ) . 3 . & . 7 C ) # ) ! " ) 4 ( $ / oper
) !' ) # / ! . 0 $ / 2 ) . . 2 / ) &. + 2 $ 2 ) . + / # ) # / 5 9 ) * ) $ ) # + ' & & % 0 &. + & $ ! " + . # ) ! . # + ! " ) $ ) # + ! " ( . ) 1 )' 0 ! + ! " # )
przestrzeni kompresowanego
obrazu. Dla uzyskania wiernej rekonstrukcji obrazu
# ) , + . ) # 8 2 0 ) $ &+ % ) !' - 2 ) . . .
F(I), wówczas atraktor I*
oryginalnego' I& 2 + % . + 2 , # % 2 ) . operatora F
I.
2+
+ .# )!.+ 8
) * ) $ ) # +
)
)# / 2 ).
# ) , +
# )' D
. $ % # ) 8 ! ) 1 + # 2 ) . # ) * ) / % # + . ) # 1 ) $ ) % 3' & ) . ) 1 2 ) . 4 242
. 1 0 ! . # + ! " . . # ) ! " 5 6 1 ) $ # )' ! . - ! ' 2 $ ( . + ! . + % 2 - . % + ' # ) . + ) 8 2 $ ) % . ! . . # + 5 @ . + & - ) $ , # # + . 2 1
atków (etap pokrycia obrazu), które zwane
& 0 2 $ ) % . . # + 5 6 $ + )' 0 # 2 ) . % , / - & + & & 2 . + . ) ! " ) # 1 ) ! ) # ! ! . ) & ' 5 C $ # & 0 . 1 0 ! . # 5 E ) & - # &. $ ) & - 2 7 & ) % - . +
1 ) $ ) % $ + )' 0 ! + % ( ) $ ) # + % ' ) $ 1 ) $ F 1 ( ) 1 ) $ ) % ! + % . . 2 1 ) $ . # + ! " ! & . )1 2 ) . 5 6 2 7 & . ) , ) # ' &
. / - % # ' & ) # ' $ ) &+ ) # & * % ) !' 5 G ! + 1 ) $ ' & ) $ &+ % ) # + . .
) &+ ( $ # ) # ' # ) + 2 ) # + % 1 ) $ F 1 + % ( . +
wynik
pewnej
transformacji
z
tej
kl
! . + % + # $ ' ) # & * % ) !' # # 2 + 8 1 ) $ % . . # # + ! . # ' . . . # 0
1 ) $ ) ! / 5 6 . $ &. ) 1 ! # # )' ! . - ! ' ' & & ) ) # ( ' 5 &$ 1 ) ) & - . # . ) , # + ! " . $ &. ) 1 ! 7 H / % + ! . # / 3 . . # + 4 ) . ) ! 3 &$ ) & . ) ! 4 ( . +
! . + % . $ &. )1! # / % + ! . # ' & . $ &. )1! # % ) * # ! . # + % ( ) . $ &. )1! # )
) ! &. $ ' & - . ) , # & ) ! % ) # ' 5
C 1 0 ) $ &+ % ) !' 3 ) & ) # ) ( $ ) # + . ) !' 4 1 ) $ ) ! / . . 1 ) $
2 - 0 ! + ) # & * % ) !' 0 1 ) $ ) F 1 / $ ) # + ' & . + , + ! , # + ! " # % 3 ) $ ! " ' ) $
& % % ( 2 1 0 # $ ) ) + ( % ) # ) ( 54 ( . + ! . + % % # % ) # ) ) 8 / 2 1 - ) ! . + + % ) # ' ) # & * % ) !' 1 ) $ '
i najlepszym dopasowaniu danych dwóch
1) $ 5 I - ! # )' . % + ) $ 1) $ F 1 + ( $ + . ! )1 / . 2 1) $ $ + ! )
)' # )' % # ' & . + 2 1 0 ) & ) # ) . . ) + ) # + % 1 ) $ % ! + % ( & )' & - # ' / . + 2 , # %
$ # & ) # + %
2 ).
ie, a skutecznie zakodowane parametry
. $ &. )1! # ) & ) # 0 &$ % & ) # 0 & ) 8 + / # ) # / 2 ) . 5
9 + % ) . ) ! ' ) ! & $ % &' + ! . + 8 . ) # # / & & 2 + 2 1 ) ! ' # % + % + +
* $ + # ' ! " # $ $ ) # ) ) ) % . + % !+ . $ &. )1! 7 * ) $ ) # + ! " % , ) . ) !' . ) 1 $ + ! ) 2 ) . ( ' ) $ # ,
. # ) ! . # ) + % ) # + ! " . $ &. )1! 7 ( ) ) $ , . $ &. ) 1 ! 7 $ ) # + ! " 5
& # ) $ % &' % , # ) . + & $ ) 8 . . . % # ' & . # ! . 2 +
) . ( ! . + . - $ &. # . % ) 1 ) $ ( ) $ 0 $ ) # + . ) !' elementów
w
podziale
ob
# $ + ! " ) ) % . $ & . ) 1 ! # ) ( ! . + , . 1 ) / . # $ + % 2 7 & ) 1 ) $ 5
K 0 , & - . + $ . $ !' 0 $ &. ) % - ! 2 ! . # + ! " ) . . . - $ &. # %
2 1 - $ # & $ !' 5 L , # ) ) $ , # % # + ) / + % . # ) ) )
* ) $ ) # / ! . + # 8 # . ) , # + % $ % & ) # / 2 ) . 3 & & 2 $ + ! ) ( ) ) % +
. $ & . ) 1 ! # ) ) ! 1 ) $ ( $ ' # 8 $ ) # ) 1 ) $ ! + ! " 4 ( ) # # 2 ) 8
+ 2 ) . . ) , # ! . 2 ) $ ) !' 5
J
- $ &. # dla danego t
'#0
9 + % ) . ' & - ) $ , ) / + % + $ % &' $ 0 % & . + 2 $ ! + $ # ) # ) ( / + ,
. & ) + !" )
! " # $ * ) $ ) # + ! " ' & , ) ! . ) & ! " 1 # # 8 2 ! . 7
koniecznych
przy kompresji obrazu, podczas gdy czas dekompresji w najlepszych
. 0 . ) # ) ! " ' & . & - ! $ # $ &. + ;M = 5 N & ) # # / ) # 5 # ) / ) # ! . # 2 & . ) & . $ ) 7 1 ) $ ) 2 # / ' + # & 0 & . ) # + % % # $ 1
1) $ ) ! / 5 L , ' # ) $ ) . 8 # $ ych przypadkach do znacznych
. # $ &. )1! 7 2 ) . $ # & ) # + % 3# . ) &. *) / % # + 2 # + & - ' 0 2 &$ siebie w obrazie).
Technika FC, jakkolwiek stworzona na podbudowie innej teorii, w zasadach
) $ + ! . # ' ) . ) !' ' & . 2 , # ) O P 5 K 2 + ! " % ) ! " &. $ ) & - . + 2 , 7
& . ! . / # + ! " * ) / % # 2 ) . 1 / # / $ + % 2 7 & ) 3 ! " 8 , # +
& & 2 4 ( ) +' ! + % $ % &0 &$ ) F # $ + ! " . + 2 , 7 5 Q * $ + &0 . 2 , # ( . +
! . + % ) / + % + $ % &' O P . + ' & ) % ' . 1 , # ! & 0 . ) . + ! . ) ' & . + 2 & . ( ) . . / - # ) ! . - & , + ) # 0 & ) 1 0 3 ) ) # ' $ ) &+ 2 ) . 4 $ &- / - $ O P ( ) / + % +
243
? R % / 0 $ ) . ) 8 & - & $ ! . # ' & . . + ) $ ) $ ) ! ' + % ) / ) ' 0 ! + ! " $ % &' 2 ) . , ' , # # ! 5
12.2. Matematyczne podstawy kompresji fraktalnej
? ) $ ) ) % & % # ' * % ) # + % # ) . + ) # & 0 & ) % 2 # & $ + ( $ # . .
# ) / + % $ # ! + ' # + ( $ + ! " + % ) # ' & ! . 2 0 ! ) 1 $ 0 5 C ) . ' * % ) # . & . # * ) $ ) ( $ ) ' & # ) . + ) # ) ) $ , fraktal
jest elementem pewnej przestrzeni, tzw.
. & . # 0 S ) & * * ) 5 K . ! . + & ) % ' ' & # ) . + $ 1 ) % . & . # C ) # ) ! " ) 5
Niech (X,d
4 2 - . # 0 . & . # 0 % + ! . # 0 . 1 # 0 3 ' 5 ) $ 0 ( $ ' ! 0 / R ) ! " + T / % )' 0 / ) # ! 4 5 I & # 0 . + $ 1 ) . & . 7 U 2 V W X Y Z [ \ ] X ^ \ _ ` a X b c d ] e
Z V X b Y Z V X h i \ Y j Z Xk X _ X W X l Y m W ` b ] V d m Z Y X ` l ` X ^ b Y X
c a V n `c Z [
Oznaczmy przez
H(X
f g
g
g
^ W m a d j p q X _ X W X l Y j d Y Xk Z V X b Y Z V X l ` Z j d l ` X r l m _ X r [ a c Z V X b Y Z V X l `
przestrzeni X. o
g
g
H(X).
X l ` Y V d e W X Y Z[ \ s t m ^ b a c Z u u m d b c b j n l m bY s ^ k ] p [ v
Zdefiniujemy w tej przestrz
g
g
e w [ Zm r X l `X
Definicja 12.1
{
z
y
z y
y
( x , ) = max{ ( x , ), ( , x )}
(12.1)
jest nazywane | } ~
d \ Y j Z Xk d Z c d m a V c l c W X Y Z [ \ s
p V [ _` Z V X bY Z V X h
Z V X bY Z V X l `] u Z m \ Y m _` k X bY
H(X),
h
H(X),h).
g
g
X b Y Z V X h W X Y Z [ p V l m V ^ X l m i a c \ Y j Z Xk l m _ X r ] u Z m \ Y m _ X ` l m \ Y j Z Xk W c ] a V ` m m
Jest
to
prz
g
Z j r l X c Y[ ^ c X Z m Y c Z[ ` c a d V c Z c d m l ` m X l X Z^ k ] p X bY Z^ \ Y^ Z[ uZ m \ Y m _l X e
g
g
n [ _ X ` Xk V Z c V ^ W ` X h ` a X s Y [ p q c a d V c Z c d m h d Z c d m a V c l X V c bY m l ] c k s p ` m ^ l \ Y^
g
g
g
g
bY m X c Z V X \ bV Y m p X l ` m ` c a d V c Z c d m l ` m V d s r mk ] p X c i n [ d Z X b V p ` X b u c Z W ^ c d m Yd ` X Z a V X l ` X c
g
c a d V c Z c d m l `m p q V d s r mk ] p [ p q e
n s a V `X
ZV X \ bV Ymp X l `X W l m
Z V X bY Z V X l `
X. Punkt ∈
Definicja 12.2. Niech : →
g
g
Y m \ `i r X
( )=
nazywamy
~ } | ~ | } ~ } w.
ZV X \ bV Ym p X l `X
: → na przestrzeni metrycznej (X,d) zwane jest
¡ ¢£ ¤ ¥ ¦ § ¨ © ª ¤ « ¬ ® ¯ ° ° ±² ³ ° ¬ ±² ´ µ ´
0 ≤ ¶ <1 ²´· ´ « ¸
¼ ¾ » ¾ º
¼
( ( ), ( )) ≤ ½ ⋅ ( » , º ), ∀» , º ∈ ¹
(12.2)
Definicja 12.3.
¿ ° À Á Â ³ Ã ® Ä ² ´ ³ ´ Å Æ Â ´ ³ ´ ¬ ± ² Â ´ À Ç ³ · ° È É ° Ê ± Ë Ì °² Å ´ « ´ ±² ´ µ ´
s - ±² ´ µ Í É ° Ê ± Ë Ì °² Å ´ ¯Ç Î ° ³ ´ Ë Å ¬
 ±Ê Á µ Ë Å Æ ³ ³ °· ° È Å Â Ï ¸ ´ ³ °´ Ð ´ ³ Ñ Ã Ã Ð Â Å Ã À à  ´ ³ °´ Ò
Ó ¢£ £ ¡ ¢£ Ô Õ ÖÔ Ö × ¡ ¢ © Ø ¥ ¦ § ¨ © ª © Ø
Niech ¾ : ¹ → ¹ Î Ï Ð Å ° Ã Ð Â Å Ã À Ã Â ´ ³ ° È Å Â Ï ¸ ´ ¬ Í Ë Æ È ³ ´ Ê À Å ± ² À Å ³ ° È ² À Æ Ë Å ³ ¬ Å Ç Ê µ ³ ¬
(X,d). Wtedy w Ê Ã ± ° ´ Ð ´ Ð Ã · µ ´ Ð ³ ° ¬ Ð ³ Ê Ç ³ · ² ± ² ´ µ Æ » Ù ∈ ¹ Ú Û Ü Ý Þ Û ß à Ý ß á Û â Û ã ß ä å Ý Ü æ Þ â à æ
ó
ç
è
∈ é ê ë å {è ì } à Û â ê Ú ã ä è 1 = è , è ô +1 = õ ( è ô ), = í ð ñ ð ò ò ò ð ï î í Ú ö ÷ ê ä å Û ß Ý Ü æ Þ â à æ ø à Û ù ä å Ý Ú é ö ú á ê
û
ü
üÙ
lim
, ∀ü ∈
ì { ì}=
(12.3)
→∞
ýþ ÿ
ÿ
ÿ ÿ ÿ þ þ ÿ
þ ÿ
þ
obiekt przestrzeni X
ÿ
þ
ÿ
ÿ
þ
þ
244
þ
þ
þ
ÿ
þ
þ
ÿ
ÿ
ÿ
ý
þ
! þ
ÿþ
þ þ þ ÿ ÿ þ ÿ ÿ
ÿ þ
ÿ
þ
þ
ÿ
ÿ
ÿ
ÿ ÿ
ÿ
ÿ
ÿ
# þ
ÿ þ
" ÿ
Generacja fraktali przy pomocy iteracyjnego systemu funkcji
$ þ
þ
þ ÿ
þ & ÿ ÿ ÿ %
%
ÿ
Definicja 12.4. '
þ X,d
þ
1
jako { ;
0
1
ÿ
,
0
ÿ
,...,
2
3 ÿ
þ ÿ
þ
þ
}
þ
%
Twierdzenie 12 4 5 4
6
ÿ
þ
ÿ
þ
þ
H
I J K L MN
þ
ÿ þ
%
ÿ
ÿ
O P Q R K N S
d
þ
þ
þ
%
þ
ÿ
2
þ
ÿ
ÿ
þ
þ
→
ÿ
ÿ *
:
þ
ÿ
+ ,
($ )
ÿ
/
dla = 1,2,..., .
= max{2 1 , 2 2 ,..., 2 , } .
- ,
ÿ
þ
:
($ )
ÿ
9 @ 8 A? B
e
þ
þ ÿ
þ
%
- IFS).
ÿ 7 8 9 : 7 ; 7 9 < = >?
Niech { ; G 1 , G 2 ,..., G F }
L W J ` R X MR
T N K Y ^ UL N P ]L T R Q Z N X MN
sa b
ÿ
% 0 ,
þ
ÿ
*
ÿ
, ze
þ ÿ ($ ) C D E
MT N U V W R X Y Z [
(c ) →
d
V K W L V UV W R \
L N
W ]^ _ Q Z L Y X X MP MN S
( c ) zdefiniowane jako
g
k
(i ) = f
h
dla wszystkich
v p
n
∈
m
u q v y y z zp {
(l )
o p qr
v u | } x y zx
n
, ∈
m
s w p s y
n
y r
W
s t u v s ws u x y zp
{ 0 , 1 ,..., ,...}
qr x p s
∈
m
u
w v p qr w v p y z
w x r x z
H(X),h)
n
( ( ),
n
( )) ≤ ⋅ ( , )
(12.5)
(l ) .
s y zp u x }
v u | } xo ~ {
s. Zatem
w u y {
(12.4)
(i )
h
=1
s t u v s ws u x y zp {
dla wszystkich
j
o p qr
v u | } xo ~ p
v x p } y s z~
(l )
t x
w p w p y o y ~
r w o p qr o p t y {
t s u s y p s
+1
=
w s v u z~ v x y zp {
( )
0
∈
m
o p qr v zp } y
(l )
t s
z~
w x y z
-
w u y x y zx
Punkt
¡
¢
£ ¤ ¥ ¦ § ¨
© ª « ¬ § ¦
=
§ ¦ © ®
(
)=
=1
¯ ° ª ± ²³¯ ¬ ± © ¯
(
).
´ ªµ ± µ
(12.6)
® ° ¶ « ¥
· ± ª ¯ ¸ « ¬ ¨ § ¹
¯ ¥ ¸ µ ¯ ª¯ ¸ « º
µ ¸ ¤ » «¼ ¦ § ¨ § ¹
¬ « µ ¨ ¸ « ¬ ¨ ¼ ± ½ ·
ªµ ± ° ½µ · «¶ § ± ¬ ±
Á
« ·ª « ° ·¯ ª ¥ ® » ¯
´ ¯ ¾ ¯ § ¨
£ « ª ¥ µ ±¼
´ ªµ ± ° ½µ · « ¶ § ± º
Ç È É Ê Ë Ì Í Î Ï Ì ÐÑ Ò Ó Í Ô
Ã
³® £ ¼ ± © ¯
± ³±
« ·ª « ° · ¯ ª ± ¾
¼ ± ½·
W
µ ¶ ¯ » ¯ ¬ ±
¥ ± · ± ª ¾ ¬ ½·¨ § µ ¬ ¨ ¾
¯ ¥ ¸ µ ¯ ª¯ ¸ « ¬ ± ¾
¯ £ ± ° ·¨ À
Ã
µ ¸ ¤ » «¼ ¦ § ¨ ¾
´ ª « ° ·¨ § ±
ÄÅ Æ
¿ª « ° · « ³± ¾ À
¾ ¯ © ¦ § ¨ ¾
¥ ± ¿¬ ¯ ¸ « ¬ ¨
¸ ¨ © ± ¬ ± ª ¯ ¸ « Â
¼ ± ½·
¬ «¼ § µ ¤ ² § ±¼
¼ « ° ¯
´ ªµ ¨
« ¿¬ § µ ¬ ¨ § ¹ À
ÑÕ Ö × Ö Ó Ì × Ø Ó Ù
¿ª « ° · « ³ ¾ ¯ » ¬ «
§ µ ¤ ² § À
³® £
ªµ ¨ ° ¶ « ¥ ¯ ¸ ¯
¸ ¨ © ± ¬ ± ª ¯ ¸ « Â
·ª Ú¼ ° ¦·
Á
Ûß Ü ¢ àß á Ý ¾ ¯ » ¬ « ¸ ¨ © ± ¬ ± ª ¯ ¸ « Â
µ «
´ ªµ ¨
´ ¯ ¾ ¯ § ¨
Æ ± ª´ º ½° ± © ¯
´ ¯ ¾ ¯ § ¦ ·ªµ ± § ¹
245
¯
´ ª µ ± ° ½µ · « ¶ § ± º
¸ ± ªµ § ¹ ¯ ¶° « § ¹
¯ ´ ± ª «·¯ ªÚ ¸
¸
« ¿¬ § µ ¬ ¨ § ¹
´ ® ¬ ° · « § ¹
¥ µ « ¶ «¼ ¦ § ¨ § ¹
¬ «
¬ «
¯ £ ª « µ ±
Û Ü ¢Ü Ý ¢ ÛÞ Ü Ü ¢Ü Ý
§ « ¶¨ ¾
¯ £ ª « µ ± â
ä
ä
ä
ªµ ± ° ½µ · «¶ § ± ¬ «
Á
¸ µ ¯ ª ± ¾
¯ ´ ± ª «·¯ ª «
ã
1 Ø
ã
0.5 0 0
= 0 0.5 Ø + 0 ,
ã
2 Ø
ã
0.5 0
= 0 0.5 Ø
100
+ 0 ,
ã
3 Ø
ã
0.5 0
= 0 0.5 Ø
20
+ 74 .
© ± ¯ ¾ ± ·ª¨ § µ ¬ ±
¥ µ « ¶ «¼ ¦ § ± © ¯
¬ «
½¶® » ¦ § ±
¥ ¯
© ± ¬ ± ª « §¼
å
ä
£ ¨
© ± ¬ ± ª « ·¯ ª
µ ¶ ¯ » ¯ ¬ ±
£ ¨ ¶
¼ ± ¥ ¬ « °
¿ª « ° · « ³¬ ±¼
¸
Ø
å
= Ó
½° « ³
µ
° ¯ ¾ ´ ª ± ½¼
° ¯ ¬ · ª « ½· ± ¾
gdzie k - kontrast, a j ì ³¯ £ « ³¬ ¨
½µ « ª ¯ ²§ £ ¤ ¥ µ ±
µ « ´ ½ « Â
å
Ø + Õ .
¬ « ³ ± » ¨
ªµ ± ° ½µ · « ¶ § ± ¬ ±
½¦
¥ ¨ ½° ª ± ·¬ ¨ ¾
â
¥ ¯ ¥ « Â
·¯
Á
µ « ½· ¯ ½ ¯ ¸ « ¬ « § ¹
¸ ¨ ° ¯ ª µ ¨ ½·¨ ¸ « ¬ ±
¬ «
(12.6)
¥ ¯
¾ ¯ » ±
´ ª ¯ ½· ±
µ £ ¯ ªµ ±
µ ¥ ± ¿¬ ¯ ¸ « Â
½° ¯ ¬ ½· ª® ¯ ¸ « ¬ ± © ¯
´ ªµ ¨¼ ¾ ¯ ¸ « Â
° ¯ ½µ · ¯ ¸ ¬ ¨ § ¹
¿® ¬ ° §¼ ¤
À
é
ê
µ « ´ ½
¯ ´ ± ª « ·¯ ª «
µ
´ ªµ ± ° ½µ · «¶ § ± ¬ « ¾ â
£ « ª ¥ µ ¯
¯ £ ³§ µ ± ¬ ¯ ¸ ¯
ª¯ µ ¸ ¦ µ « ¬ «
¸ « ª· ¯ ² §
Σ( s ) = a n s n + .... + a1 s + a 0
¼ « ½° ª « ¸ ¯ ²§ ¦
· « °
¿® ¬ ° §¼
¿® ¬ ° §¼
¯ » ¬ «
¼ « ½¬ ¯ ²§
° ¯ ª µ ¨ ½· «¼ ¦ §
¼ « ° ¯ â
Ï
Σ( ) =
¼ « ½° ª « ¸ ¯ ²Â À
¾ « § ± ªµ ¯ ¸ ¨
¯ © Ú ³¬ ¨ ¾
Í
ã
® » ¨ · ± § µ ¬ ¨ ¢
½µ « ª ¯ ²§ À
wielomianowej Σ : R → R
¸ ½´ ¯ ½Ú £ ¬ « ½· ¤ ´ ® ¼ ¦ § ¨
danego obrazu S
¾ ¯ ¥ ± ³®
¾ ¯ » ¬ «
å
å
æ
´ ª « ° ·¨ § µ ¬ ¨ § ¹
¥ µ « ¶ «¼ ¦ § ±¼
·¨ ´ ¯ ¸ ± © ¯
å
ç
Ñ
ã
£ « ª ¥ µ ±¼
´ ªµ ± ° ½µ · « ¶ § ± ¬ ±
´ ¯ ½· « § ± ¢
« ³© ¯ ª ¨ · ¾ Ú ¸
¿ª « ° · « ³
¿ª « ° · « ³«
¯ £ ª « µ ± â
å
è
¯ ´ ± ª «·¯ ª « ¼ ± ½µ § µ ±
(12.5)
© ± ¯ ¾ ± ·ª¨ § µ ¬ ¨ ¾
ë
Î Ï
µ
+ ,
½° « ³
½¤ ¸ Ú ¸ § µ « ½ ¸ ¨ ª « » «¶ ¬ « ½· ¤ ´ ® ¼ ¦ § ¯ â
å
å
ä
Ø
Ï
ã
å
å
ç
Ñ
å
= Ó
0
Í
0
Ø
0å
Î
Ï
+ Õ
ë
ã
å
æ
0
.
å
å
(12.7)
12.3. Konstrukcja dowolnego obrazu przy pomocy lokalnego IFS
´ ¯ ½Ú £
Tak prosty s
¸ ¨ ° ¯ ª µ ¨ ½· « ¬ ¨ ¸
» ±
® ¥ «
¬ « ¾
½¤
¯ ° ª ± ²³± ¬ «
´ ª « ° ·¨ § ± ¢ ¼ ± ¥ ¬ « °
· « °
µ ¥ ± ¿¬ ¯ ¸ « Â
ª « §¼ « § ¹
kolejnych
ite
´ ªµ ¨ ´ « ¥ ° ® £ « ª ¥ µ ¯
´ ª ¯ ½· ± © ¯
¥ ¯ ¸ ¯ ³¬ ¨
¬ ± ¾ ¯ » ³ ¸ ± À é
® ½« ¶£ ¨
¯ ¬
¾ ± Â
¥ ¯
£ ¨ ¶ ¯ £ ¨
· ¯
¿ª « ° · « ³¬ ¨ § ¹
° ¯ ¾ ´ ª ± ½¼ À í ª ® ¥ ¬ ¯
¿ª « ° · « ³¬ ±
¸ ± ª ¬ ±¼ ½µ ¦
¬ « ·® ª « ³¬ ¨
£ ¯ ¸ ± ¾
¯ £ ª « µ Ú ¸
§ ± ³Ú ¸
§ ¯ ª « µ
¯ £ ª « µ ®
¯ £ ª « µ
¬ ±
´ ªµ ± ° ½µ · « ¶ § ± ¬ «
® µ ¨ ½° « ¾ ¨
© ± ¬ ± ª® ¼ ¦ § ± © ¯
© ± ¬ ± ª « ·¯ ªÚ ¸
´ ¯ ´ ª µ ± µ
´ ¯ ½· « Â
¾ ¯ » ± ¼ ± ½µ § µ ±
¼ « ° ¯
« ·ª « ° ·¯ ª
¸ ¨ ª « î ¬ ±
§ ± § ¹ ¨
¾ ¯ » ±
£ ¯ ¸ ± ¾
ÄÅ Æ ¢ » ±
¸ ¨ ¯ £ ª « µ Â
´ ª µ ¨
¼ ± © ¯
° ¯ ¾ ´ ª ± ½¯ ¸ « ¬ ± © ¯
¾ ¯ » ³ ¸ ± ¢ ¼ ± ¥ ¬ « °
´ ªµ ± ° ½µ · «¶ § ± ¬ «
£ ¨ Â
¶ « ·¸ ¯
½¯ £ ± ¢
´ ¯ ¾ ¯ § ¨
¯ £ ª « µ ® À
µ £ ® ¥ ¯ ¸ « ¬ ±
µ ¸ ¤ » «¼ ¦ § ± © ¯
¸
Ã
ÄÅ Æ
¼ ± ½·
½« ¾ ¯ ´ ¯ ¥ ¯ £ ± º ½·¸ « À
Lokalny iteracyjny system funkcji
£ ¨
½° ¯ ¬ ½· ª® ¯ ¸ « Â
è
´ ¯¼ ¤ § « ÄÅ Æ À Æ ° ¯ ª ¯
ª « µ
µ
¬ ±
° ¯ ¾ ´ ª ± ½¯ ª
½´ ¯ ½Ú £
¥ ¯ ¸ ¯ ³¬ ¦
¿ª « ° · « ³¬ ¨
½° ¯ ¬ ½· ª® ¯ ¸ « Â
¥ ¯ ° ¶ « ¥ ¬ ¯ ²§ ¦ ¢
´ ¯ ·ªµ ± £ «
¯ £ ± ° ·®
·¯
¥ ¯ ° ¯ ¬ « Â
´ ± ¸ ¬ ± © ¯
½« ¾ ¯ ´ ¯ ¥ ¯ £ ¬ ± © ¯ ¢ ° · Ú ª ¨
·ªµ ± £ «
µ ª ± « ³µ ¯ ¸ « Â
ª ¯ µ ½µ ± ªµ ± ¬ «
£ ¤ ¥ µ ±
° ¯ ¬ § ± ´ §¼ ¤
´ ª µ ¨ £ ³» « ¶
´ ªµ ¨ £ ³» ± ¬ «
dany ob
odpowiednio prostych fragmentów obrazu innymi podobnymi fragmentami tego samego
246
¯ £ ª « µ ® ¢
° ·Ú ª ±
¿ª « ° · « ³¬ ± © ¯
í « ° ´ ¯ ¾ ¨ ½¶
ï ÄÅ Æ Ý ¢
¸ ¨ ½· ¤ ´ ® ¼ ¦
¾ ® ½
µ ¯ ½· « Â
ª ± « ³µ ® ¼ ±
° ·Ú ª¨
¸
¬ ± ¾ « ³
³¯ ° « ³¬ ¨
° ¯ ³±¼ ¬ ¨ § ¹
¯ ´ ½ « Â
° « » ¥ ¨
¯ £ ª « µ ® ¢
¥ ± ¦
· ± ª « § ¨ ¼ ¬ ¨
§ ¹
¬ «
µ ¯ ª¯ ¸ « º À
¯ £ ª « µ ¢
ª ± ´ ª ± µ ± ¬ · « §¼ ¤
° « » ¥ ¨ ¾
¯
· ± ª « §¼ « § ¹
½µ · «¶ § ± ¬ ±
obrazu
i przek ¯ ¥ ¸
µ ¥ ± ¿¬ ¯ ¸ « ¬ ¨ § ¹
¸
ª ¯ µ ½µ ± ªµ ¯ ¬ «
½¨ ½· ± ¾
¿® ¬ ° §¼
´ ªµ ¨ £ ³» «
¬ ¯ ¸ ±
Ã
¯ £ ª « µ ± À
· ± ¬
Ä ¥ ± «
¸ µ «¼ ± ¾ ¬ ± © ¯
¯ £ ª « µ
«
´ « ª « ¾ ± ·ª¨
· ± © ¯
¬ «
´ ¯ ¥ ½· « ¸ ±
° · Ú ª ±¼
· ± © ¯
¾ ¯ » ¬ «
µ
¯ ´ ½®
´ ¯ ´ ªµ ± µ
½· « ¬ ¯ ¸ ¦
¾ ¯ » ¬ «
¯ £ ª « µ ®
³® £
½¨ ½· ± ¾
-
¿ª « © ¾ ± ¬ · Ú ¸
´ ªµ ¨
¸ ¤ ° ½µ ¦
´ ¯ ¾ ¯ § ¨
½° ® · ± § µ ¬ ¯ ²§ ¦
¼ ± ¥ ¬ ¯ µ ¬ « § µ ¬ ±
µ ª ± ° ¯ ¬ ½· ª® ¯ ¸ « Â
¯ £ ª « µ ® À
¿® ¬ § · ¯ ¬
´ ¯ £ ª « ¬ ±
½« ¾ ± © ¯
¾ ¬ ±¼ ½µ ¦
¯ £ ± ° ·®
¿ª « © ¾ ± ¬ · Ú ¸
Û « ¬ © À ³ ¯ § « ³ · ± ª « · ± ¥
¥ « ¬ ¨
¿ª « © ¾ ± ¬ ·¨
½´ ¯ ½Ú £
½ « ¾ ¯ ´ ¯ ¥ ¯ £ ± º ½·¸ «
´ ¯ ¥ ¯ £ ± º ½·¸ «
¥ ± ° ¯ ¥ ¯ ¸ « ³¬ ¦
¯ £ ª « µ
µ
£ « ª ¥ µ ¯
¥ ® » ¦
¥ ¯ ° ¶ « ¥ ¬ ¯ ²§ ¦ À
å
Ý £ ¤ ¥ µ ±
µ ¸ « ª· ¦
Definicja 12.5. Niech (X,d å
å
ð
ä
podzbiorami X. Niech
→ñ
å:
¸ ½´ Ú ¶ § µ ¨ ¬ ¬ ° « ¾ µ ¸ ¤ » « ¬ « Ï
. Wtedy
£ ¤ ¥ ¦
å
ä
{
µ ¸ « ¬ ± ¼ ± ½·
³¯ ° « ³¬ ¨ ¾
ò ¯ ·¨ § ¹ § µ « ½
¬ «
° · Ú ª¨ ¾
ÄÅ Æ ¢ «
¯ ° ª ± ²³¯ ¬ ¨
µ £ Ú ª
ð
Ö
×
, = 1,..., niepustymi
´ ª µ ± ° ½µ · « ¶ § ± ¬ « ¾
¸
Û
X,d) ze
³¯ ° « ³¬ ¨ ¾
ð
:
¸
Ö
→ñ ,
×
= 1,..., }
½ ´ Ú ¶ § µ ¨ ¬ ¬ ° ± ¾
´ ª ± µ ± ¬ · ¯ ¸ « ¬ ¨ § ¹
µ ¯ ½· «¶
¾ ± ·ª¨ § µ ¬ ¦ ¢ «
å
³§ µ £ « ¼ ± ½ ·
¥ µ ± ¥ µ ¬ ¦
´ ª µ ± ½· ª µ ± ¬ ¦
¸ « ª·¯ ²§
´ ªµ ± µ
¬ « ½
¿® ¬ ° §¼
(12.8)
µ ¸ ¤ » « ¬ «
ï ÄÅ Æ À
´ ªµ ± ° ½µ · «¶ § ± º
¼ « ½¬ ¯ ²§ À
£ ¨ ¶ «
ò µ « ¶ « ¶ ¨
§ « ¶ ¦
¸ ¤ §
´ ª µ ± ½· ª µ ± º ¢
¯ ¬ ±
¬ «
§ « ¶ ¨ ¾
obrazie. W
definiowaniu lokalnego iteracyjnego systemu funkcji zachodzi jedna podstawowa
¥ µ ± ¥ µ ¬ ¦ ´ ¯ ½µ § µ ± © Ú ³¬ ¨ § ¹ ´ ª µ ± ° ½µ · « ¶ § ± º ¢ µ ° · Ú ª¨ § ¹ µ ¶ ¯ » ¯ ¬ ¨ ¼ ± ½· ï Ä Å Æ ¢ ¬ ± ¾ ® ½ £ ¨ Â
zmiana
§ « ¶¨
¯ £ ª « µ À
Æ ¦
¯ ¬ ±
¥ ± ¿ ¬ ¯ ¸ « ¬ ±
³¯ ° « ³¬ ± À é ¬ ±¼ ½ µ ¨
¬ ¯ ²¬ °
´ ¯ ½µ § µ ± © Ú ³¬ ¨ § ¹
¯ ¥ ¸ µ ¯ ª¯ ¸ « º
µ ¸ ¤ » «¼ ¦ § ¨ § ¹
¯ £ ¯ °
Ûµ « ¾ « ½·
¯ ° ª ± ²³± ¬ «
ï ¯ ° « ³¬ ¨
ó ± » ± ³
§ « ¶ ± © ¯
¯ £ ª « µ ® Ý
¸ ½´ ¯ ¾ ¬ « ¬ ¨ § ¹
ÄÅ Æ
½¦
¾ ¯ » ±
¬ ±
« ·ª « ° ·¯ ª « ¾ ¢
A i B ½ · ¬ ± ¼ ±
½´ ª « ¸ « ¢
´ « ª « ¾ ± ·ªÚ ¸
¾ ± Â
· ¯
« ·ª « ° ·¯ ª « ¢
· « ° » ±
ð
ô
∪
« ·ª « ° ·¯ ª ¢ ·¯
¬ « ¼ ¸ ¤ ° ½ µ ¨ ¢ ·¼ À · « ° ¢
° · Ú ª¨
¸ ¤ ° ½µ ±
· ± ¯ ª ±·¨ § µ ¬ ±
½¤ ¢
½µ § µ ± © Ú ¶¨
¬ « ·® ª « ³¬ ¨ § ¹
¾ «
¸ ½µ ¨ ½· ° ±
» ±
¸ ¨ ¥ «¼ ±
¬ ± µ £ ¤ ¥ ¬ ±
¥ ¯
´ ± ¶ ¬ ± © ¯
µ ¥ ± ¿¬ ¯ ¸ « ¬ «
´ ªµ ± ° ½µ · « ¶ § ± º ¢ · « ° » ±
£ ¦ ¥ î
¼ ± ½·
¾ ¯ » ±
§ ± § ¹ ¨ ¢
¬ «
¼ « ° ¯
¼ ± © ¯
ï ÄÅ Æ
´ ¯ ·ªµ ± £ «
¬ ¯ ²¬ ° « À
¸ ± ³±
§ ¯
¸ ½µ ¨ ½· ° ±
ï ÄÅ Æ
£ ¨
¾ ± Â
« ° · « ° ·¯ ª ± ¾
µ « ¸ ± ª «
» ±
§ ¹
ª Ú » ¬ ¨ § ¹
¯ µ ¬ « § µ « ¢
« ·ª « ° ·¯ ªÚ ¸
» ±
¼ ± ²³
´ ¯ µ ¯ ½· «¶ ± À õ ±
¬ « ªµ ¤ ¥ µ ±
´ ¯ ¥ ½· « ¸ ±
¸ § ¹ ¯ ¥ µ ¦ §
¾ ¯ ¥ ± ³¯ ¸ « ¬ «
° ¯ ¬ ½· ª® ¯ ¸ « Â
À
½· ¬ ±¼ ±
¸
¯ £ ª « µ Ú ¸
´ ª « ° ·¨ § µ ¬ ±
algorytmy kompresji.
12.4. Algorytmy praktyczne
ö
÷ ø ù ú û üý þ ÿ
ÿ
øù
üý
ú
ÿ
÷ øù ú
ú
ø
üù ý þ
ù ÿ þ
ú
þ
þ
ÿ
ø þ
ý þ
÷
ú
ÿ þ
û
ù þ üþ û
û ú
÷
ù þ
ù
ø
ú ÷
þ
þ
ú
û
ù
ÿ
ø
û ú ø þ
û þ
obrazowych.
Elementarny
schemat
fraktalnego
kompresora
i dekompresora
przedstawia
ø
ü
ú
þ
ÿ
û þ
ù ý ú
ø
ü
û ú ø
ø þ
ý þ
ú üý ü
ú
ú ü
ú ýø
ù
ø
ú ü
ÿ
þ
þ
û
ø ú
÷ ø
þ
û ú
÷ ø ú ü
ù
ù
ù
ù þ
û
ú
ý þ
üý ø
ú û
ù
þ
ø
ú üý
û ú
û
ÿ
÷
ú
÷ øù ú
÷ þ ø þ
ú ýø
÷
ú
ù þ
ÿ þ
üù
ú
þ
ÿ
þ
÷ øù ú
ÿ þ
ÿ
ú
ú
÷
ø
ù
ù
üù
ú
üý
ÿ
þ
ú
þ
ý ú ø þ
þ ø û ù
ü
þ üý
û
þ
÷ øù
þ
÷
ú
ú
÷
ú
ú
÷
ÿ
ý ú
ú
ú
ø ú
ý
ø ú
÷
þ
ÿ
ø
ù
ú
û
û
û ø
ý ú ø
÷ þ ø þ
ú ýø
þ ý
ù
ø þ ù
ý ú
û
üý þ
÷
ÿ
ú
û ú
ú
ù
ý
ÿ þ
ù þ ü
ø
û ù
ÿ þ
ù
ý
þ
ÿ
ù
ÿ þ
þ
ø þ ù
laþ
÷
ÿ
û
ú ø
÷ ø ú ü
ø
þ
ú û ù
ÿ
þ
û ÿ ù
üýÿ þ
ú
û ù
üý ø
ù þ ü
÷
ú
ù þ ü
ù ø ú
ú
ø þ ù
÷ øù ú ù
û þ ú
û
247
üý
û û þ
kolejnym podrozdziale.
þ ø û ù
ÿ üù
ú û
ú û
ú
ü÷
÷ øù ú û ú
üý þ ú
þ üý
ø ú
üù ý þ
þ
ú û ù
ÿ
ÿ û ù
ú
÷ øù ú û ú
þ ø û ù
÷
ú
ú
ÿ
KOMPRESJA
Obraz
oryginalny
0
1
5
:
8 3
=
2 3
2
;
>
45 6
3
4;
4?
2
1
7
2
3
3
4;
8 5 3
4
:
9
2
Konstrukcja
LIFS
4
<
3
4
:
<
?
Zakodowana reprezentacja obrazu
Kodowanie
@ A B >
41 ?
;
C
1
strumienia
parametrów
DEKOMPRESJA
Zakodowana reprezentacja obrazu Dekodowanie
strumienia
parametrów
Obraz
zrekonstruowany
Generacja
obrazu jako
atraktora LIFS
Odtworzenie
LIFS
Rys. 12.1. Podstawowy schemat kompresji i dekompresji fraktalnej obrazów.
ù þ
Przy konstruowaniu LIFS bardzo istotnym
û
þ
ù
ü
þ
ú
ù
ø
ý ú
zdefiniowanego dla i -
÷
û
ú
þ û ý
þ
ø
ÿ þ øý
ý
ú øù
üýÿ þ
þ
ÿ
(
ú
ú
þ
przez Gi
÷
û ù
÷ øù ú
þ
ü
ÿ
ø ú
)
ø þ ù
þ ø
þ
þ
ø
÷ øù ú
ú
ù
ù
= max det
+
!
i
þ ø
ÿ þ ø
ú û
÷
ø
ü ý þ ú
û üý þ ÿ
ýøù
*
þ
ü
ÿ
û ù
þ
ú
ú
þ
ý ú
ÿ
ú üù
ý
÷
ù
ý ø þ üý
ú û ù
ÿ ú
ù
þ ø û ù
÷
ý
üù ý þ
ú
ÿ þ øý
ù ø
ú
û
ù
þ
÷ þ ø þ
ÿ þ ø
þ
ù
ÿ ú û
#
÷
þ
ÿ
ú
û
&
'
÷
ø þ
ý
ÿ
þ
þ
÷ øù ú
þ
#
þ
û
ø ú û
÷ ø ù ú û üý þ ÿ
ú üý
þ üý
÷
ù ÿ
üù ý þ
ú
ù
$ %
ø
þ
þ
þ
þ
!
"
ù
,
þ ø
&
ø þ ù
bi
, a przez
d i
ú
ú ÿ þ ø
üý þ
÷ ø ù ú üý ø ù ú
û ù
ø
÷
ú
ÿ þ û ø þ ý
(
ý
wþ prz
ø
ü
ù þ
ÿ ú
ú
+
ú
ù
ú
þ
ú
ø þ ù
þ
ÿ þ ø
ù ÿ
ú üý ù þ ÷ ú ÿ
a
Gi = i
ci
ø
þ
ú û ù
÷
ú û ù
⋅ ( ⋅ π )1 / η < 1 ,
ù ø
üù ý þ
ú û
þ
û
ú
% *
(12.9)
.
-
÷ øù ú
ú üù
øù ú
ù ú
þ üý
ú üý
þ
!
ù
ú û ù
,
gdzie k = max k i ,
ú
ÿ û ù
û ù
üý þ ý ú
ÿ û ù
ú ýø
÷ øù ú
þ
û
ü
ÿ þ
ú
ú
ø
ú û ù
üù ý þ
û ù
û ÿ ù
þ û
ù ÿ
ú
þ
û
ú ýø
ú
ù
þ
û
ú üý
ù
ú
ù
ø
ÿ
#
ú
#
ü
ÿ ù
þ
ÿ þ
ú
û
ÿ þ
ú
ú
÷
ú
þ
üý þ
%
þ û
þ
ÿ
ù
ù þ
ú
ý ø þ üý
248
þ
. %
þ
*
û ÿ ù
(
ø
/
ÿ þ
4,
ù
ÿ
ú ü ù
þ ø
üý
ÿ
û
kη ⋅ d ⋅π < 1,
ú ýø
&
= 2, d=0.5
1
k<
. W
2
D
E F G H I
J K L I
J M
E N
K O
k ∈ [0.5;0.7]
przekraczaniu wa
T
\
P Q K F L
H U ]
^
P F
N \
J M
D
P U E F
E K I R
V P W
G
S
T R
U
N L H E F
V P W
V H
^
[
V D
N
V ` \
D
N
D E F O
J K
F
D
W
N
V H N
V K
V H F X Q
J K U _
`
L
[
E H N
Y J P
S
F G
V I
S
F
L
U R
O
I
L
O
I
F E H N
J M
N
Y Z
^ O
G
N L H E F V H T
K N E N O
F a
D
k z zakresu
F S
P W H F R
Q J
N
L
P U
[
P G
F R
Q J
U R
K
O
F E T
L
G T
K O
W ]
F L
P F
b
c
K I
V G
F L
F
O
G
N L
P U J K
H U L
[
F
^ N
D
F V N O
F L
P F
\
N G
` O
S
N ]
U
L
P U
\
I
Z
V G
N
S
D
U L
V N O
F L
F
D
E K U K
L
N
Y Z
[
D
E K
U G
F K F L
P F
^
N
^
F H G
O
P Q K
praktycznych roz
K \
P `
E
H I
D
N O
I
J M
N O
O
U _
F L
F E H N
N
V H E T
P F J M
Y J P
T
N \
S
D
P U L
E F
V K
E N H ` O
P F
J K
^
F
e
F L I
V P W
T
J M
K
E ` O
V H E K F L I
L
O
P U ]
J M
N
F E H N
G
^ \
N
^
Y J P F S
N O
P Z e
F L
P H D
P
k i do dekompresji. W
P U
b
N \
P
T
E N H ` O
S
P U
V K
^
J K F R
U d P L
Q J
P T R
Q J
O
D
V H E T
U O
S
P U
P U L
L
P T
[
O
I R
Y J P N O
I
S
R
U ^ I
L
P U
P L
^
U G
K \
Przekazane do kodowanego
\
N
G T
E K
U G
D
E K U J P O
^ K P U ^ K
P L
I
T
V I
H I
P N E T
J M
O
I
_
K L
U N
S
F J K N L
U H E I
U
O
J K L I
F E H N
J M
Y J P
D
H E F L
E K U G
V
V K H F X J U a
F J R
P
P
R
F V G
P K N
E F O
N
S
U H E I
Y J P
^
[
K T
D
U X L
P F R
Q
P L
d N
E S
F J R
W
K F O
F E H Q
O
F
J K
G
L I
F ] ^
J M
U _
b
N
[
O
F E H N
Y J P
G
N
L H E F V H T
P
P L
^
U G
P
D
V P U
[
D
j
I
V K H F X J U a
V b k l
bl
b
m
_
E K I
U N
S
U H E I
G X F ^
D
N
J K
G
L I
E I
J M
J P F
e
V X T
^ K
]
P U ^
Q J
^
K P L
I
N
^
U d P L
K
P N O
K F J M
N
F L
P F
f
^ K Q J I
g h
S
P
i
L
O
F
^
U G
V P U \
N
^
P U
U E K U
\
N
G
b
F S
P
E N
K D
P W H I
S
E K
I
T
\
[
D
N
S
N
J I
T
G
N
Y L
P U
J K H U E U J M
V P F H U G
D
E K U V T
L
P W H I
J M
O
K _
W ^
U S
V P U \
P U
N
D
N X N O
W
V K
U E N
G
N
Y J P e
O
I
V N
G
N
Y J P
[
G
` X G
D
–
P U S
L
N X N O
W
V K
U E N
G
N
Y J P
N
O
I
V N
G
N
[
Y J P
\
N G
T
b
^
D
N
m
E K I
G X F
^
N O
I
D T
L
G H
N
K L
F J K
N L I
V K
F E I
S
[
F
U ] I
^
N
J K H U E U J M
\
N
[
J P Q _ X Q
P
G
` O
D
N
G
E I
J P F
n N
^
V H F O
N O
U R
V P F H G
P
K
F K L
F J K N
L
U R
_
E T
\
Q
P L
[
E F K
N
^
V P F H U G
E I
V N O
P Q
[
F L I
J M
J P U a
V K Q
P L
P Q
G
E N D
G
N O
F L
Q e
G
E U V G
L
U _
F
-kropka i kreska –dwie
[
kropki).
m
E K I
G X F ^
D
E F G H I
J K L
U _
N
F
_
N E I H S
T
G
N
S
D
E U
V N
E F
d E F G H F
[
K L
F
J K
Q J Q
U d U G H I O
L
N
Y Z
G
N
L
P U
S
D
E U
VR
N
D
N
K O
F
[
P
D
E K U ^
N
S
V H F O
P F
E I
V
b
k l
bo
e
F
F R
Q J U _
N
T
K I
V G
F
Z
[
V J M
U S
F H
F
_
N
E I H S
T
^
U G
N
S
D
E U
VR
P e
[
N
^ H O
F E K F R
Q J U _
N
P H U E F J I R
N \
E F K
G
D
E U
V N O
F L
I
D
E K U ^
V H F O
P F
E I
V T
L
U G
k l
bp
b
12.5. Optymalizacja algorytmu kompresji fraktalnej
m
N
^
V H F O
N O
I
V J M
U S
F H
G
N
S
D
E U
E U Y
N
L
Q
^
N G X F ^
VR
P
d E F G H F
L
U R
R
U V H
J K
F V N
J M X N
L
L I
b
Wyznaczanie LIFS
[
D
E K I
\
P ] F R
Q J U _
N
N \
E F K
K
N
G
[
D
E K
D
F E F S
U
D
N
L
N
Y J P Q
D
N
J P Q _
F
K
G
P O
F L
U H E T
R F
P F
\
V L
N
N
G
` O
F
^ K
L
F
P U ^ K P L
V H W D
L
I
P U
e
N \
N G
E U
E F J F L
Y
F L
P F
P F
H I
N
^
[
G
G
P O
F L
P T
L
F R
U D
V K
U R
F D
E N
G
V I
N
^
J M
\
U _ X N
Y J P
N G
N
Y J P
N \
E F K T
S
F
J R
P
N
P U J K L
N
Y Z
O
P U
D
N
G
E N H L
U _
N
N
G
E U Y
F L
F ]
^
U _
N
P F
N G T
D
N G T
D H I
S
b
m
E K I
G X F ^
N O
q
s
N
F
L
U _
N
[
E K
U J P
[
\
N
[
\
G
N S
wdziedziny, w
E K I
D
N
S
N
J I
F
_
N
E I H S
T
H E F L
V d N
E S
F J I R L
U _
N
K
r
H E O
F X F
D
E U
N
G
VR
F
N X N
Y E U ^
V U G T
L
L
P U R
^ I
e
[
J K F
V
H U J K L
^ I
P
^
[
G
_
^ I
S
U H N
N
^ N O
^
Q
d E F G H F
L
Q e
L
F
H U R
V F S
U R
N
Y Z
G
F L
P F
L
P U
R
S
F
V K I
L
P U e
G
P
d P G
F J R
P
K
N
V H F X N
D
E K U ^
V H F O
G
F
S
P L T
H b
m
N L
F ^ H N
[
U
V H
D
E K U G
N L T R Q J F
algorytm optymalizacji, zarówno w sensie RS
` O
N
[
V G T
N L
[
[
D
G
[
Y J P e
[
P U
Q
[
[
O
V N \
[
V K T
V K T
F
P N
L
I
J M
O
^
F
V K
O
q
U R
O
R
F G
P W G
P
V K
J K
N
Y J P
F V T
G
K
F
N
S
V H N
V N O
D
VR
E U
F a
b
u
P
P b
t
G
[
J K
[
249
W Y J P
H U _
N
D
N
^ E N
K
^ K
P F X T
b
I
F
S
D
uzyskiwania
F _
E K I
F
O
G X F ^
P W J
N O
H U L
I
J
M
Start
m
N
^ K P F X
m
N
D
E K U J P O
^ K P F X
^
K
^ K
P U ^ K P L
P U ^ K
P L
I
I
P
D
Pobranie kolejnego bloku P
Ustawienie minimalnej
min = ∞
N
^
U _ X N
Y J P
\
[
N
G
v
` O
[
Pobranie kolejnego bloku D
m
E K U G
V K H F X J U L
P U
geometryczne bloku D
Wyznaczenie parametrów
chromatycznych
n G
N
L H E F
Obliczenie d
N
^
S
P W ^ K I
\
N
G
V H e
U _ X N
R
F
V L
Y J P
F S
P
DiP
T
d<
Y Z w
[
[
v
N
x
F D
F S
P U H F R
P K N
S
U H E P W
i
parametry chromatyczne
min ?
N
T
x
N
V H F X I
N
x
izometrie?
N
V H F X I
T
bloki D?
T
N
Zapisanie izometrii bloku D
na P i parametrów
chromatycznych
x
N
V H F X I
bloki P?
N
Stop
Rys. 12.3 Schemat blokowy fraktalnej metody kompresji.
250
Start
Czytanie parametrów
p
LIFS
®
Inicjalizacja obrazu
przeciwdziedziny P
¯
¢
°
Tworzenie obrazu dziedziny D (dowolny obraz
P poprzedniej iteracji)
«
¦
¢
±
bloku D na blok P
T
Z
¢
-
³
N
T
²
iteracje?
N
Stop
Rys. 12.4. Schemat blokowy algorytmu dekompresji metody fraktalnej.
y
z
{
|
}
~
¢
¢
¨
z
}
} | ~
¤
§
©
§
¥
¡
¦
§
¥
§
¤
£
¡
¦
£
¢
£
¢
£
¤
¢
¦
¢
£ ¢
£
£
¢
£
¦
¤
algorytmu poszukiwania najbardziej podobnego bloku dziedziny.
ª
§
¢
§
¨
§
¬
§
§
¢
£
§
§
£
¡
§
¢
251
¦
§
¡
¢
§
«
¥
§
¢
ba koniecznych iteracji do rekonstrukcji
£
¥
¢
¥
¨
¢
¢
¬
§
§
¢
§
®
¢
§
£
¢
¢
§
¦
¤
£
¡
¢
¢
¨
«
£
¢
¬
£ ¼
z
½
¾
¢
¿
À
¢
§
¢
¦
¢
¢
£
§
¥
¢
£ ¤
«
¢
º
£
¡ £
£
§
£
¢
§
¨
£
±
£
¨
µ
¢
¦
¡
§
£
§
¨
«
£
§
§
¡
¤
§
§
¢
¥
£
¨
§
-D.
§
§
§
¶
·
¥
¡
¥
§
¢ §
¢
¢
£
¦
£
´ £
¥
«
£
¦
¤
¥
§
¢
¡
§
§
£
¤
¦
£
£ £
£
¢
Á
«
¥
¨
§
¢
Â
§
¦
£
¡
¡
£ ¢
¢
«
¨
Â
£
¢
£
£
¢
£
¡
¡
¢
¢
§
£
§
¥
£
¨
¢
£
¢
¤
£
§
¦
£
¢
¢
¢
¤
¦
¦
§
¤
§
£
§
£
¥
¡
£
£
¢
¥
¡
¥
«
¤
§
£
£
«
£
§
§
¢
¢
¥
¨
¢
¡
¦
¦
£
¤
¢
¡
¢
£ ¢
¢
§
¡
§
¨
¢
«
¤
¯
£
¤ §
¢
§
¥
£
£
¡
© ¹
»
®
¡
§
¢
¨
§
¢
§
£
¢
¸
¢
¡
§
§
¤
§
£ ®
¢
¢
ª
¢
À
¢
¤
¡
£ z
«
¤
±
¥
¨
£
bardzo ograniczonej skute
¢
¦
£
§
£
¢
£
¢
§
§
¢
£
§
£
¢
«
«
§
§ ° ¦
£
§
¨
Akceleracja algorytmu kompresji
Najprostszym rozwi
¢
¢
¢
£
¢
¡
¢
¢
£
§
£ « £
¢
¦
£
£ ¢
«
§
¡
¢
£
£
£
¢
¦
®
§
¢
¢
£
§
¢
§
£
»
§
§
¨
¤
ª
¡
¢
¡ «
§ £
§
¡
¨
Â
¦
£
¦
¢
¢
£
«
¢
Â
£
Ë Ì Í
Î
§
§
«
Ï Ð
¦
Ñ Ò Ó Î
¤
«
Ô
Õ Ö
¨
ª
¨
¬
¤
¨
¤
£
¡
Ê
à Ä
¨ Å
¨
¡
¡
¢
§
£
§
£
Ê
§
£
¢
¥
252
¦
¥
£
£
¢
£
¢
§
§
¢ §
«
§
§
¡
£
§
§
¤
·
-
¨
É
¡
¥
£
£
¤
«
£
§
¨
£ ¨
£
¨
£
¢
¢
¡ £
¢
§
§
£
¦
£
£
«
£
£
¢
§
£
£
¤
§
ci, bloki umiarkowane
§
¢
£
£
¢
®
¢
Trzecia kategoria metod przyspieszania kompresj
¢
ª
¢
¨
¤
§
¤
¤ ¡
¡
¦
£
¢
Â
§
£
¢
£
¨
«
¦
¡
£
¢
¡
§
£ £
£
Innym sposobem jest zmniejszenie
«
«
§
Æ Ç
È ¨
jednolite
«
¤
£
-
¦
£
¨
£
±
£
£ ¥
¢
« §
¥
¢
¦
¢
£
¤
¥
¥
£
¥
¥
¥
¢ ¤
£
¡
¢
£
¨
Blok
danych
Á
Umiarkowany
Jednolity
¨
à Ä
¨ Å
¨
£
£
±
dziowy
Ø
·
Ù Ú Û
§
Ü Ý Þ
ß
à á â à ã
Ú
Ø
£
§
Ù Ú Û
¢
Ü Ý Þ
¢
ß
Mieszany
â à ä
§
à Û
«
Ú
Ø
§
Ù Ú Û
Ü Ý Þ
å
æ
à
ç ä
Ú
kompresji
fraktalnej.
©
Á
§
¢
¡
£
ª
¤
«
¡
¡ £
Á
£
§
£
«
§
¤
§
¦
§
« «
¤
§
£
©
¨
£
§
¤
¤
£
§
£
¢
¦
£
§
¦
¢
¨
¨×
¢
¢
« ¦
à Ä
§
¢
¦
§
¯
¤
§
£
§
£
§
°
£
¦
¨
¨
¨
£
£
¡
¢
najbardziej podobnych bloków jedynie w odpowiedniej klasie czy podklasie, co znacznie
§
¡
¥
£
£
«
¨
Â
§
¡
Wiadomo bowiem,
§
¦
¤
¢
£
¡
¥
£
§
§
¢
£
£
£
253
¥
§
¥
¢
«
¡
¢
®
£
¡
§
±
¥
¨
£
¡
§
£
¢
¤
£
¦
£
¥
§
¥
¨
«
zasadniczo techniki klas
ø
ì í þ
ñ ó
ì ú
ê ö
î
ì ë
ñ
ÿ í ê
ü è
é ê ë
ý û ë
ñ
ú
è
ü
é ê ë
ý ö
ì í î
ê
í î ê
ë
ï
ð ñ ë
ò ó
ô
ñ ó
ñ
õ ö î
÷
ì
ð ì
ø ù
ú
ê û î
ü ø û ú
ê û
í ø
ì ü ö
ë
ñ
ù
ô
ý û
üî
ê
ô
ý ø
è
è
ü
ÿ ý û õ ú
ú
ì î
ù
ê û î
ú
ê û î
é ö
ü ø ÷
ð ì
ú ë
í î
ó
ê
î
ì ý
ì í î
ì ü ú
ñ
ÿ
ì
ñ
ú
ñ ý ù
ÿ í ê
ì ð ú
ð ê í ø
ÿ ý û õ ú
ê û î
ì
ñ
ú
ï
õ ø ê û ð ÷ í ì
û î
ó
ê ì
ï
í ø
è
ú
ð ñ ë
ê
û ý û í þ
ì î ó
ê
ú
ë
í ø
ë ü ø ÷ ü è
ó
ø
ÿ í ê ì í þ
ý ø ì
ì ð û
ï
ú ñ ÿ í ê
ð ñ ë
ë ê
ô
ò ó
ñ ë
ñ
õ
ø
ì ø ö î ÷
ë
ê û ý ö
ú ë ö
ý ì õ ê û ú
ö
arny kolor oznacza
ë
ê û ý ö
ú
û ë
ý ì õ ê û ú
ö
í ø è
ó
ê ÿ í ê û
ì ë
ê
ì ð
ñ ý è
ù
ë
ð ì
ü è
é ê ë
ì
í î
ê
î
û
ü
ú
ê û ø ù
ê û ú
ú
ê í ø è
ó
é ö
ú
ë
í î ê
ñ ï ý ñ
ö
ï
ð ñ ë ö
Bibliografia:
1. M.F. Barnsley, Fractals Everywhere, Nowy York: Academic Press, 1988.
2. A.E .Jacquin, A Novel Fractal block-coding technique for digital images, IEEE Int. Conf.
on ASSP, 1990.
3. J.M. Beaumont, Image Data Compression Using Fractal Techniques, BT Technology
Journal 9(4): 93-108, 1991.
4. A.E .Jacquin, Image Coding based on Fractal Theory of Iterated contractive images,
1(1):18-30, IEEE Trans. on Image Proc., 1992.
5. M.F. Barnsley, and M.P. Hurd Fractal Image compression, Wellesley: AK Peters Ltd.,
1993.
6. W. Skarbek, Metody reprezentacji obrazów cyfrowych, Akademicka Oficyna
Wydawnicza, 1993.
7. B. Ramamurthi, A. Gersho, Classified Vector Quantization of Images, 34(11): 1105-1115,
1986.
254