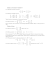+ c - GDR!

1
Dyskretna transformata
falkowa z wykorzystaniem
falek Haara
Alfréd Haar
1885 -1933
2
Przypomnijmy, że istotą DWT jest podział
pierwotnego sygnału za pomocą pary filtrów
(górnoprzepustowego i dolnoprzepustowego) na
dwie składowe i następnie hierarchiczna
dekompozycja jednej z tych składowych
(niskoczęstotliwościowej) w analogiczny sposób.
3
Pojedynczy krok wielopoziomowej
dekompozycja danych
1000 próbek
dolnoprzepustowy
Filtry
~1000 próbek
górnoprzepustowy
~1000 próbek
2
2
cA
~500
współczynników
~500
współczynników
cD
4
Na każdym etapie realizacji piramidy Mallata
wykonywana jest bazowa operacja splotu wejściowego szeregu
danych x(n) z dwoma zestawami współczynników wagowych:
współczynniki odpowiedzi impulsowej filtru
dolnoprzepustowego
Współczynniki
aproksymacji
a
(i)
n
L − 1
= ∑ g m ⋅ a 2( in−+1 m) ,
m =0
i = 1, K ,
współczynniki odpowiedzi impulsowej filtru
górnoprzepustowego
detale
d
(i)
n
L − 1
= ∑ h m ⋅ a 2( in−+1m) ,
m =0
a n( 0 ) = x ( n )
oraz operacja „downsamplingu” – odrzucania co drugiej próbki
odfiltrowanego sygnału w każdej ze składowych w celu redukcji
5
nadmiarowości zbioru danych.
Na
dzień
dzisiejszy
istnieje
wiele
opracowanych zestawów współczynników filtrów.
Są to filtry Haara, Daubechies, Coiflety, Simflety
i inne.
6
DWT w bazie Haara jest najprostszym,
lecz dość skutecznym sposobem wieloskalowej
reprezentacji danych.
Zastosowanie
Zastosowanie filtrów
filtrów Haara
Haara powoduje,
powoduje, że
że na
na
każdym
etapie
dekompozycji
procedura
każdym
etapie
dekompozycji
procedura
dolnoprzepustowej
dolnoprzepustowej filtracji
filtracji sprowadza
sprowadza się
się do
do
obliczania
obliczania znormalizowanej
znormalizowanej wartości
wartości średniej
średniej
sąsiednich
sąsiednich elementów
elementów sekwencji
sekwencji danych,
danych, zaś
zaś
procedura
procedura filtracji
filtracji górnoprzepustowej
górnoprzepustowej –– do
do
obliczania
obliczania znormalizowanej
znormalizowanej różnicy
różnicy tych
tych
samych
samych elementów.
elementów.
7
Filtr pasmowy H przekształca wejście x w
wyjście y=H(x).
Jeśli filtr pasmowy jest liniowy, to
odpowiednie
transformaty
mogą
być
reprezentowane jako macierz H, a obliczenie
transformaty sygnału X osiąga się przez obliczenie
mnożenia macierzy Y=H·X.
8
Poniższy schemat pokazuje dobrze znany
przykład filtru pasmowego stosowanego do
analizy, który rozdziela częstotliwości sygnału
dyskretnego na niskie i wysokie.
H0
H0
(n )
⋅X
↓? 2
Y0 = D ( n ) H 0
(n )
⋅X
⎡Y ⎤
Y = ⎢ 0⎥
⎣Y1 ⎦
x
H1
H1
(n )
⋅X
↓? 2
Y1 = D ( n ) H 1
(n )
⋅X
9
Jako przykład obliczmy macierz H dla filtru
pasmowego Haara, biorąc wejście X zawierające N
próbek.
Operacja
ta
dla
filtru
niskoczęstotliwościowego może być przedstawiona za
pomocą macierzy:
H0
(n )
⎡1 1
⎤
⎢ 1 1
⎥
⎢
⎥
⎥
1 1
1 ⎢
=
⎢
⎥
O
2⎢
⎥
⎢
1 1⎥
⎢
⎥
1⎥⎦
⎢⎣
Należy przypomnieć, że filtr
dolnoprzepustowy Haara H0
uśrednia sąsiednie elementy
wejścia.
10
Filtr górnoprzepustowy Haara H1 oblicza
połowę różnicy pomiędzy kolejnymi próbkami
wejściowymi, co może być przedstawione za
pomocą macierzy:
H1
(n )
⎤
⎡1 − 1
⎥
⎢
1 −1
⎥
⎢
⎥
1 −1
1 ⎢
=
⎥
⎢
O
2⎢
⎥
⎢
1 − 1⎥
⎥
⎢
1 ⎥⎦
⎢⎣
11
Operacja
downsamplingu
może
reprezentowana za pomocą macierzy:
D (n )
⎡1
⎢0
⎢
= ⎢0
⎢
⎢M
⎢⎣0
być
0 0 0 0 ... 0 0⎤
⎥
0 1 0 0 ... 0 0⎥
0 0 0 1 ... 0 0⎥
⎥
⎥
0 0 0 0 ... 1 0⎥⎦
która wybiera pierwszy, trzeci, itd. element X.
12
Połączona
operacja
filtrowania
dolnoprzepustowego i downsamplingu może być
reprezentowana za pomocą macierzy:
(n )
L
(n )
= D H0
(n )
⎤
⎡1 1
⎥
⎢
1 1
⎥
⎢
1
⎥
⎢
=
...
2⎢
⎥
1 1
⎥
⎢
⎢⎣
1 1⎥⎦
13
Podobnie, połączona operacja filtracji
wysokoprzepustowej i downsamplingu jest
reprezentowana jako:
B
(n )
(n )
= D H1
(n )
⎡1 − 1
⎤
⎢
⎥
−
1
1
⎥
1 ⎢
⎢
⎥
=
...
2⎢
⎥
1 −1
⎢
⎥
⎢⎣
1 − 1⎥⎦
14
Górna i dolna gałąź filtru pasmowego
wytwarza odpowiednio:
(n )
Y0 = L X
Y1 = B (n ) X
Wyjściem filtru pasmowego jest:
(n )
⎡
Y
L
⋅ X⎤
⎡ 0⎤
⎢
⎥
⎢
⎥
Y = ⎢ − ⎥ = ⎢ − ⎥ = H (n ) ⋅ X ∈, gdzie
⎢⎣ Y1 ⎥⎦ ⎢⎣B ( n ) ⋅ X⎥⎦
H (n)
⎡ L(n ) ⎤
⎢
⎥
= ⎢ − ⎥∈
⎢B ( n ) ⎥
⎣
⎦
15
Możemy także zbudować hierarchiczną
reprezentację sygnału poprzez rekursywne
filtrowanie niskoprzepustowego wyjścia filtru
pasmowego:
16
W każdym kroku rekursji wielkość sygnału
zmniejsza się dwukrotnie.
Jeśli sygnał jest dyskretny i skończony (i jego
długość jest potęgą dwójki), to możemy w
ostateczności uzyskać sygnał o długości jednej
próbki.
Suma wymiarów wszystkich wyjść jest równa
wymiarowi oryginalnego sygnału wejściowego.
17
Ostateczna,
hierarchiczna
reprezentacja
sygnału wejściowego jest zbiorem współczynników
szczegółowości o różnych poziomach rozkładu
(skale) i gruboziarnistą wersją oryginalnego
sygnału (wyjście filtru dolnoprzepustowego).
18
Operację analizy falkowej w całym bloku
filtrującym można przedstawić w postaci
macierzowej za pomocą następującego równania
macierzowego:
⎡ a0 ⎤
⎤ ⎡ x0 ⎤
⎡1 1
⎢ c ⎥
⎥ ⎢ x ⎥
⎢1 − 1
⎢ 0 ⎥
⎥ ⎢ 1 ⎥
⎢
⎢ a1 ⎥
⎥ ⎢ x2 ⎥
⎢
1 1
1 ⎢
⎥
⎢
⎥
⎥ ⎢
•
=
c
x
1 −1
⎢ 1 ⎥
⎥ ⎢ 3 ⎥
⎢
2⎢
⎢ M ⎥
⎥ ⎢ M ⎥
O
⎥
⎢
⎥
⎥ ⎢
⎢
1 1 ⎥ ⎢ x N −2 ⎥
⎢a N −1 ⎥
⎢
⎢c ⎥
⎥ ⎢x ⎥
⎢
1
1
−
⎦ ⎣ N −1 ⎦
⎣
⎣ N −1 ⎦
19
Odwrotną
transformatę
Haara
przedstawić w następujący sposób:
można
20
Wzór na odtworzenie współczynnika
aproksymacji będzie miał postać:
a1(n-1) = (L(n))T·a2(n) + (B(n))T·c2(n),
gdzie macierze (L(n))T i (B(n))T wyglądają
następująco:
21
⎡1
⎤
⎢1
⎥
⎢
⎥
⎢ 1
⎥
⎢
⎥
1
⎢
⎥
1
⎥
=⎢
(L(n ) ) Τ =
M
⎥
2 ⎢
1 ⎥
⎢
⎢
1 ⎥
⎢
⎥
1⎥
⎢
⎢
⎥
1
⎣
⎦
22
⎡1
⎢− 1
⎢
⎢
1
⎢
−1
⎢
1
(n ) Τ
(B ) =
=⎢
M
2 ⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
−1
⎥
⎥
1
⎥
1⎥
− 1⎥⎦
23
Operacja rekonstrukcji sygnału w całym
bloku filtrującym będzie miała postać:
⎡ x0 ⎤
⎡1 1
⎤ ⎡ a0 ⎤
⎢ x ⎥
⎢1 − 1
⎥ ⎢ c ⎥
⎢ 1 ⎥
⎢
⎥ ⎢ 0 ⎥
⎢ x2 ⎥
⎢
⎥ ⎢ a1 ⎥
1 1
1 ⎢
⎢
⎥
⎥
⎥ ⎢
1 −1
⎢ x3 ⎥ =
⎢
⎥ • ⎢ c1 ⎥
2⎢
⎢ M ⎥
⎥ ⎢ M ⎥
O
⎢
⎥
⎥
⎢
⎥ ⎢
1 1 ⎥ ⎢a N −1 ⎥
⎢ x N −2 ⎥
⎢
⎢x ⎥
⎢
⎥ ⎢c ⎥
−
1
1
⎣
⎦ ⎣ N −1 ⎦
⎣ N −1 ⎦
24
Przykłady:
Transformata Falkowa Haara dla N=8
X = [x 0
H0
x∈R
(1)
(1)
a
0
?↓22
n
x1
x2
H 0(2)
H 1(2)
H1
(1)
x3
x4
?↓22 a1
?↓22 c1
x5
(2)
(2)
x6
H0
x7 ]
Τ
(3)
H 1(3)
(3)
a
2
?↓22
?↓22
c2(3)
(1)
c
0
?↓22
25
Krok 1:
a0(1) = D(1)H0(1) · X = L(1) · X ,
c0(1) = D(1)H1(1) · X= =B(1) · X
Macierze
dla
wyglądają następująco:
H0
(1)
⎛1
⎜
⎜0
⎜0
⎜
1 ⎜0
=
⎜
2 ⎜0
⎜0
⎜
⎜0
⎜0
⎝
odpowiednich
filtrów
1 0 0 0 0 0 0⎞
⎛1 −1 0 0 0 0 0 0 ⎞
⎟
⎜
⎟
1 1 0 0 0 0 0⎟
⎜0 1 −1 0 0 0 0 0 ⎟
⎜0 0 1 −1 0 0 0 0 ⎟
0 1 1 0 0 0 0⎟
⎟
⎜
⎟
0 0 1 1 0 0 0 ⎟ (1)
1 ⎜0 0 0 1 −1 0 0 0 ⎟
=
H
⎜
⎟
0 0 0 1 1 0 0 ⎟⎟ 1
2 ⎜0 0 0 0 1 −1 0 0 ⎟
⎜0 0 0 0 0 1 −1 0 ⎟
0 0 0 0 1 1 0⎟
⎟
⎜
⎟
0 0 0 0 0 1 1⎟
0
0
0
0
0
0
1
1
−
⎜
⎟
⎜ 0 0 0 0 0 0 26
0 0 0 0 0 0 1 ⎟⎠
0 1 ⎟⎠
⎝
Operacja
downsamplingu
reprezentowana przez macierz:
D (1)
⎛1
⎜
⎜0
=⎜
0
⎜
⎜0
⎝
będzie
0 0 0 0 0 0 0⎞
⎟
0 1 0 0 0 0 0⎟
0 0 0 1 0 0 0⎟
⎟
0 0 0 0 0 1 0 ⎟⎠
Macierze przekształceń L i B mają więc
postać:
⎛1
⎜
1 ⎜0
L(1) =
2 ⎜⎜ 0
⎜0
⎝
1 0 0 0 0 0 0⎞
⎛1 −1
⎟
⎜
0 1 1 0 0 0 0⎟
1 ⎜0 0
(1)
B
=
⎜0 0
0 0 0 1 1 0 0⎟
2
⎜
⎟
⎜0 0
⎟
0 0 0 0 0 1 1⎠
⎝
0⎞
⎟
0⎟
1 −1 0 0 ⎟
⎟
0 0 1 − 1⎟⎠
0 0 0
1 −1 0
0
0
0
0
0
0
0
0
27
W wyniku otrzymujemy wektory:
a0
c0
(1)
(1)
⎡ x0 + x1
=⎢
2
⎣
⎡ x 0 − x1
=⎢
2
⎣
x 2 + x3
2
x 2 − x3
2
x 4 + x5
2
x 4 − x5
2
x6 + x7 ⎤
⎥
2 ⎦
Τ
x6 − x7 ⎤
⎥
2 ⎦
Τ
28
Krok 2:
a1(2) = D(2)H0(2) · a0(1) = L(2)·a0(1),
c1(2) = D(2)H1(2) · a0(1) = B(2)· a0(1)
Macierze
dla
odpowiednich
wyglądają następująco:
H0
(2 )
⎛1
⎜
1 ⎜0
=
2 ⎜⎜ 0
⎜0
⎝
filtrów
1 0 0⎞
⎛1 −1 0 0 ⎞
⎟
⎟
⎜
1 1 0⎟
1 ⎜0 1 −1 0 ⎟
(2 )
H1 =
⎟
⎜ 0 0 1 − 1⎟
0 1 1
2
⎟
⎟
⎜
⎟
⎟
⎜0 0
0 0 1⎠
0
1
⎠
⎝
29
Operacja
downsamplingu
reprezentowana przez macierz:
D
(2 )
będzie
⎛1 0 0 0⎞
⎟⎟
= ⎜⎜
⎝0 0 1 0⎠
Macierze przekształceń L i B mają więc
postać:
1 ⎛1 1 0 0⎞
⎜⎜
⎟⎟
L =
2 ⎝0 0 1 1⎠
(1)
B
(1)
1 ⎛1 −1 0 0 ⎞
⎜⎜
⎟⎟
=
2 ⎝ 0 0 1 − 1⎠
30
W wyniku otrzymamy wektory:
a1
c1
( 2)
( 2)
⎡ x0 + x1 + x 2 + x3
=⎢
2
⎣
x 4 + x5 + x 6 + x 7 ⎤
⎥
2
⎦
⎡ x 0 + x1 − x 2 − x3
=⎢
2
⎣
x 4 + x5 − x6 − x7 ⎤
⎥
2
⎦
T
T
31
Krok 3:
a2(3) = D(3)H0(3) · a1(2) = L(3) · a1(2),
c2(3) = D(3)H1(3) · a1(2) = B(3)· a1(2)
H0
(3 )
1 ⎛ 1 1⎞
⎜⎜
⎟⎟
=
2 ⎝ 0 1⎠
H1
(3 )
1 ⎛ 1 − 1⎞
⎜⎜
⎟⎟
=
2 ⎝0 1 ⎠
Operacja downsamplingu będzie reprezentowana
przez macierz:
D (3 ) = (1 0 )
32
Macierze przekształceń L i B mają więc
postać:
(3 )
L
=
1
2
(1 1)
B
(3 )
=
1
2
(1
− 1)
Otrzymamy skalary:
a2
c2
( 3)
( 3)
=
=
x0 + x1 + x 2 + x3 + x 4 + x5 + x6 + x7
2 2
x 0 + x1 + x 2 + x3 − x 4 − x5 − x6 − x7
2 2
33
Odwrotna Transformata Falkowa Haara N=8
Krok 1:
a1(2) = (L(3))T·a2(3) + (B(3))T·c2(3)
1 ⎛1⎞
⎜⎜ ⎟⎟
(L ) =
2 ⎝1⎠
(3 )
a1
( 2)
Τ
B
(3 )
1 ⎛1⎞
⎜⎜ ⎟⎟
=
2 ⎝ − 1⎠
⎡ x0 + x1 + x 2 + x3 + x 4 + x5 + x 6 + x7 ⎤ ⎡ x0 + x1 + x 2 + x3 − x 4 − x5 − x6 − x7 ⎤
⎥
⎥ ⎢
⎢
2
2
2
2
=⎢
⎥=
⎥+⎢
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
−
−
−
−
+
+
+
+
+
+
+
+
+
+
+
1
2
3
4
5
6
7 ⎥
1
2
3
4
5
6
7 ⎥
⎢ 0
⎢ 0
⎥⎦
⎥⎦ ⎢⎣
⎢⎣
2 2
2 2
⎡ x0 + x1 + x 2 + x3 ⎤
⎥
⎢
2
⎢x + x + x + x ⎥
5
6
7
⎥
⎢ 4
2
⎦
⎣
34
Krok 2:
a0(1) = (L(2))T·a1(2) + (B(2))T·c1(2)
⎛1
⎜
1 ⎜1
(2 ) Τ
(L ) =
2 ⎜⎜ 0
⎜0
⎝
a0
(1)
0⎞
⎟
0⎟
1⎟
⎟
1 ⎟⎠
⎡ x0 + x1 + x 2
⎢
2 2
⎢
⎢ x0 + x1 + x 2
⎢
2 2
=⎢
x 4 + x5 + x6
⎢
2 2
⎢
⎢ x 4 + x5 + x6
⎢
2 2
⎣
0⎞
⎛1
⎟
⎜
1 ⎜−1 0 ⎟
(1) Τ
(B ) =
2 ⎜⎜ 0 1 ⎟⎟
⎜ 0 − 1⎟
⎠
⎝
+ x3 ⎤ ⎡ x 0 + x1 − x 2 − x3 ⎤ ⎡ x0 + x1 ⎤
⎥
⎥ ⎢
⎥ ⎢
2
2
2
⎥
⎥ ⎢
⎥ ⎢
+ x3 ⎥ ⎢ − x0 − x1 + x 2 + x3 ⎥ ⎢ x 2 + x3 ⎥
⎥
⎥ ⎢
⎥ ⎢
2
2
2
=
+
+ x 7 ⎥ ⎢ x 4 + x5 − x 6 − x 7 ⎥ ⎢ x 4 + x5 ⎥
⎥
⎥ ⎢
⎥ ⎢
2 2
2 ⎥
⎥ ⎢
⎥ ⎢
+ x 7 ⎥ ⎢ − x 4 − x5 + x6 + x 7 ⎥ ⎢ x6 + x7 ⎥
⎥ ⎢
⎥ ⎢
2 2
2 ⎥⎦
⎦ ⎣
⎦ ⎣
35
Krok 3: X = (L(1))T·a0(1) + (B(1))T·c0(1)
⎛1
⎜
⎜1
⎜0
⎜
1 ⎜0
(1) Τ
(L ) =
⎜0
2⎜
⎜0
⎜
⎜0
⎜0
⎝
0 0 0⎞
⎟
0 0 0⎟
1 0 0⎟
⎟
1 0 0⎟
0 1 0 ⎟⎟
0 1 0⎟
⎟
0 0 1⎟
0 0 1 ⎟⎠
0 0 0⎞
⎛1
⎜
⎟
⎜−1 0 0 0 ⎟
⎜0 1
0 0⎟
⎜
⎟
1 ⎜ 0 −1 0 0 ⎟
(1) Τ
(B ) =
⎜
0 ⎟⎟
2⎜ 0 0 1
⎜ 0 0 −1 0 ⎟
⎜
⎟
0
0
0
1
⎜
⎟
⎜ 0 0 0 − 1⎟
⎝
⎠
36
⎡ x0
⎢
⎢x
⎢ 0
⎢
⎢ x2
⎢
⎢x
⎢ 2
X=⎢
⎢ x4
⎢
⎢x
⎢ 4
⎢
⎢ x6
⎢
⎢x
⎢ 6
⎣
+ x1 ⎤ ⎡ x 0 − x1 ⎤
⎥
2 ⎥ ⎢
2
+ x1 ⎥ ⎢ − x 0 + x1 ⎥
⎥
⎥ ⎢
2 ⎥ ⎢
2
⎥ ⎡ x0 ⎤
+ x3 ⎥ ⎢ x 2 − x3 ⎥ ⎢ x ⎥
⎢ 1⎥
⎥
⎢
⎥
2
2
⎢ ⎥
⎢
⎥
+ x3
− x 2 + x3 ⎥ ⎢ x 2 ⎥
⎥
⎥ ⎢
2 ⎥+⎢
2
⎥ = ⎢ x3 ⎥
+ x5 ⎥ ⎢ x 4 − x5 ⎥ ⎢ x 4 ⎥
⎥ ⎢ ⎥
2 ⎥ ⎢
2
x5 ⎥
⎢
⎥
⎢
⎥
+ x5
− x + x5
⎥ ⎢ x6 ⎥
⎥ ⎢ 4
2 ⎥ ⎢
2
⎥ ⎢ ⎥
+ x 7 ⎥ ⎢ x 6 − x 7 ⎥ ⎢⎣ x 7 ⎥⎦
⎥
2 ⎥ ⎢
2
+ x7 ⎥ ⎢ − x6 + x7 ⎥
⎥
⎥ ⎢
2 ⎦ ⎣
2
⎦
37
Graf algorytmu transformaty falkowej
w baze Haara dla N=8
( x0 + x1 )
1 ⎛ 1
⎜
( x0 + x1 ) + 1 (x 2 + x 3 )⎞⎟
2⎝ 2
2
⎠
1 ⎛ 1 ⎛ 1
⎜⎜
⎜
(x 0 + x1 ) + 1 (x 2 + x3 )⎞⎟ + 1 ⎛⎜ 1 (x 4 + x5 ) + 1 (x 6 + x 7 )⎞⎟ ⎞⎟⎟
2⎝ 2⎝ 2
2
2⎝ 2
2
⎠
⎠⎠
(x 2 + x3 )
1 ⎛ 1
1
(x 4 + x5 ) + (x 6 + x7 )⎞⎟
⎜
2⎝ 2
2
⎠
1 ⎛ 1 ⎛ 1
1
1
1
1
⎞
⎜⎜
⎜
(x 0 + x1 ) + (x 2 + x3 )⎞⎟ − ⎛⎜ ( x4 + x5 ) + (x 6 + x 7 )⎞⎟ ⎟⎟
2 ⎝ 2⎝ 2
2
2⎝ 2
2
⎠
⎠⎠
(x 4 + x5 )
1 ⎛ 1
1
(x0 − x1 ) + (x2 − x3 )⎞⎟
⎜
2⎝ 2
2
⎠
1 ⎛ 1
1
⎜
(x 0 + x1 ) − ( x2 + x3 )⎞⎟
2⎝ 2
2
⎠
(x6 + x7 )
1 ⎛ 1
1
(x 4 − x5 ) + (x6 − x7 )⎞⎟
⎜
2⎝ 2
2
⎠
1 ⎛ 1
1
(x 4 − x5 ) + (x6 − x7 )⎞⎟
⎜
2⎝ 2
2
⎠
x0
1
x1
1
x2
1
x3
1
x4
1
x5
1
x6
1
x7
1
(x 6 − x7 )
2
2
2
2
2
2
2
2
(x0 − x1 )
1
(x 2 − x3 )
1
(x 4 − x5 )
1
2
2
2
(x0 − x1 )
(x 2 − x3 )
(x 4 − x5 )
1
(x 6 − x7 )
2
38
Dyskretna transformata
falkowa z wykorzystaniem
filtrów Daubechies
Ingrid Daubechies
39
Jest kilka rodzajów filtrów Daubechies:
DAUB2, DAUB4, ... , DAUB20.
Najprostszą jest falka DAUB4, która ma
cztery współczynniki: , gdzie:
c0 =
1+ 3
4 2
, c1 =
3+ 3
4 2
, c2 =
3− 3
4 2
, c3 =
1− 3
4 2
40
Macierz pojedynczej iteracji transformaty
Daubechies jest dana w postaci:
⎡c 0
⎢c
⎢ 3
⎢
⎢
⎢
⎢ ...
T=⎢
⎢ ...
⎢
⎢
⎢
⎢c
⎢ 2
⎢⎣ c1
c1
− c2
...
...
c2
c1
c3
− c0
c0
c3
c1
− c2
c2
c1
c3
− c0
...
...
c0
c1
c2
c3
− c2
c3
c1
c0
− c0
c3
gdzie puste pozycje oznaczając zera.
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
c3 ⎥
⎥
− c0 ⎥
c1 ⎥
⎥
− c 2 ⎥⎦
Wiersze
nieparzyste
reprezentują
filtrację
dolnoprzepustową, a wiersze parzyste operację filtracji
41
górnoprzepustowej
Procedura polega na przemnożeniu wektora
danych
wejściowych
X
przez
macierz
transformaty T.
Oryginalny wektor X ma długość N, gdzie N
musi być potęgą dwójki.
Konsekwentnie macierz filtrowania w
pierwszym kroku rekursji ma rozmiar N×N.
W następnym kroku rekursji macierz ma
rozmiar ½N×½N
42
Operacja odwrotna polega na przemnożeniu
wektora
współczynników
przez
macierz
odwrotną, która jest po prostu transpozycją
macierzy transformaty.
T −1
⎡c 0
⎢c
⎢ 1
⎢c 2
⎢
⎢ c3
= TΤ = ⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
c3
− c2
c1
− c0
c2
c3
c0
c1
c3
− c2
O
c2
c3
c1
− c0
c0
c1
c2
c3
c3
− c2
c1
− c0
c0
c1
c1 ⎤
− c0 ⎥⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
c3 ⎥
− c 2 ⎥⎦
43
Macierz TT jest odwrotną do macierzy T,
wtedy i tylko wtedy, gdy zachodzą dwa równania:
2
2
2
2
c0 + c1 + c 2 + c3 = 1
c 2 c0 + c3 c1 = 0
Dodatkowo potrzebujemy zależności:
c3 − c 2 + c1 − c 0 = 0
0 ⋅ c3 − 1 ⋅ c 2 + 2 ⋅ c1 − 3 ⋅ c0 = 0
44
c0 + c1 + c 2 + c3 = 1 c3 − c 2 + c1 − c 0 = 0
2
2
2
2
c 2 c0 + c3 c1 = 0
0 ⋅ c3 − 1 ⋅ c 2 + 2 ⋅ c1 − 3 ⋅ c0 = 0
Równania te są czterema równaniami z
czterema niewiadomymi c0, c1, c2, c3 po raz pierwszy
odkrytymi przez Ingrid Daubechies.
Rozwiązaniem tych równań są
współczynniki przedstawione już wcześniej:
c0 =
1+ 3
4 2
, c1 =
3+ 3
4 2
, c2 =
3− 3
4 2
, c3 =
cztery
1− 3
4 2
45
DAUB4 jest najbardziej zwartym zbiorem ze
zbiorów współczynników falkowych.
Jeśli będziemy mieli sześć współczynników
w miejsce czterech, otrzymamy rozwiązanie
postaci.
c0 =
c3 =
1 + 10 + 5 + 2 10
16 2
, c1 =
10 − 2 10 − 2 5 + 2 10
16 2
5 + 10 + 3 5 + 2 10
, c4 =
16 2
, c2 =
5 + 10 − 3 5 + 2 10
16 2
10 − 2 10 + 2 5 + 2 10
, c5 =
16 2
1 + 10 − 5 + 2 10
16 2
To jest zbior wspólczynnikoów DAUB6.
46
,
Przykład:
Transformata Falkowa „Daubechies-4”, N=8
X = [x 0
Krok 1:
x1
x2
x3
a0(1) = L(1)·X
x4
x5
x6
x7 ]
Τ
c0(1) = B(1)·X
47
Macierze
dla
odpowiednich
wyglądają następująco:
⎡c 0
⎢
L(1) = ⎢
⎢
⎢
⎣c 2
B
(1)
⎡c 3
⎢
=⎢
⎢
⎢
⎣ c1
c1
c2
c3
c0
c1
c2
c0
c3
c1
c3
− c2
− c0
c2
c0
c1
c3
− c0
− c2
c1
c3
− c0
− c2
c1
c3
filtrów
⎤
⎥
⎥
c3 ⎥
⎥
c1 ⎦
⎤
⎥
⎥
− c0 ⎥
⎥
− c2 ⎦
48
W wyniku otrzymamy dwa wektory o
wymiarze 4×1: a0(1) i c0(1).
Krok 2:
a1(2) = L(2)·a0(1)
c1(2) = B(2)·a0(1)
Macierze dla odpowiednich filtrów mają
postać:
(2 )
L
⎡c 0
=⎢
⎣c 2
c1
c3
c2
c0
c3 ⎤
⎥
c1 ⎦
B
(2 )
⎡c 3
=⎢
⎣ c1
− c2
− c0
c1
c3
− c0 ⎤
− c 2 ⎥⎦
W wyniku otrzymamy dwa wektory o
wymiarze 2×1: a1(2) i c1(2).
49
W ten sposób otrzymaliśmy zakończyliśmy
proces transformaty, którą można przedstawić za
pomocą schematu:
⎡a1 (2 ) 0 ⎤
⎡a 0 (1) 0 ⎤
⎡ x0 ⎤
⎢ (2 ) ⎥
⎢ (1) ⎥
⎢x ⎥
⎢ a1 1 ⎥
⎢ a0 1 ⎥
⎢ 1⎥
⎢ c (2 ) 0 ⎥
⎢a (1) 2 ⎥
⎢ x2 ⎥
⎢ 1 (2 ) ⎥
⎢ 0 (1) ⎥
⎢ ⎥
⎢ x 3 ⎥ → ⎢ a 0 3 ⎥ → ⎢ c1 1 ⎥
⎢ c (1) 0 ⎥
⎢ c (1) 0 ⎥
⎢ x4 ⎥
⎢ 0 (1) ⎥
⎢ 0 (1) ⎥
⎢ ⎥
⎢ c0 1 ⎥
⎢ c0 1 ⎥
⎢ x5 ⎥
⎢ c (1) ⎥
⎢ c (1) ⎥
⎢x ⎥
⎢ 0 2⎥
⎢ 0 2⎥
⎢ 6⎥
⎢⎣ c0 (1) 3 ⎥⎦
⎢⎣ c0 (1) 3 ⎥⎦
⎢⎣ x7 ⎥⎦
50
Odwrotna transformata falkowa
„Daubechies-4”, N=8
Krok 1:
a0(1) = (L(2))T ·a1(2) + (B(2))T ·c1(2)
Macierze dla odpowiednich filtrów wyglądają
następująco:
⎡c 0
⎢c
1
(2 ) Τ
⎢
(L ) =
⎢c 2
⎢
⎣ c3
c2 ⎤
⎥
c3 ⎥
c0 ⎥
⎥
c1 ⎦
⎡ c3
⎢− c
(B ( 2 ) ) Τ = ⎢ 2
⎢ c1
⎢
⎣− c0
c1 ⎤
− c0 ⎥⎥
c3 ⎥
⎥
− c2 ⎦
51
Krok 2:
X = (L(1))T·a0(1) + (B(1))T·c0(1)
Macierze dla odpowiednich filtrów mają
postać:
⎡c 0
⎢c
⎢ 1
⎢c 2
⎢
c3
(1) Τ
⎢
(L ) =
⎢
⎢
⎢
⎢
⎢
⎢⎣
c0
c1
c2
c3
c0
c1
c2
c3
c2 ⎤
c3 ⎥⎥
⎥
⎥
⎥
⎥
⎥
⎥
c0 ⎥
⎥
c1 ⎥⎦
⎡ c3
⎢− c
⎢ 2
⎢ c1
⎢
− c0
(1) Τ
⎢
(B ) =
⎢
⎢
⎢
⎢
⎢
⎢⎣
c3
− c2
c1
− c0
c3
− c2
c1
− c0
c1 ⎤
− c0 ⎥⎥
⎥
⎥
⎥
⎥
⎥
⎥
c3 ⎥
⎥
− c 2 ⎥⎦
W ten sposób odzyskujemy wektor X o
52
wymiarze 1 × 8.
Jeśli chcemy podobnie jak w transformacie
Haara w ostatnim kroku uzyskać skalary, musimy
zastosować transformatę, w której współczynniki
aproksymacji i szczegółowości obliczamy z
następujących równań:
ai = c0 ⋅ x 2i + c1 ⋅ x 2i +1 + c 2 ⋅ x 2i + 2 + c3 ⋅ x 2i +3
ci = c3 ⋅ x 2i − c 2 ⋅ x 2i +1 + c1 ⋅ x 2i + 2 − c0 ⋅ x 2i +3
Macierze odpowiednich filtracji będą
miały postać:
53
⎡c 0
⎢0
L(1) = ⎢
⎢0
⎢
⎣0
B (1)
⎡c 3
⎢0
=⎢
⎢0
⎢
⎣0
c1
c2
c3
0
0
0
0
0
0
c0
0
c1
0
c2
c0
c3
c1
0
c2
0
c3
0
0
0
0
0
c0
c1
− c2
0
0
c1
c3
0
− c0
− c2
0
0
c1
c3
0
− c0
− c2
0
0
c1
0
0
− c0
0
0
0
0
0
c3
− c2
c2
⎤
⎥
⎥
⎥
⎥
c3 ⎦
c1
⎤
⎥
⎥
⎥
⎥
− c0 ⎦
54
W ostatniej iteracji współczynniki macierzy
będą mnożone przez elementy sygnału: xN-2, xN-1,
xN i xN+1.
⎡c 0
⎢0
L(1) = ⎢
⎢0
⎢
⎣0
B (1)
⎡c 3
⎢0
=⎢
⎢0
⎢
⎣0
c2
c0
0
0
c3
c1
0
0
0
c2
c0
0
0
c3
c1
0
0
0
c2
c0
0
0
c3
c1
− c2
0
0
c1
c3
0
− c0
− c2
0
0
c1
c3
0
− c0
− c2
0
0
c1
0
0
− c0
0
0
0
0
0
c3
− c2
c1
0
0
0
c2
⎤
⎥
⎥
⎥
⎥
c3 ⎦
c1
⎤
⎥
⎥
⎥
⎥
− c0 ⎦
I tu pojawi się
problem, ponieważ
xN i xN+1 nie
istnieją.
55
Istnieją trzy metody radzenia sobie z tym
problemem:
1. Potraktowanie
okresowych.
zbioru
danych
jako
Na początek sekwencji danych wstawiamy
końcowe elementy sygnału (w przypadku DWT),
lub na końcu wektora umieszczamy początkowe
elementy sekwencji danych (w przypadku
IDWT).
56
2. Powturzenie
skrajnich
elementów
znajdujących się po każdej stronie wektora
danych (na początku i na końcu) tyle razy ile
jest to konecznie dla uzupelnienia nezbędnej
dlugości wektora.
3. Dopisywanie po jednej lub obydwu stronach
wektora danych odpowiedniej licby „zer”.
57
Krok 1: W pierwszym kroku będziemy więc
mnożyć macierz L(1) i macierz B(1) przez wektor:
X = [x6
x7
x0
x1
x2
x3
x4
x5
x6
x7 ]
Τ
Otrzymamy:
a0
(1)
⎡ c3 x6 − c 2 x7 + c1 x0 − c 0 x1 ⎤
⎡ c0 x6 + c1 x7 + c 2 x0 + c3 x1 ⎤
⎢c x − c x + c x − c x ⎥
⎢c x + c x + c x + c x ⎥
(1)
3 0
2 1
1 2
0 3⎥
0 0
1 1
2 2
3 3⎥
⎢
⎢
c
=
=
⎢c3 x 2 − c 2 x3 + c1 x 4 − c0 x5 ⎥
⎢c0 x 2 + c1 x3 + c 2 x 4 + c3 x5 ⎥ 0
⎢
⎥
⎢
⎥
⎣c0 x 4 + c1 x5 + c 2 x 6 + c3 x7 ⎦
⎣c3 x 4 − c 2 x5 + c1 x 6 − c0 x7 ⎦
58
Krok 2: W drugim kroku będziemy obliczać
równania: a1(2)=L(2)·a0(1)+ ; c1(2) = B(2)·a0(1)+,
gdzie wektor a0(1)+ jest wektorem a0(1), do którego
początku dodano dwa końcowe elementy, macierze
L(2) i B(2) będą miały postać
(2 )
L
B
(2 )
⎡c 0
=⎢
⎣0
⎡c 3
=⎢
⎣0
c1
0
c2
c0
c3
c1
− c2
0
c1
c3
− c0
− c2
c2
c1
⎤
c3 ⎥⎦
⎤
− c0 ⎥⎦
59
Krok 3: będziemy obliczać równania:
a2(3) = L(3) ·a1(2)+;
c2(3) = B(3) ·a1(2)+
L(3) = [c 0
c1
c2
c3 ]
B (3) = [c3
− c2
c1
− c0 ]
60
Operacja
odwrotna
następujących kroków:
składa
się
z
Krok 1: a1(2) = (L(3))T· a2(3)+ + (B(3))T· c2(3)+
gdzie macierze (L(3))T i (B(3))T mają postać:
⎡c 0 ⎤
⎢c ⎥
(L(3 ) ) Τ = ⎢ 1 ⎥
⎢c 2 ⎥
⎢ ⎥
⎣ c3 ⎦
⎡ c3 ⎤
⎢− c ⎥
( B (3 ) ) Τ = ⎢ 2 ⎥
⎢ c1 ⎥
⎥
⎢
⎣− c0 ⎦
61
Krok 2: a0(1) = (L(2))T· a1(2)+ + (B(2))T· c1(2)+,
gdzie macierze (L(2))T i (B(2))T mają postać:
⎡c 0
⎢c
⎢ 1
⎢c 2
(2 ) Τ
(L ) = ⎢
⎢ c3
⎢
⎢
⎢⎣
0⎤
0 ⎥⎥
c0 ⎥
⎥
c1 ⎥
c2 ⎥
⎥
c3 ⎥⎦
⎡ c3
⎢− c
⎢ 2
⎢ c1
(2 ) Τ
(B ) = ⎢
⎢− c0
⎢
⎢
⎢⎣
0 ⎤
0 ⎥⎥
c3 ⎥
⎥
− c2 ⎥
c1 ⎥
⎥
− c0 ⎥⎦
62
Krok 3: X = a0(1)·(L(1))T + c0(1)·(B(1))T
⎡c 0
⎢c
⎢ 1
⎢c 2
⎢
⎢c3
⎢0
(1) Τ
(L ) = ⎢
⎢0
⎢0
⎢
⎢0
⎢
⎢
⎢⎣
0
0
0
c1
c2
0
0
c3
c4
0
0
0
c0
c1
c2
c3
0⎤
⎡ c3
⎢− c
0 ⎥⎥
⎢ 2
⎢ c1
0⎥
⎥
⎢
0⎥
⎢− c0
⎢ 0
0⎥
(1) Τ
⎥ (B ) = ⎢
0⎥
⎢ 0
⎢ 0
c0 ⎥
⎥
⎢
c1 ⎥
⎢ 0
⎢
c2 ⎥
⎥
⎢
c3 ⎥⎦
⎢⎣
0
0
c3
− c2
c1
− c0
0
0
0
0
0
0
c3
− c2
c1
− c0
0 ⎤
0 ⎥⎥
0 ⎥
⎥
0 ⎥
0 ⎥
⎥
0 ⎥
c3 ⎥
⎥
− c2 ⎥
c1 ⎥
⎥
− c0 ⎥⎦
63
64