Wykład 6 i 7

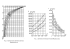
Naprężenia w ośrodku gruntowym
•
•
•
•
Naprężenia geostatyczne (pierwotne)
Wpływ wody gruntowej na naprężenia pierwotne
Naprężenia wywołane siłą skupioną
Naprężenia pochodzące od obciążenia równomiernie
rozłożonego
• Naprężenia pod fundamentem bezpośrednim
• Osiadania fundamentu bezpośredniego
Naprężenia wywołane ciężarem własnym gruntu (n. geostatyczne)
h
σ hγ =h ⋅γ
jednorodne podłoże gruntowe
o ciężarze objętościowym γ
wzór ogólny w przypadku podłoża
uwarstwionego:
n
σ hγ = ∑ mi ⋅γ i
i =1
1
Wpływ wody gruntowej na naprężenia pierwotne
h
σ hγ
γ
jednorodne podłoże gruntowe
hw
zw.w.g.
σ hγ = hw ⋅γ + ( h − hw )⋅γ '
γ
’
Naprężenia wywołane ciężarem własnym gruntu (n. geostatyczne)
Podziałka głębokości:
D
Podziałka naprężeń:
γ1
1m
20 kPa
h
z=0
γ1
z
m1
σ Dγ = D⋅ γ1
zwg
γ2
'
γ3
'
γ4
'
m2
z=0
z=0
m3
σ hr = D ⋅ γ1 + m1 ⋅γ 1 + (z − m1 )⋅ γ2'
m4
2
Osiadanie terenu wywołane obniżeniem poziomu wód podziemnych
Związek pomiędzy osiadaniem terenu a poziomem wody gruntowej na terenie Santa Clara
Valley, Kalifornia.
Źródło: Environmental Geology. Bennett M. R., Doyle P, John Willey & Sons, 1997
Osiadanie terenu w latach 1934–1960 na terenie Santa Clara Valley, Kalifornia.
Źródło: Groundwater. Freeze A. R., Cherry A. J. Prentice Hall, 1979
Naprężenia pionowe w półprzestrzeni gruntowej obciążonej siłą
skupioną - rozwiązanie Boussinesq’a (1885)
Założenia:
1.
Ośrodek gruntowy jest jednorodny i izotropowy (tzn. działanie jednakowych naprężeń w
dowolnym kierunku powoduje jednakowe odkształcenia
2.
Grunt jest materiałem sprężystym, tzn. podlega prawu Hooke’a
3.
Naprężenia rozchodzą się promieniście od punktu przyłożenia siły
4.
Nie uwzględnia się ciężaru własnego gruntu
5.
Obowiązuje zasada superpozycji
6.
Pionowo działające siła powoduje obniżenie się półkuli o dowolnym promieniu ze środkiem w
punkcie zaczepienia siły o jednakową wartość „S” Q
z
3
Naprężenia radialne w półprzestrzeni gruntowej obciążonej siłą skupioną
- rozwiązanie Boussinesq’a (1885)
R=σRA
Q
A
= cosα
A'
A
r
A’
α
R
R
z
σr
α
σz
M
σr =
3Q
cos α
2πR 2
Z=Rcosα
A’
σz =
Z R cosα R cos 2 α
=
=
= σ r cos 2 α
A
A'
A
cosα
Naprężenia pionowe w półprzestrzeni gruntowej obciążonej siłą
skupioną - rozwiązanie Boussinesq’a (1885)
Schemat obciążenia podłoża
Wzory
σz =
3Q
cos 3 α
2πR 2
σz =
3Q
cos 5 α
2πz 2
σz =
3Qz 3
2πR 5
σz =
3Qz 3
2π ( z 2 + r 2 ) 5 / 2
Q
r
α
R
z
σz
M
Podstawowe zależności:
cos α =
z
R
R = z2 + r2
σz =
3Q
  r 2 
2πz 2 1 +   
  z  
5/2
4
Graficzna ilustracja naprężeń
Izobary naprężeń radialnych i naprężeń pionowych
Q
-0.50
-1.00
-1.50
-2.00
-2.50
Naprężenia pionowe
-3.00
-2.00
Naprężenia radialne
-1.50
-1.00
-0.50
0.00
0.50
1.00
1.50
2.00
Graficzna ilustracja naprężeń
Izobary naprężeń pionowych – konstrukcja graficzna
Q
-
500
1000
2000
-0.50
2000
-1.00
1500
1000
-1.50
-2.00
500
-2.50
-3.00
-2.00
-1.50
-1.00
-0.50
0.00
0.50
1.00
1.50
2.00
5
Graficzna ilustracja naprężeń
Rozkład naprężeń na różnych głębokościach
Krzywa zanikania naprężeń
Q
σz
z1
z2
z3
z
Graficzna ilustracja naprężeń
Rozkład naprężeń wzdłuż prostej a, równoległej do kierunku działania siły Q
r
Q
a
σz
z1
z2
z3
z
6
Zasada superpozycji (Bolzmana) - sumowania naprężeń
Jeżeli siła Q1, powoduje w określonym miejscu ośrodka gruntowego naprężenie σ1, zaś siła
Q2 wywołuje w tym samym miejscu naprężenie σ2, to całkowite naprężenie w tym punkcie
ośrodka jest sumą naprężeń wywołanych przez każdą z sił z osobna.
Q1
Q2
r1 = 3.0 m
r 2 = 4.0 m
z = 3.0 m
M
Przykład obliczenia naprężenia:
σ zM = σ z (Q1 ) + σ z (Q2 ) =
σ zM =

3Q  
z
3Q
cos5 α1 + cos5 α 2 =
2πz 2   z 2 + r12
2πz 2

(
)
5
 
z
 +
  z2 + r2
2
 




5





5
5
3Q   3   3   Q
(0.177 + 0.078 ) = 0.0135Q [ kPa]

 +  =
2π 32   18   5   6π
Zamiana obciążenia równomiernie rozłożonego na zastępcze siły
skupione
q
Qi = q ⋅ ∆B ⋅ ∆L
ΔB
ΔL
L
Naprężenie pionowe wywołane
pojedynczą siłą zastępczą wynosi:
σ zi =
Qi
ri
3Qi
  r 2 
2πz 2 1 +  i  
  z  
5/2
R
i
B
z
Całkowite naprężenie pionowe stanowi sumę naprężeń od
wszystkich sił zastępczych (zasada superpozycji)
2
3Qi n   ri  
σ z = ∑ σ zi =
⋅
1
+




∑
2πz 2 i =1   z  
i =1
n
σzi
M
5/ 2
7
Wyznaczenie naprężenia pionowego σz od obciążenia ciągłego q za
pomocą elementarnych sił skupionych
q
y
B
dQ
dx
L
y
Naprężenie pionowe wywołane przez elementarną siłę
skupioną (q):
dy
dσ z =
r
x
x
M
R
3dQ
  r 2 
2πz 2 1 +   
  z  
5/ 2
=
3q
 x2 + y 2 
2πz 2 1 +
z 2 

5/ 2
Całkowite naprężenie pionowe stanowi sumę naprężeń od wszystkich elementarnych sił
zastępczych (zasada superpozycji):
dσ
z
z
L
σz = ∫
0
B
∫
0
3q
 x2 + y2 

2πz 2 1 +
z 2 

5/ 2
dxdy
Metoda punktów środkowych (Newmark i Polszin, 1935)
W przypadku gdy rozpatrywany punkt M znajduje się pod geometrycznym środkiem obciążającej
powierzchni prostokątnej naprężenie pionowe w tym punkcie oblicza się ze wzoru:
σ z = q ⋅η 0
gdzie:

L z
L

2 ⋅
2
B B
B
η0 = arctg
+
2
2
2
2
π
z
L
z
L
z
2
1 +   + 4 
1 +   + 4 

B
B
B
 
 
B
 B





1
1


+
⋅
2
2
2

 z 
 z  L
1 + 4    + 4  
 B 
B B








8
Nomogram do wyznaczania współczynnika η0
η
0,000
0,100
0,200
0,300
0,400
0
0,500
0,600
0,700
0,800
0,900
1,000
0,0
0,5
1,0
1,5
Z/B
2,0
L/B = 1
L/B = 1.5
2,5
L/B = 2
L/B = 3
3,0
L/B = 5
3,5
4,0
4,5
5,0
autor: Seweryn Szlachcic
Metoda punktów narożnych (Steinbrenner, 1936)
W przypadku gdy rozpatrywany punkt M znajduje się pod narożnikiem obciążającej powierzchni
prostokątnej naprężenie pionowe w tym punkcie oblicza się ze wzoru:
σ z = q ⋅η n
gdzie:

L
L z

⋅
1 
B
B B
+
ηn =
arctg
2
2
2
2
2π 
z
L  z 
L  z 
1+   +  
1+   +  

B
 B B
 B B





1
1
 
⋅
+
  z 2  L  2  z 2  
  +   
1 +  
 B   B  
 B
9
Nomogram do wyznaczania współczynnika ηn
ηn
0,000
0,050
0,100
0,150
0,200
0,250
0
1
2
3
4
L/B = 1
z/B
L/B = 1.5
5
L/B = 2
L/B = 3
6
L/B = 5
7
8
9
10
autor: Seweryn Szlachcic
Zastosowanie metody punktów narożnych do obliczania naprężeń
pionowych w dowolnym miejscu półprzestrzeni gruntowej (1).
W przypadku, gdy rozpatrywany punkt M leży pod obrysem powierzchni prostokątnej należy podzielić
tak powierzchnię prostokątną, aby punkt ten stanowił naroże nowo utworzonych prostokątów i posłużyć
się następującym schematem:
L
L1
A
L z 
η nMHAB = f  1 , 
 B1 B1 
L2
B
C
B1
M
H
B
D
B2
G
F
σ z = q ⋅ (ηnMHAB + ηnMBCD + η nMDEF + η nMFGH )
E
L z 
η nMBCD = f  2 , 
 B1 B1 
L z 
η nMDEF = f  2 , 
 B2 B2 
L z 
η nMFGH = f  1 , 
 B2 B2 
10
Zastosowanie metody punktów narożnych do obliczania naprężeń
pionowych w dowolnym miejscu półprzestrzeni gruntowej (2).
W przypadku, gdy rozpatrywany punkt M leży poza obrysem powierzchni prostokątnej należy
wprowadzić dodatkowe powierzchnie prostokątne w taki sposób, aby punkt ten stanowił naroże nowo
powstałych prostokątów i posłużyć się następującym schematem:
L
L1
H
L2
L z 
η nMFGH = f  1 , 
 B2 B2 
M
D
B z 
η nMDEF = f  2 , 
 L2 B2 
B1
A
B
C
B2
L z 
η nMBAH = f  1 , 
 B1 B1 
B
G
L z 
η nMDCB = f  2 , 
 B1 B1 
E
F
σ z = q ⋅ (ηnMFGH + η nMDEF − η nMBAH − η nMDCB )
Fundamenty budowli (podział)
FUNDAMENTY BUDOWLI
FUNDAMENTY PŁYTKIE
(bezpośrednie)
•Stopy fundamentowe
•Ławy fundamentowe
•Płyty
•Ruszty
•Skrzynie
FUNDAMENTY GŁĘBOKIE
(pośrednie)
•Pale
•Studnie
•Kesony
11
Naprężenia pod fundamentem bezpośrednim
I. Stan przed rozpoczęciem budowy
Naprężenia pod fundamentem bezpośrednim
II. Stan po wykonaniu wykopu fundamentowego
Podziałka głębokości:
1m
Podziałka naprężeń:
γ1
D
20 kPa
h
z=0
γ1
z
zwg
γ
σ
σhhγ
m1
γ2'
m2
γ3'
m3
γ4'
m4
Podziałka głębokości:
1m
Podziałka naprężeń:
20 kPa
D
z=0
z
zwg
σz
σzm
m1
s
m2
m3
m4
12
Naprężenia pod fundamentem bezpośrednim
III. Stan po zasypaniu wykopu fundamentowego
Naprężenia pod fundamentem bezpośrednim
IV. Stan po wykonaniu obiektu budowlanego
Podziałka głębokości:
1m
Podziałka naprężeń:
20 kPa
D
z=0
B
z
zwg
σz
m1
s
m2
σzm
m3
m4
Q
Podziałka głębokości:
1m
Podziałka naprężeń:
20 kPa
D
q = Q/LB
z=0
B
z
zwg
σz
m1
s
σzd
σzm
σz
m2
t
m3
m4
13
Obliczanie osiadania fundamentów
Obliczanie osiadania zaleca się przeprowadzić metodą naprężeń. Osiadanie Si warstwy
należy wyznaczyć jako sumę osiadania wtórnego Si” w zakresie naprężenia wtórnego
σzs, z zastosowaniem modułu ściśliwości wtórnej gruntu M (lub modułu wtórnego
odkształcenia E, w zależności od metody obliczania), oraz osiadania pierwotnego Si’
w zakresie naprężenia dodatkowego σzd, z zastosowaniem modułu ściśliwości
pierwotnej gruntu Mo (lub Eo).
Osiadanie Si warstwy podłoża o miąższości mi oblicza się wg wzorów:
Si = Si' ' + Si'
Si' ' = λ
Si' =
Si"
S
σ ,σ
σ zid ⋅ mi
M oi
– osiadanie wtórne warstwy i, [cm],
'
i
s
zi
σ zis ⋅ mi
Mi
– osiadanie pierwotne warstwy i, [cm],
d
zi
Mi, Moi
– odpowiednio wtórne i dodatkowe naprężenie w podłożu pod fundamentem,
w połowie grubości warstwy, [kPa],
– edometryczny moduł ściśliwości, odpowiednio wtórnej i pierwotnej, ustalony dla
gruntu warstwy i, kPa,
mi – grubość warstwy i, cm,
λ
– współczynnik uwzględniający stopień odprężenia podłoża po wykonaniu
wykopu, którego wartość należy przyjmować:
λ=0
– gdy czas wznoszenia budowli (od wykonania wykopów fundamentowych do
zakończenia stanu surowego, z montażem urządzeń stanowiących obciążenie stałe)
nie trwa dłużej niż 1 rok,
λ=1
– gdy czas wznoszenia budowli jest dłuższy niż 1 rok.
Warstwy o grubości większej niż połowa szerokości B fundamentu należy dzielić dodatkowo
na części o miąższości nie przekraczającej 0.5B.
14
Całkowite osiadanie podłoża pod fundamentem bezpośrednim, a zatem osiadanie całej
budowli oblicza się sumując osiadania wszystkich warstw cząstkowych według wzoru:
n
S = ∑ Si
i =1
gdzie:
i – numer warstwy cząstkowej;
n – ilość warstw,
Si – osiadanie warstwy i–tej.
Q
Podziałka głębokości:
1m
Podziałka naprężeń:
20 kPa
D
q = Q/LB
z=0
B
z
zwg
m1
m2
m3/2
m3/2
σz3 σz3
s
d
S3
m3
m4
15
Wyznaczenie głębokości podłoża budowlanego (zmax)
Q
Podziałka głębokości:
1m
Podziałka naprężeń:
D
20 kPa
q = Q/LB
z=0
B
z
zwg
m1
0.3σhγ
σhγ
σzd
zmax
m2
m3
wykres naprężeń
pierwotnych
m4
σhγ
0.3σhγ
linia pomocnicza
0.3σhγ
16