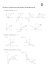Część IX

–
Materiały dydaktyczne na zajęcia wyrównawcze z matematyki
dla studentów pierwszego roku kierunku zamawianego
Inżynieria Środowiska
w ramach projektu „Era inżyniera – pewna lokata na przyszłość”
Projekt „Era inżyniera – pewna lokata na przyszłość” jest współfinansowany
przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
Funkcja logarytmiczna
9. Funkcja logarytmiczna
1. Logarytmy.
Niech a ∈ R+ \ {1}, b ∈ R+ . Logarytmem liczby b przy podstawie a nazywamy liczbę c wtedy
i tylko wtedy, gdy ac = b. Piszemy
loga b = c ⇐⇒ b = ac .
loga 1 = 0
loga a = 1
aloga b = b
log = log10 a – logarytm dziesiętny
ln a = loge a – logarytm naturalny
Działania na logarytmach
loga (b1 · b2 ) = loga b1 + loga b2 ,
(e ≈ 2, 718281828)
a ∈ R+ \ {1}, b1 , b2 ∈ R+
loga ( bb12 ) = loga b1 − loga b2 , a ∈ R+ \ {1}, b1 , b2 ∈ R+
loga bm = m loga b,
a ∈ R+ \ {1}, b ∈ R+ , m ∈ R
loga b =
logc b
logc a ,
a, c ∈ R+ \ {1}, b ∈ R+
loga b =
1
logb a ,
a, b ∈ R+ \ {1}
2. Funkcja logarytmiczna.
Funkcja logarytmiczna to funkcja postaci f (x) = loga x, gdzie a ∈ R+ \ {1}, x ∈ R+ .
WŁASNOŚCI:
• dziedzina R+ ;
• zbiór wartości R;
• funkcja różnowartościowa;
• funkcja ciągła;
• funkcja odwrotna do funkcji wykładniczej o tej samej podstawie;
• jeśli a > 1, to funkcja jest rosnąca;
• jeśli 0 < a < 1, to funkcja jest malejąca.
40
Funkcja logarytmiczna
3. Równanie logarytmiczne
Jeżeli f (x) > 0, g(x) > 0, a ∈ R+ \ {1}, to
loga f (x) = b ⇐⇒ f (x) = ab .
lub
loga f (x) = loga g(x) ⇐⇒ f (x) = g(x).
4. Nierówności logarytmiczne
Jeśli 0 < a < 1, to
loga f (x) > loga g(x) ⇐⇒ f (x) < g(x).
Jeśli 0 < a < 1, to
loga f (x) > loga g(x) ⇐⇒ f (x) 6 g(x).
Jeśli a > 1, to
loga f (x) > loga g(x) ⇐⇒ f (x) > g(x).
Jeśli a > 1, to
loga f (x) > loga g(x) ⇐⇒ f (x) > g(x).
Przykładowe zadania
1. Obliczyć log2 32.
Rozwiązanie:
log2 32 = log2 25 = 5 log2 2 = 5
Odpowiedź: 5.
2. Obliczyć log 1 27.
3
Rozwiązanie:
log 1 27 = log 1 33 = log 1
3
3
3
( )−3
1
3
= −3
Odpowiedź: −3.
3. Obliczyć log3 5 · log25 81.
Rozwiązanie:
log3 5 · log25 81 = log3 5 ·
log3 81
log3 25
= log3 5 ·
log3 34
log3 52
= log3 5 ·
4 log3 3
2 log3 5
=
4
2
=2
Odpowiedź: 2.
4. Obliczyć 4log2 3 .
Rozwiązanie:
2
4log2 3 = (22 )log2 3 = 22 log2 3 = 2log2 3 = 32 = 9
Odpowiedź: 9.
41
Funkcja logarytmiczna
5. Rozwiązać równanie log4 x = 3.
Rozwiązanie:
Założenia: x > 0.
Z definicji logarytmu otrzymujemy
x = 43 = 64
Odpowiedź: x = 64.
6. Rozwiązać równanie log2 (x + 1) + log2 (x + 3) = 3.
Rozwiązanie:
Założenia: x + 1 > 0, czyli x > −1 oraz x + 3 > 0,czyli x > −3. Zatem D = (−1, +∞).
Korzystamy ze wzoru loga (x · y) = loga x + loga y
log2 ((x + 1)(x + 3)) = 3
Z definicji logarytmu
(x + 1)(x + 3) = 23
x2 + 4x − 5 = 0
∆ = 36, x1 = −5 ∈
/ D, x2 = 1
Odpowiedź: x = 1.
7. Rozwiązać równanie log4 (x + 3) − log4 (x − 1) = 2 − log4 8.
Rozwiązanie:
Założenia: x + 3 > 0, czyli x > −3 oraz x − 1 > 0, czyli x > 1. Zatem D = (1, +∞).
Korzystamy ze wzoru loga ( xy ) = loga x − loga y oraz x = loga ax
2
log4 x+3
x−1 = log4 4 − log4 8
16
log4 x+3
x−1 = log4 8
log4 x+3
x−1 = log4 2
x+3
x−1 = 2
x + 3 = 2(x − 1)
x=5
Odpowiedź: x = 5.
8. Rozwiązać równanie log3 (x2 + 4x + 12) = 2.
Rozwiązanie:
Założenia: x2 + 4x + 12 > 0, ∆ = −32 < 0, D = R.
Z definicji logarytmu
x2 + 4x + 12 = 32
x2 + 4x + 3 = 0
∆ = 4, x1 = −3, x2 = −1
Odpowiedź: x ∈ {−3, −1}.
9. Rozwiązać równanie
2 log x
log(5x−4)
= 1.
Rozwiązanie:
Założenia: x > 0 oraz 5x − 4 > 0, czyli x >
x ̸= 1
42
4
5
oraz log(5x − 4) ̸= 0, log(5x − 4) ̸= log 1, 5x − 4 ̸= 1,
Funkcja logarytmiczna
Zatem D = ( 45 , +∞) \ {1}.
Mnożymy obie strony przez log(5x − 4)
2 log x = log(5x − 4)
log x2 = log(5x − 4)
x2 = 5x − 4
x2 − 5x + 4 = 0
∆ = 9, x1 = 1 ∈
/ D, x2 = 4
Odpowiedź: x = 4.
10. Rozwiązać nierówność log2 (x + 2) > 3.
Rozwiązanie:
Założenia: x + 2 > 0, czyli x > −2, zatem D = (−2, +∞).
Korzystamy ze wzoru loga bm = m loga b
log2 (x + 2) > log2 23
x + 2 > 8, czyli x > 6
Po uwzględnieniu dziedziny otrzymujemy, że x ∈ (6, +∞).
Odpowiedź: x ∈ (6, +∞).
11. Rozwiązać nierówność log 1 (x − 1) < 2.
2
Rozwiązanie:
Założenia: x − 1 > 0, czyli x > 1, zatem D = (1, +∞).
Korzystamy ze wzoru loga bm = m loga b
( )2
log 1 (x − 1) < log 1 12
2
2
x − 1 > 14 (bo 12 ∈ (0, 1))
x > 54
(
)
Po uwzględnieniu dziedziny otrzymujemy x ∈ 54 , +∞
Odpowiedź: x ∈
(
5
4 , +∞
)
.
12. Rozwiązać nierówność log3 (2x − 7) 6 2 − log3 (8 − x).
Rozwiązanie:
Najpierw wyznaczamy dziedzinę:
2x − 7 > 0, czyli x > 72 oraz 8 − x > 0, czyli x < 8. Zatem D = ( 72 , 8).
log3 (2x − 7) + log3 (8 − x) 6 2
Korzystamy ze wzoru loga (x · y) = loga x + loga y oraz loga ak = k
log3 ((2x − 7)(8 − x)) 6 2
log3 ((2x − 7)(8 − x)) 6 log3 32
16x − 2x2 − 56 + 7x 6 9
−2x2 + 23x − 65 6 0
2x2 − 23x + 65 > 0
∆ = 9, x1 = 5, x2 = 13
2
x ∈ (−∞, 5] ∪ [ 13
,
+∞)
2
] [
)
(
,
8
.
Po uwzględnieniu dziedziny x ∈ 72 , 5 ∪ 13
2
43
Funkcja logarytmiczna
Odpowiedź: x ∈
(
]
7
2, 5
∪
[
x
13
2
5
)
13
2 ,8
.
13. Rozwiązać nierówność log2x−3 x > 1.
Rozwiązanie:
Najpierw wyznaczamy dziedzinę:
Założenie: x > 0 oraz 2x − 3 > 0, czyli x > 23 oraz 2x − 3 ̸= 1, czyli x ̸= 2. Zatem
D = ( 23 , 2) ∪ (2, +∞).
Rozważamy dwie sytuacje: gdy podstawa logarytmu jest większa od 1 lub gdy jest z przedziału
(0, 1).
a) 2x − 3 > 1, czyli x > 2 – wtedy funkcja logarytmiczna jest rosnąca, zatem
log2x−3 x > log2x−3 (2x − 3)
x > 2x − 3, czyli x < 3
Po uwzględnieniu założeń x ∈ (2, 3).
b) 0 < 2x − 3 < 1, czyli 3 < 2x < 4, więc 32 < x < 2 – wtedy funkcja logarytmiczna jest malejąca,
zatem
log2x−3 x > log2x−3 (2x − 3)
x < 2x − 3
(
)
x > 3 – nie należy do przedziału 32 , 2
Odpowiedź: x ∈ (2, 3).
Zadania
Obliczyć:
1. log3
1
27 .
2. log 1 9.
3
3. 2log16 5 .
1
√
7. ( 3 9) 5 log5 3 .
4. log8 1.
5. 49log7 2 .
√
6. log 1 3 3 3.
8. 42+log4 7 .
9. log36 24, gdy log2 6 = a.
9
Rozwiązać równanie:
(
)
10. log(2 − x) = log(x + 3).
16. log3 log5 (2x + 1) = 0.
11. log 1 (15 − x) = 8.
17. logx−2 9 = 2.
12. log3 (x + 5)2 = 1.
18. log2 x = 6 + log x.
13. log3 (x2 + x + 3) = 2.
19.
14. log 1 (2x + 3) = −2.
20. logx 2 − 4 log2 x = 3.
15. log x + log(x + 3) = 1.
21. | log2 (3x − 1) − log2 3| = | log2 (5 − 3x) − 1|.
3
4
44
2 log x
log(5x−4)
= 1.
Funkcja logarytmiczna
Rozwiązać nierówność:
(
22. log
x2 −4x+5
x−1
)
6 0.
29. logx 25 < 5.
23. log2 (x + 2) + log2 (x + 14) < 6.
30. logx+5 x > 1.
24. log23 x − 1 < 0.
31. log20,1 x − 5 log0,1 x − 6 6 0.
25. log3 (x2 + 2) > 3.
32. | log x| < 2.
26. log 1 (x − 3) < −2.
33. |3 log x − 1| < 1.
27. log2x−5 (x − 1) > 1.
34. log x−1
x+1 < 3.
28. log 1 log4 (x2 − 5) > 0.
35. log 1 |x − 3| < −2.
4
(
)
3
4
Naszkicować wykresy funkcji:
38. f (x) = | log 1 (x + 1)|.
36. f (x) = log(−x) + 2.
2
37. f (x) = − log2 (x − 2) + 3.
39. f (x) = −| log 1 (x + 2) − 1|.
5
Wyznaczyć dziedzinę funkcji:
40. f (x) = log(x2 − 4) +
√
log(9−x2 )
41. f (x) =
.
3x −1
42. f (x) =
√
√
6 − 2x.
log 1 (x − 3) − 1.
2
2
43. f (x) =
√
logx (3 − x).
44. f (x) = log2 (1 − log 1 (x2 − 5x + 6)).
2
45. f (x) =
1
log3 x
−
10
2−log3 (x+1) .
45