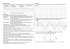
81. Fala poprzeczna ( , )= sin y x t A t k x ω ⋅ − ⋅ o długości λ = 1,56

WM-E; kier. MBM, lista zad. nr 12 pt. (z karty przedmiotu): Analiza i rozwiązywania zadań z zakresu dynamiki ruchu
drgającego: harmonicznego prostego, tłumionego, wymuszonego i rezonansu mechanicznego. Rozwiązywanie zadań
z zakresu fizyki fal mechanicznych i akustycznych i obliczanie wartości podstawowych wielkości ruchu falowego. Lista ma na
celu zdobycie przez studentów wiedzy matematyczno-fizycznej, nabycie umiejętności rozwiązywania prostych zadań
dotyczących dynamiki ruchów drgających, ruchu falowego i utrwalanie dotychczas zdobytej wiedzy fizycznej.
81. Fala poprzeczna y ( x, t ) = A sin (ω ⋅ t − k ⋅ x ) o długości λ = 1,56 m, A = 2·10-5 m biegnie w naciągniętej
strunie o liniowej gęstości masy 10-4 kg/m. Punkty struny przebywają dystans od położenia równowagi do
maksymalnego wychylenia (odkształcenia) w czasie 0,5 ms. Oblicz: okres, częstotliwość, prędkość tej
fali, siłę naciągu struny, maksymalną prędkość i maksymalne przyspieszenie ruchu drgającego
dowolnego elementu struny. Napisz jawną postać matematyczną tej fali stosując jednostki SI.
82. Kosinusoidalna fala rozchodzi się w sprężynie leżącej na osi OX. Amplituda fali A = 0,01m, długość
λ = 0,4m, a częstotliwość f = 8 Hz. Poprzeczne wychylenie punktów sprężyny dla t = 0 i x = 0 wynosi
0,01m.Wyznaczyć wektor falowy k, okres T, częstość kołową ω, prędkość c, fazę początkową tej fali.
Napisz równanie tej fali.
83. Fala podłużna u( x, t ) = 3 ⋅ 10−6 cos ( 4 ⋅ 103π t − 0,8π x ) biegnie w stalowym pręcie o gęstości masy 7900
kg/m3 i polu przekroju porzecznego 4·10-4 m2. Ile wynosi: a) średnia energia wnoszona przez falę do
fragmentu ośrodka o długości ∆x = 0,001 m, b) średnia moc fali, (c) średnia intensywność fali, (d) średnia
gęstość energii fali w pręcie, (e) ciśnienie, jakie wywiera ta fala na ściankę, do której jest przymocowany
pręt, gdy fala odbija się całkowicie od ściany. Ws-ka: Patrz zad 23-26 poniżej.
84. A) W skorupie ziemskiej fale podłużne mają prędkość c = 8 km/s a fale poprzeczne c⊥ = 4,5 km/s .
Stacja sejsmograficzna zarejestrowała oba typy fal wywołane trzęsieniem ziemi, przy czym fale podłużne
odebrała o 18 min wcześniej. Oszacuj w jakiej odległości od stacji znajdowało się epicentrum trzęsienia
ziemi? B) Kamień wrzucono do głębokiej studni. Po upływie t sekund usłyszano plusk. Czy można
wyznaczyć głębokość studni? Jakie dane są do tego niezbędne?
85. Monochromatyczna fala akustyczna pada pod kątem α na powierzchnię wody. Dla jakich kątów
padania fala ta nie wnika do wody? Prędkość dźwięku w wodzie c2 =1500 m/s, a w powietrzu c1 = 332
m/s; prawo załamania dla fal akustycznych c2 ⋅ sin α = c1 ⋅ sin β , gdzie β − kąt załamania. Komentarz:
Zaskakujący na pozór wynik, bowiem powinno być tak, jak w optyce geometrycznej: Fala przechodząca z
ośrodka rzadszego do gęstrzego nie powinna ulegać całkowitemu wewnętrznemu odbiciu!
86. Podaj regułę wyznaczania odległości w kilometrach od miejsca błyskawicy metodą zliczania sekund
upływających od zobaczenia błysku do usłyszenia grzmotu. Załóż, że dźwięk biegnie po linii prostej.
87. Dwóch kibiców piłki nożnej obserwuje mecz i widzi kopnięcie przez piłkarza piłki. Dźwięk
uderzonej piłki dociera do obu z opóźnieniami 0,25 s i 0,14 s. Linie proste poprowadzone od kibiców do
piłkarza tworzą kąt prosty. W jakiej odległości od siebie znajdują się kibice?
88. Umocowana dwustronnie struna skrzypiec o długości 15 cm wydaje ton podstawowy. Prędkość
dźwięku w strunie 250 m/s, a w powietrzu 332 m/s. Obliczyć częstość i długość rozchodzącego się
dźwięku w strunie i w powietrzu.
89. Zamocowana na obu końcach lina ma długość 8.4 m i masę 0,12 kg. Lina została naciągnięta siłą 96
N i wprawiona w drgania. Wyznacz: (a) prędkość fali w linie; (b) największą możliwą długość fali
stojącej i podaj częstość tej fali.
90. Opracuj i włącz do portfolio pisemny esej/opracowanie nt. zastosowań ultradźwięków (w technice,
technologii, produkcji, medycynie itp.); esej powinien liczyć co najmniej 6 tys. znaków bez spacji; źródła literaturowe należy znaleźć samodzielnie; esej/opracowanie nie może mieć znamiona plagiatu, co jest dzisiaj
traktowane jako przestępstwo.
W. Salejda
Wrocław, 1 grudnia 2015
1
Siłownia umysłowa. Zadania przeznaczone do samodzielnego rozwiązania
1. Napisz równanie opisujące poprzeczną falę sinusoidalną biegnącą w sznurze w dodatnim kierunku osi OX, dla której k = 60
cm−1, T = 0,2 s, A = 3mm. Wyznacz maksymalną prędkość poprzeczną cząsteczek sznura. Jak wyznaczamy współrzędne
punktów sznura, w których w danej chwili wychylenie jest maksymalne/zerowe?
2. Po naciągniętej strunie biegnie fala poprzeczna y ( x , t ) = 0, 024 ⋅ sin [ 3 ⋅ x + 40 ⋅ t ] . Liniowa gęstość masy tej struny
wynosi 2.2·10-4 kg/m. Oblicz prędkość fali i naprężenie struny.
3. Fala poprzeczna biegnąca w sznurze ma postać (w SI) y( x, t ) = 0,35 ⋅ sin (10π t − 6π x + π / 4) . Ile wynosi prędkość c i jaki jest
kierunek rozchodzenia się tej fali? Jakie jest wychylenie punktów ośrodka dla t = 0 i x = 0,1 m? Ile wynosi długość i
częstotliwość tej fali? Ile wynosi maksymalna wartość prędkości poprzecznej?
4. Dwie fale biegnące opisują równania (w SI): y1 = 0,3 sin[π(5x−200t)] oraz y2 = 0,3 sin[π(5x−200t)+π/3]. W wyniku ich
nałożenia powstaje fala biegnąca. Wyznaczyć amplitudę, prędkość i długość fali biegnącej.
5. Struna ma długość 1,5 m, masę 8,7 g, a jej naprężenie wynosi 120 N. Zamocowano jej końce i wzbudzono drgania.
Obliczyć: (a) prędkość rozchodzenia się fal poprzecznych w tej strunie; (b) długość i częstotliwość dwóch fal interferujących
ze sobą i wytwarzających na strunie falę stojącą o: b1) jednej strzałce; b2) dwóch strzałkach. Jakie są długości fal akustycznej,
których źródłem jest ta struna?
6. Jednorodna struna o masie m i długości L zwisa pionowo w dół. Pokazać, że prędkość fali poprzecznej w tej strunie zależy
od odległości y od dolnego końcu jak c(y) = (gy)1/2. Ile wynosi czas potrzebny fali poprzecznej na przebycie odległości od
dolnego do górnego końca struny? Rozwiązanie: Na element struny o długości ∆y odległy od dolnego końca struny o y działa
siła naciągu N(y) = ρ·y·g będąca ciężarem struny o długości y, gdzie ρ = m/L. Dla y = L wartość siły naciągu jest równa
ciężarowi struny i wynosi N(y = L) = m·L·g/L = mg. Prędkość fali wyraża się wzorem c ( y ) =
N ( y ) ρ , z którego po
1/2
prostych podstawieniach i uproszczeniach otrzymujemy c(y) = (gy) . Na przebycie drogi ∆y fala potrzebuje czasu ∆t =
∆y/c(y), tj. ∆t =
∆y
=
c ( y)
jest sumą czasów ∆t =
sumę T =
∆y
N ( y) ρ
=
∆y
; całkowity czas przebiegu fali wzdłuż struny od jej jednego do drugiego końca
gy
∆y
, gdy wartość y zmienia się od zera do L a ∆y zmierza do zera, innymi słowy, należy policzyć
gy
y=L
∆y
, co prowadzi do końcowego wyniku
gy
∑ ∆t = lim ∆y→0 ∑
y =0
T =∫
L
0
1
dy
=
gy
g
∫
L
0
2
dy
=
y
g
y 0L =
2
g
(
)
L− 0 =2
L
.
g
7. Dwie fale y1(x, t) = 4,0·10-3sin(3,0x − 20t) oraz y2(x, t) = 8,0·10-3cos(3,0x − 20t) rozchodzą się jednocześnie w ośrodku
sprężystym. Pokaż, że wypadkowa fala y(x, t) = y1(x, t)+y2(x, t) jest także falą sinusoidalną oraz oblicz jej fazę i amplitudę.
Rozwiązanie: Niech α(t) = 3,0x − 20t. Wypadkowa fala y(x, t) = 4,0 sin α(t) + 8,0 cos α(t); z drugiej strony ma mieć ona
postać y(x, t) = Asin[α(t) + β], gdzie β = const — faza początkowa. Porównując oba wyrażenia i stosując tożsamość sin(α + β)
= sinα cos β + sin β cos α, otrzymujemy układ równań {Acos β = 4, Asin β = 8}, z którego mamy A2 (sin2 β + cos2 β) = 42 + 82
i dalej A = 4√5, oraz tg β = 2, co dla sin β > 0 i cos β > 0 daje β = arc tg 2 ≈ 63o.
8. Wyznaczyć prędkość poprzeczną v = ∂y/∂t oraz przyspieszenie poprzeczne a = ∂2y/∂t2 fragmentów struny w chwili czasu t =
0,2 s w punkcie x = 1,6m struny, w której rozchodzi się fala y(x, t) = 0,12 sin[π(x/8 + 4t)]. Ile wynoszą wartości maksymalne
wyznaczonych wielkości? Dla jakich chwil czasu wielkości v oraz a osiągają w tym punkcie wartości ekstremalne? Czy
spełniona jest relacja a = −ω2y? Ile wynoszą: długość, okres i prędkość fazowa tej fali?
9. Sprawdzić, że równanie fali kosinusoidalnej y(x, t) = Acos(ωt − kx), gdzie ω/c = k = 2π/λ jest rozwiązaniem
jednowymiarowego równania falowego ∂2y/∂t2 = c2∂2y/∂x2. Pokaż, że dla tej fali średnia prędkość cząsteczek ośrodka liczona
w czasie jednego okresu źródła fali jest równa zeru, tj. v ( x , t ) =
1
T
T
∫ ( − Aω sin (ω ⋅ t − k ⋅ x ) )dt = 0.
0
10. Prędkość dźwięku w powietrzu c = 332 m/s. Źródłem dźwięku o częstotliwości 300 Hz jest syrena wozu policyjnego. (a)
Wóz porusza się z prędkością 45 m/s. Obliczyć częstotliwość i długość fal przed i za wozem. (b) Za wozem jadą dwa
samochody: jeden w tym samym kierunku z prędkością 30 m/s, a drugi w przeciwnym kierunku z prędkością 15m/s. Jakie
częstości fal słyszą pasażerowie samochodów? (c) Wóz policyjny zbliża się z prędkością 5m/s do pionowej ściany odbijającej
dźwięk syreny. Jaką częstotliwość dudnień słyszy policjant? Ws-ka do zad. (c): Wyznacz najpierw częstotliwość dźwięku
docierającego do ściany (i odbijającego się od niej) – ściana jest źródłem/nadajnikiem fali odbieranej przez policjantów, a
następnie częstotliwość fali odbieranej przez policjantów. Należy pamiętać o tym, że częstotliwość odbieranej fali akustycznej
zależy zarówno od prędkości detektora/odbiornika jak i od źródła/nadajnika względem powietrza i liczona jest ze wzoru. Jeśli
skierujemy wektor Rdetektor→źródło o początku w miejscu położenia detektora i o zwrocie od detektora do źródła, to częstość
odbieranej fali przez odbiorcę określa wzór f detektora/odbiornika = f źródla/nadajnika
c ± vdetektora/odbiornika
; znaki plus wybieramy pod
c ± vźródla/nadajnika
warunkiem, że prędkości mają zwroty zgodne z dodatnim zwrotem wektora Rdetektor→źródło.
2
11. Akustyczny alarm przeciwwłamaniowy samochodu emituje falę o częstości 10 kHz. Jaka jest częstość dudnień
powstających po nałożeniu się fali alarmu i fali odbitej od intruza, tj. potencjalnego złodzieja, oddalającego się od źródła z
prędkością 3m/s? Prędkość dźwięku 332 m/s.
12. Podwodne okręty Czerwony Październik (CP) i Blue Shark (BS) płyną naprzeciw siebie po tym samym kursie w
nieruchomej wodzie oceanu. Ich prędkości wynoszą: vCP = 50 km/h, vBS = 70 km/h. CP wysyła sygnały sonaru o częstotliwości
1 kHz, których prędkość w wodzie wynosi 5470 m/s. Jaka jest częstotliwość
częstotliwość
BS
f odb.
sygnałów odbieranych przez BS? Jaka jest
CP
CP
f odb.
odbieranych na pokładzie CP fal odbitych od BS? Jak mierząc f odb. wyznaczamy (nie znając prędkości
VBS) prędkość BS? Rozwiązanie. Równanie, które pozwala wyznaczyć nieznaną prędkość xBS = vBS ma postać
CP
CP
f odb.
= f nad
CP
CP
c + xBS c + vCP
c ⋅ ( c − vCP ) ⋅ f odb.
− f nad
⋅ ( c + vCP ) ⋅ c
⋅
→ xBS =
.
CP
CP
c − vCP c − xBS
f nad ⋅ ( c + vCP ) + ( c − vCP ) f odb.
Wniosek: Za pomocą sonaru CP może namierzać cudzy okręt podwodny i zmierzyć jego prędkość. Wyprowadzenie powyższego
wzoru. BS odbiera sygnał (patrz zadanie 151.) o częstotliwości (uwaga, v [m/s] = v [km/h]/3,6)
c + vBS
≃ 1,1048 kHz. Fale te odbijają się od BS, który staje się ruchomym źródłem fal sprężystych dla CP
c − vCP
CP
BS c + vCP
odbieranych z częstością f odb. = f odb.
≃ 1,2226 kHz. Traktując vBS jako niewiadomą, możemy wyznaczyć ją w
c − vBS
BS
CP
f odb.
= f nad
oparciu o dane będące w dyspozycji CP, ponieważ
CP
BS
f odb.
= f odb.
CP
CP
f odb.
= f nad
c + vCP
,
c − v BS
BS
CP
f odb.
= f nad
c + v BS c + vCP
⋅
,
c − vCP c − v BS
CP
CP
f odb.
= f nad
c + vBS
,
c − vCP
c + x BS c + vCP
⋅
,
c − vCP c − x BS
CP
CP
= f nad
( c − vCP )( c − xBS ) f odb.
( c + xBS ) ⋅ ( c + vCP ) →
CP
CP
CP
CP
− ( c − vCP ) ⋅ xBS ⋅ f odb.
+ c ⋅ ( c − vCP ) ⋅ f odb.
= f nad
⋅ ( c + vCP ) ⋅ xBS + f nad
⋅ ( c + vCP ) ⋅ c →
i kolejno otrzymujemy :
CP
CP
CP
CP
c ⋅ ( c − vCP ) ⋅ f odb.
− f nad
⋅ ( c + vCP ) ⋅ c = f nad
⋅ ( c + vCP ) ⋅ xBS + ( c − vCP ) ⋅ xBS ⋅ f odb.
→
xBS = vBS
vBS =
CP
CP
c ⋅ ( c − vCP ) ⋅ f odb.
− f nad
⋅ ( c + vCP ) ⋅ c
=
→ podstawiamy i liczymy
CP
CP
f nad
⋅ ( c + vCP ) + ( c − vCP ) f odb.
( 332m/s ) ⋅  332m/s −
50
50



m/s  ⋅ 1,2226 ⋅ 103 Hz − 103Hz ⋅ ( 332m/s ) ⋅  332m/s +
m/s 
3,6
3,6



→
50
50




103Hz ⋅  ( 332m/s ) +
m/s  +  ( 332m/s ) −
m/s  ⋅ 1,2226 ⋅ 103Hz
3,6
3,6

 

129122,318 − 114835,111
xBS = vBS =
≃ 19, 45m/ s = 70 km/ h.
345,8889 + 388,9226
Wniosek: Kapitan CP zna prędkość BS, którą wyznacza oprogramowanie sonaru na podstawie własnej prędkości oraz
zmierzonych wartości częstotliwości wysyłanych i odbieranych przez sonar.
13. Studnia rezonuje przy najniższej częstości 7Hz. Jak głęboka jest ta studnia?
14. Otwarta obustronnie piszczałka organowa A ma częstość podstawową 300 Hz (dla n = 1). Trzecia harmoniczna piszczałki
organowej B (dla n = 3), mającej jeden koniec otwarty, ma taką samą częstość, jak druga harmoniczna piszczałki A.
Wyznaczyć długości obu piszczałek.
15. Natężenie fali akustycznej w powietrzu wynosi I = (∆pmax)2/(2ρc), gdzie (∆pmax) ‒ amplituda zmian ciśnienia. Oszacować
wartość (∆pmax) dla dźwięku o częstotliwości 4 kHz i intensywności I = 10−8 W/m2. Jakie ciśnienie wywiera ta fala padając
prostopadle na powierzchnię, która: a) całkowicie pochłania, b) całkowicie odbija dźwięk?
16. Poziom głośności L fali dźwiękowej L = 10 lg(I/I0), gdzie I0 = 10−12W/m2. Wyznaczyć, ile razy większa jest amplituda
zmian ciśnienia dźwięku o poziomie głośności L = 100 dB od amplitudy zmian ciśnienia fali akustycznej L0 = 0? Ile wynosi
(∆pmax) dla tego dźwięku, jeśli I = (∆pmax)2/(2ρc)? (B) Poziom głośności źródła dźwięku wzrósł o 30 dB. O jaki czynnik
wzrosły jego natężenie oraz amplituda zmian ciśnienia ośrodka?
3
17. Głośniki A i B umieszczono na pionowym słupie, z których A znajduje się na wysokości Twoich uszu w odległości 3,75m
od nich, a B wisi na wysokości 2m bezpośrednio nad A. Amplitudy dźwięków o zgodnej fazie (dźwięki koherentne)
docierające do Twoich uszu są takie same. Częstotliwość emitowanych dźwięków przez głośniki zmienia się od 20Hz do
20kHz. Jakie częstotliwości słyszysz słabo, a które słyszysz głośniej?
18. Dwa głośniki stoją na estradzie w odległości 3,35 m od siebie. Znajdujesz się w odległości 18,3m od pierwszego i 19,5 m
od drugiego. Akustyk zasila oba głośniki sygnałem koherentnym, którego częstotliwość zmienia się od 20Hz do 20 kHz.
Jakich częstości o trzech najmniejszych częstościach nie słyszysz, a które słyszysz najlepiej?
19. Fala sinusoidalna o długości 1,56 m biegnie w napiętej linie. Punkty liny przebywają drogę od swego położenia
równowagi do maksymalnego wychylenia (odkształcenia) w czasie 0,24 s. Oblicz okres, częstotliwość i prędkość tej fali.
20. Równanie fali poprzecznej propagującej się wzdłuż naciągniętej długiej struny ma postać (w SI)
y ( x , t ) = 0,04 cos [0,05π ⋅ x + 6π ⋅ t ]. Wyznacz lub oblicz: amplitudę, długość, częstotliwość, prędkość fazową, kierunek
rozchodzenia się fali, maksymalną prędkość poprzeczną elementów struny. Jakie jest wychylenie elementów struny o
współrzędnej x = 0,038 m w chwili t = 0,37 s?
21. Liniowa gęstość masy struny wynosi 2,2·10-4 kg/m. Po tej strunie biegnie fala (w SI) y ( x , t ) = 0,024sin [ 3 ⋅ x + 40 ⋅ t ].
Podaj/oblicz: prędkość fali i naprężenie struny.
22. Fala poprzeczna biegnąca w sznurze ma postać (w SI) y ( x, t ) = 0,35sin(10π t − 3π x + π /4). Ile wynosi prędkość c i jaki
jest kierunek rozchodzenia się tej fali? Jakie jest wychylenie punktów ośrodka dla t = 0 i x = 0,1 m? Ile wynosi długość i
częstość tej fali? Ile wynosi maksymalna wartość prędkości poprzecznej?
23. Fala podłużna biegnąca w stalowym pręcie o gęstości 7900 kg/m3 i polu przekroju porzecznego 4·10-4 m2 postaci (w SI)
u( x, t ) = 3 ⋅ 10−6 ⋅ cos(4 ⋅ 103π t − 0,8π x ). Ile wynosi średnia energia fali we fragmencie ośrodka o długości ∆x = 0,001 m? Wska: Posłużyć się wzorem 〈∆Emech 〉 = ( ρ S ∆x )(ω A)2 / 2.
24. Ile wynosi średnia moc fali z zadania 23? Ws-ka. Skorzystać ze wzoru 〈∆W 〉 = ρ S ⋅ c(ω ⋅ A)2 / 2.
25. Ile wynosi średnia intensywność fali z zadania 23? Ws-ka: Wykorzystać wzór 〈 I 〉 = ρ ⋅ c ⋅ (ω ⋅ A) 2 / 2.
26. Ile wynosi średnia gęstość energii fali w pręcie z zad. 23? Ws-ka: Stosowny wzór 〈 ρ E 〉 = ρ ⋅ A2ω 2 / 2.
27. Jednorodna struna o masie m i długości L zwisa pionowo w dół. Pokazać, że prędkość fali poprzecznej w tej strunie zależy
od odległości y od dolnego końcu jak c = (gy)1/2. Ile wynosi czas potrzebny fali poprzecznej na przebycie odległości od
dolnego do górnego końca struny? Ws-ka: Na element struny ∆m odległy o y od dolnego jej końca działa siła Q(y) będąca
ciężarem struny o długości y o wartości Q(y) = ρ·y·g, gdzie ρ = m/L. Na przebycie drogi dy fala potrzebuje czasu dt = dy/c(y).
28. Jednorodna struna o masie m i długości L zwisa pionowo w dół. Do tej struny podwieszono masę M. Ile wynosi prędkość
fali poprzecznej w tej strunie w punkcie w odległości y od dolnego końcu. Ile wynosi czas potrzebny fali poprzecznej na
przebycie odległości od dolnego do górnego końca struny?
29.
30.
31. Wyznaczyć długości i częstości rezonansowe fal akustycznych w tubie o długości 0,57 cm wypełnionej powietrzem:
a) dwustronnie otwartej, b) jednostronnie zamkniętej.
34. Zamkniętą z obu stron rurę o dł. L=3m wypełniono nieznanym gazem, a następnie wytworzono w niej falę stojącą. Stwierdzono, że
czwarta częstość rezonansowa licząc od najniższej (podstawowej pierwszej) wyniosła f3=100 Hz. Jaka jest prędkość dźwięku w tym gazie?
35. Częstotliwość tonu podstawowego wydawanego przez strunę wynosi f0 = 200 Hz. Jak zmieni się częstotliwość tonu podstawowego, gdy
strunę skrócimy o 1/4 długości?
Wrocław, 1 grudnia 2015
W. Salejda
4