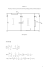Zadania rozwiązane

PRZYKŁAD 1
Wyznacz transformatę Laplace'a G(s) układu z poniŜszego rysunku(zerowe warunki
początkowe).
Rozwiązanie:
Zgodnie z drugą zasadą dynamiki Newtona:
ma = F
Czyli w naszym wypadku:
ma = F (t ) − Fk − Fc
Stąd
m&x&(t ) = F (t ) − kx(t ) − cx& (t )
Przekształcając:
m&x&(t ) + cx& (t ) + kx(t ) = F (t )
W celu wyznaczenia transmitancji układu zachodzi potrzeba „zasięgnięcia wiedzy” z
następnego rozdziału. Chodzi mianowicie o własność transformaty Laplace’a:
RóŜniczkowanie w dziedzinie rzeczywistej
_________________________________________________________________________________________________
1
®
Powered by xtoff
[email protected]
Własność tą wyraŜa się wzorem:
n −1
 d n f (t ) 
n
s n − k −1 f ( k ) (0)
£  dt n  = s F (s) − ∑
k =0


Czyli w tym wypadku równanie:
m&x&(t ) + cx& (t ) + kx(t ) = F (t )
Przy zerowych warunkach początkowych przyjmuje postać:
ms 2 X ( s ) + csX ( s ) + kX ( s ) = F ( s )
Zatem:
X ( s )(ms 2 + cs + k ) = F ( s )
Z czego wynika:
1
X ( s)
1
m
=
=
2
c
k
F ( s ) (ms + cs + k )
2
(s + s + )
m
m
Przeto:
G (s) =
X (s)
F ( s)
Ostatecznie więc transmitancja zadanego układu wynosi:
1
m
G (s) =
c
k
2
(s + s + )
m
m
_________________________________________________________________________________________________
2
®
Powered by xtoff
[email protected]
PRZYKŁAD 2
Wyznacz transformatę Laplace'a G(s) układu z poniŜszego rysunku(zerowe warunki
początkowe).
Rozwiązanie:
Rozwiązanie tego obwodu będzie wymagało zastosowania napięciowego prawa Kirchhoffa.
W lewym oczku moŜemy je zapisać jako:
− U r1 − U c + e = 0
W prawym zachodzi zaś zaleŜność:
−Ur2 +Uc −U L = 0
Korzystając ze znanych wzorów:
U r = iR
di
UL = L L
dt
du C
(*)
iC = C
dt
e = U WE
Otrzymujemy układ równań:
 − i1 R1 − U C + U WE = 0

diL
=0
− iL R2 + U C − L
dt

i1 = iC + i L

Po wyrugowaniu Uc oraz i1, otrzymujemy równanie:
di
− (iC + iL ) R1 − iL R2 − L L + U WE = 0
dt
Następnie podstawiając (*) i porządkując:
dU c
di
iL R1 + iL R2 + L L = 0 + U WE − CR1
(**)
dt
dt
_________________________________________________________________________________________________
3
®
Powered by xtoff
[email protected]
Następnie przekształcamy wzór:
−Ur2 +Uc −U L = 0
Do postaci:
UC = Ur2 +U L
Czyli:
dU C dU r 2 dU L
=
+
dt
dt
dt
Korzystając ze wzorów
U r = iR
di
UL = L L
dt
Otrzymano:
dU C
di
d 2i
= R2 L + L 2L
dt
dt
dt
Podstawiając do (**):
 diL
di L
d 2 iL 
= U WE − CR1  R2
+L 2 
iL ( R2 + R1 ) + L
dt
dt 
 dt
Stąd:
CR1 L
d 2 iL (t )
di (t )
+ (CR1 R2 + L) L + ( R2 + R1 )i L (t ) = U WE (t ) (***)
2
dt
dt
Korzystając z własności transformaty Laplace’a „RóŜniczkowanie w dziedzinie
rzeczywistej”:
n −1
 d n f (t ) 
n
s n − k −1 f ( k ) (0)
£  dt n  = s F (s) − ∑
k =0


I wiedząc, Ŝe warunki początkowe są zerowe, otrzymujemy:
CR1 Ls 2 I ( s ) + (CR1 R2 + L) sI ( s ) + ( R2 + R1 ) I ( s ) = U WE ( s )
Porządkując:
G (s) =
I (s)
1
=
2
U WE ( s ) CR1 Ls + (CR1 R2 + L) s + ( R2 + R1 )
_________________________________________________________________________________________________
4
®
Powered by xtoff
[email protected]
PRZYKŁAD 3
Przedstawić układ z poprzedniego zadania w funkcji stanu.
Rozwiązanie:
Zdefiniujmy zmienne stanu x1(t) i x2(t) jako:
x1 (t ) = iL (t )
dx (t ) di
x2 (t ) = 1 = L
dt
dt
Podstawiając do równania (***) otrzymujemy:
CR1 L
dx2 (t )
+ (CR1 R2 + L) x2 (t ) + ( R2 + R1 ) x1 (t ) = U WE (t )
dt
Porządkując:
dx1 (t )
= 0 + x2 (t )
dt
( R + R1 )
(CR1 R2 + L)
dx2 (t )
1
=− 2
x2 (t ) +
U WE (t )
x1 (t ) −
CR1 L
CR1 L
dt
CR1 L
Równania te zapisane w formie macierzowej:
 x&1   ( R 0+ R )
1
 x&  = − 2
 2  
CR1 L
1
 x
 0 
(CR1 R2 + L)   1  +  1 u
 
−
CR1 L   x2   CR1 L 
Stosując podstawienie y (t ) = i L (t ) moŜemy zapisać macierz wyjścia:
x 
y (t ) = [1 0] 1 
 x2 
_________________________________________________________________________________________________
5
®
Powered by xtoff
[email protected]