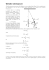. Ćwiczenie nr. 5 Wahadło matematyczne . Krótki opis fizyki ćwiczenia:

.
Ćwiczenie nr. 5
Wahadło matematyczne
M. Bielewski, E. Rulikowska
.
Krótki opis fizyki ćwiczenia:
Wahadło proste (matematyczne) jest to wyidealizowane ciało o masie punktowej m, zawieszone na cienkiej, nierozciągliwej i nieważkiej nici. Takie wahadło,
wyprowadzone z położenia równowagi, wykonuje ruch drgający w płaszczyźnie
pionowej pod wpływem siły ciężkości. Jest to ruch okresowy o okresie T . Na
rysunku 5.1 przedstawiono wahadło o długości l i masie m, odchylone od pionu
o kąt θ. Na masę m działa siła ciężkości mg i naprężenie nici N . Jako osie
współrzędnych przyjmujemy styczną do łuku (oś x) i przedłużenie promienia
nici (oś y). Siłę ciężkości mg rozkładamy na współrzędną radialną mg cos θ i
współrzędną styczną mg sin θ. Współrzędna styczna siły ciężkości wynosi
Rysunek 5.1: Wahadło matematyczne.
F = −mg sin θ.
Siła F nie jest więc proporcjonalna do przemieszczenia kątowego θ, ale do sin θ.
Dla małych kątów θ mamy sin θ ≈ θ1 , przemieszczenie masy m wzdłuż łuku wy1
θ[◦ ]
θ[rad]
2◦ 0, 03491 rad
5◦ 0, 08727 rad
10◦ 0, 17453 rad
sin θ
różnica w %
0, 03490
0, 03
0, 08716
0, 24
0, 17356
0, 50
nosi x = lθ i (znowu dla małych kątów θ) ruch jest w przybliżeniu prostoliniowy,
a siłę w nim działająca możemy zapisać jako
F = −mgθ = −mg
mg
x
=−
x.
l
l
Dla małych przemieszczeń siła F jest proporcjonalna do przemieszczenia ze
znakiem przeciwnym, czyli masa m wykonuje drgania harmoniczne proste. Stała mg/l jest odpowiednikiem stałej k w równaniu F = −kx, opisującym siłę
harmoniczną. Z teorii ruchu harmonicznego prostego, wiemy że okres takiego
ruchu wynosi
v
v
s
u
u m
ul
m
u
t
T = 2π
= 2π
= 2π t .
(5.1)
k
mg/l
g
Okres drgań wahadła prostego zależy więc jedynie od długości wahadła l oraz
od g (nie zależy od masy m wahadła). Można pokazać , że dla wahań o większej
amplitudzie wzór na okres ma postać
T =
v 
u
ul
2π t 1
g
1
+
2
!2
1·3
sin θm +
2·4
2
!2
1·3·5
sin θm +
2·4·6
4
!2

6
sin θm + . . .
(5.2)
W powyższym wzorze θm jest maksymalnym przemieszczeniem kątowym (zwykle wychyleniem początkowym), a kolejne wyrazy wewnątrz nawiasu są coraz
mniejsze. Wzór (5.1) dostajemy z powyższego wzoru przy zaniedbaniu wszystkich wyrazów w nawiasie za wyjątkiem jedności.