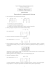1. Podaj postać standardowa Zadania Programowania

1. Podaj postać standardowa Zadania Programowania Liniowego
2. Sprowadź następujące zadanie programowania liniowego do postaci standardowej
Min -5x1 - 4x2
2x1 + x2 + x3 = 1
X1 + 4x2 – x4 = -2
-x1 + 3x2 – x5 = 1
X >= 0
3. Podaj definicję nieograniczonego zadania programowania liniowego.
4. Podaj definicję sprzecznego zadania programowania liniowego.
5. Podaj definicje rozwiązania bazowego zadania programowania liniowego w postaci
standardowej.
Rozwiązaniem bazowym układu równań Ax=b rz(A)=m, n>m
nazywamy wektor xb=B-1b utworzony ze zmiennych odpowiadających kolumnom aj
macierzy bazowej B. Składowe wektora bazowego xb to są zmienne bazowe.
6. Podaj definicje dopuszczalnego rozwiązania bazowego zadania programowania liniowego
w postaci standardowej.
Bazowym rozwiązaniem dopuszczalnym jest taki punkt wierzchołkowy zbioru punktów
dopuszczalnych zadania, w którym macierz AB jest nieosobliwa oraz ˆb ≥ 0
7. Dane jest następujące zadanie programowania liniowego
minx 5x1 + 4x2 + x4
2x1 + x2 + x4 = 1
x1 + 4x2 + x3 = −2
x1, x2, x3, x4 >=0
Określ jedno z rozwiązań bazowych tego zadania. Odpowiedz, czy jest to bazowe
rozwiązanie dopuszczalne.
B = {3,4} N = {1,2}
Zatem:
Ab = [0 1; 1 0], stąd b^ = [ -2 ; 1]
Nie jest to rozwiązanie bazowe dopuszczalne bo nie wszystkie zmienne bazowe są nieujemne.
B0 = {1, 4} , N0 = {3, 2} = {2, 3}
b^ nieformalnie z równań wybieramy gdzie x2 x3 = 0
b^ formalnie ze wzoru b^ = AB-1 * b
b^ = [1;2]
ceny niebazowe cn = [5;-2];
wyznaczamy zredukowane: cn^ = cn – AnT * Ab-T * cb
Sprawdzamy warunek stopu cn >= 0. Jeśli nie, to jedziemy dalej.
Wybieramy do wrzucenia: Najmniejsza z cen niebazowych.
Wybieramy do wyrzucenia: Gdy wybieramy co wyrzucić to konstruujemy zależności
zmiennych bazowych od wybranej zmiennej niebazowej (tej co wrzucamy) i patrzymy dla
jakiej jej wartości bazowe są równe 0. Wyrzucamy tą, dla której ta wartość (tej niebazowej)
jest mniejsza.
Rysujemy tabele:
Cn
|
0
5
-2
0
|-f^
-------------------------------------------------------------------X4
|
0
2
3
1
|2
X1
|
1
-1
2
0
|1
Mamy B = {4,1} N = {2,3}. Szukamy do wjebania: wybieramy x3 bo -2 najmniejsze z cen.
Szukamy do wyjebania:
• wybieramy 3-kolumne z A (bo x3 wjebujemy)
• z tej kolumny zajmujemy się tylko dodatnimi wyrazami
• dzielimy bi / ai3 i wybieramy z tych wyrażeń NAJMNIEJSZE (w naszym przypadku
2/3 vs. ½)
• ponieważ ½ jest mniejsze, to do wyjebania wybieramy x1 (czyli zamiana x1 na x3)
Tworzymy nowa tabele (musi być tak):
Cn
|
0
| -f^
-------------------------------------------------------------------X4
|
0
|
X3
|
1
|
Dodajemy cale wiersze miedzy sobą tak aby te zera nam się zrobiły i ta jedynka tez. Czyly:
Cn
|
1
4
0
0
| -f^ = -f(0,0,x3,x4) = 1
-------------------------------------------------------------------X4
|
-3/2 7/2
0
1
| 1/2
X3
|
1/2
-1/2 1
0
|½
Ponieważ cn > 0, to koniec.
Robimy simplex algebraiczny (ad. 8) do momentu aż trzeba wybrać, który element należy
wyrzucić i wtedy jeśli coś się pierdoli bo nie da się określić jednoznacznie, który element
wywalić – to zadanie jest nieograniczone.
CHYBA SIĘ KOMUŚ PIZNĘŁO SIĘ (GDZIE DO CHUJA 4 ZMIENNE!)
Zakładamy, że jest tylko x1 i x2.
Najpierw do postaci standardowej:
min 2x1 + x2
x1 + x2 – x3 = 2______\
1 1 -1 0 | 2
x1 + x2 + x4 = 1
/
1 2 0 1 | 1
b musi być większe równe zero!
Nie ma macierzy kanonicznej, wiec trzeba dojebać zmienną sztuczną x5 do równania
pierwszego, żeby razem z x4 tworzyły ją. Oto zadanie I fazy metody sympleks:
min x5
x1 + x2 – x3 + x5 = 2
x1 + x2 + x4 = 1
Cn
|
0
0
0
0
1
-------------------------------------------------------------X5
|
1
2
-1
0
1
X4
|
2
3
0
1
0
|-f^
------------|2
|1
Cn
|
-1
-2
1
0
0
-------------------------------------------------------------X5
|
1
2
-1
0
1
X4
|
2
3
0
1
0
|-f^
------------|2
|1
Cn
|
1/3
0
1
2/3
0
-------------------------------------------------------------X5
|
-1/3 0
-1
-2/3 1
X2
|
2/3
1
0
1/3
0
|-f^
------------|4/3
|1/3
Zmiennymi bazowymi jest {x5,x2} , a rozwiązaniem bazowym jest wektor [0,1,0,0,3]
jest to rozwiązanie dopuszczalne. Wartość funkcji celu w tym punkcie wynosi 4/3
Musimy naszą funkcję przekształcić do postaci takiej jak poniżej. W tym celu
zamieniamy x na –x i chyba gitara. Dalej jedziemy ze sztampy:
Zadanie dualne:
Jedziemy podobnie jak w zadaniu 14 ale jedziemy z następującej sztampy:
Zamieniamy ograniczenia:
X1 + 2x2 -1<=0
-2x1 – x2 +3 <=0
-2x1 +3x2 +2 <=0
Funkcja lagrange’a:
L(x,λ) = { x1 +2x2 + λ1( x1 + 2x2 -1) + λ2( -2x1 – x2 +3) + λ3(-2x1 +3x2 +2) }
Funkcja dualna:
LD(λ1,λ2,λ3,λ4) = infx∈R^2 {- λ1 +3 λ2+2 λ3 +x1(1+ λ1−2 λ2−2 λ3) +x2(2+2 λ1− λ2+3 λ3) } =
=
- λ1 +3 λ2+2 λ3 gdy 1+ λ1−2 λ2−2 λ3 = 0 i 2+2 λ1− λ2+3 λ3 = 0
-∞ w pozostałych przypadkach
Zadanie dualne:
Max - λ1 +3 λ2+2 λ3
p.o.
1+ λ1−2 λ2−2 λ3 = 0
2+2 λ1− λ2+3 λ3 = 0
λ >= 0
????
„jeżeli j-ta zmienna dualna ma wartość większą od zera, to odpowiadające jej ograniczenie
w zadaniu prymalnym musi być spełnione równościowo”
W naszym przypadku rozwiązujemy układ:
2x1 – 3x2 = 2
2x1 – 2x2 = -2
„jeżeli w którymś z ograniczeń zadania prymalnego zachodzi ´ścisła nierówność w punkcie
optymalnym, to odpowiednia zmienna dualna musi mieć wartość równą zero”
Dla naszego przypadku spełnione są nierówności:
6x1 – 10x2 > 47
2x1 - 3x2 > 13, zatem zerujemy λ1 i λ2, co w konsekwencji daje nam układ równań:
6*0 + 2*0 + 2λ3 + 4λ4 = 6
-10*0 – 3*0 - 2λ3 – 7λ4 = -9
???????
Postać standardowa:
Min x1 + 2x2
3x1 + x2 – x3 = 7
x1 + 4x2 – x4 = 6
x1, x2, x3, x4 >= 0
sztampa z książki, s. 59
Na zmienne bazowe wybieramy x3 i x4 . Zatem xB =[-7;-6] nie spełnia warunku nieujemności
ale ten punkt jest dualnie dopuszczalny ponieważ:
c^ = c – A[AB]-T cB0 = [1;2;0;0] - A[AB]-T * 0 = [1;2;0;0] >= 0.
Początkowa tablica sympleksowa ma postać:
cn
|
1
2
0
0
|-f^
-------------------------------------------------------------x3
|
-3
-1
1
0
|-7
x4
|
-1
-4
0
1
|-6
-----
Jedziemy z iteracją. Mamy inne kryterium stopu teraz: bn^ > 0.
Wyprowadzamy z bazy: x3 (bo -7 < -6)
Szukamy co wprowadzić do bazy: max { (c1 = 2 )/-3 ; (c2 =2)/-1 } = max { -2/3; -1/2 }, czyli
wybieramy x2. Potem z grubsza tak samo:
cn
|
-5
0
-2
0
|-f^
-----------------------------------------------------------------X2
|
3
1
-1
0
|7
x4
|
11
0
4
1
|22
Warunek stopu spełniony. Koniec.