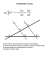Twierdzenie Talesa

ROZDZIAŁ I
Twierdzenie Talesa
1. (Twierdzenie Talesa) Udowodnij, że jeżeli ramiona kąta
przetniemy prostymi równoległymi, to odcinki wyznaczone na jednym ramieniu kąta są proporcjonalne do odpowiednich odcinków na
drugim ramieniu kąta.
2. Ramiona kąta przecięto dwiema prostymi równoległymi jak
na powyższym rysunku. Udowodnij, że
|AC|
|SC|
=
.
|BD|
|SD|
3. (Twierdzenie odwrotne do twierdzenia Talesa)
Udowodnij, że jeżeli ramiona kąta przetniemy dwiema prostymi
i odcinki wyznaczone przez te proste na jednym ramieniu kąta są
proporcjonalne do odpowiednich odcinków na drugim ramieniu kąta,
to proste te są równoległe.
Dokument pochodzi ze strony www.gwo.pl
ROZDZIAŁ VI
Twierdzenie cosinusów
86. (Twierdzenie cosinusów) Udowodnij, że w dowolnym
trójkącie kwadrat długości boku równa się sumie kwadratów długości
pozostałych boków , zmniejszonej o podwojony iloczyn długości tych
boków i cosinusa kąta zawartego między nimi.
√
87.√Oblicz kąty trójkąta
ABC,
w
którym
|BC|
=
2
3, |AC| =
√
= 3 − 3 i |AB| = 3 2.
88. Jakim trójkątem (prostokątnym, ostrokątnym czy rozwartokątnym) jest trójkąt, którego boki mają długości: (a) 2, 3, 4,
(b) 3, 4, 5, (c) 4, 5, 6 ?
)
89. W trójkącie ABC bok BC ma długość 21, <A
= 60◦ oraz
|AC| : |AB| = 3 : 8. Oblicz długości boków AC i AB.
90. W
√ czworokącie wypukłym √ABCD dane są |AB| = 3,
|BC| = 19, |AC| = 5, |CD| = 21 i |AD| = 4. Oblicz długość przekątnej BD.
91. Oblicz długości środkowych trójkąta o danych długościach
boków.
92. Oblicz pole równoległoboku, mając dane długości jego
boków i kąt między przekątnymi.
Dokument pochodzi ze strony www.gwo.pl
ROZWIĄZANIA
ROZDZIAŁ I
1. Przyjmijmy oznaczenia jak na rysunku 1.1.
Udowodnimy dwie równości:
(1)
|SC|
|SA|
=
|CD|
|AB|
oraz
(2)
|SD|
|SB|
=
.
|SC|
|SA|
Rys. 1.1
Zauważmy najpierw, że jeśli dwa trójkąty mają wspólną wysokość, to stosunek ich pól jest równy stosunkowi boków, do których
poprowadzono tę wysokość (dlaczego?). Wobec tego
|SC|
PSCA
=
,
|CD|
PCDA
bo trójkąty SCA i CDA mają wspólną wysokość z wierzchołka A.
Ponadto PCDA = PCBA , gdyż trójkąty te mają wspólny bok
AC i równe wysokości poprowadzone do tego boku. Stąd
|SC|
|SA|
PSCA
=
=
,
|CD|
PCBA
|AB|
Dokument pochodzi ze strony www.gwo.pl
32
ROZWIĄZANIA – ROZDZIAŁ I
bo trójkąty SCA i CBA mają wspólną wysokość poprowadzoną
z wierzchołka C. Udowodniliśmy więc równość (1).
Skorzystamy z niej w dowodzie równości (2):
|SD|
|SC| + |CD|
=
=
|SC|
|SC|
|CD|
|AB|
=1+
=1+
=
|SC|
|SA|
|SA| + |AB|
|SB|
=
=
.
|SA|
|SA|
Łatwe uogólnienie twierdzenia dla przypadku, gdy więcej niż
dwie proste równoległe przecinają ramiona kąta, pozostawiamy
Czytelnikowi.
2. Poprowadźmy prostą CE równoległą do SB (rys. 1.2). Czworokąt ACEB jest równoległobokiem, zatem
|AC|
|BE|
=
.
|BD|
|BD|
Z twierdzenia Talesa (dla kąta o wierzchołku D o ramionach przeciętych prostymi równoległymi CE i SB ) mamy równość
|BE|
|SC|
=
.
|BD|
|SD|
Zatem
|AC|
|SC|
=
.
|BD|
|SD|
Rys. 1.2
Rys. 1.3
Dokument pochodzi ze strony www.gwo.pl