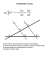Twierdzenie Talesa - BEZ

Twierdzenie Talesa Jeżeli ramiona kąta przetniemy dwiema
prostymi równoległymi, to długości odcinków wyznaczone przez
te proste na jednym ramieniu kąta są proporcjonalne do
długości odpowiednich odcinków wyznaczonych przez te proste
na drugim ramieniu kąta. Twierdzenie odwrotne do
twierdzenia Talesa. Jeśli odcinki wyznaczone przez dwie
proste na jednym ramieniu kąta są proporcjonalne do
odpowiednich odcinków wyznaczonych przez te proste na
drugim ramieniu kąta, to proste te są równoległe Twierdzenie o
dwusiecznej kąta- Oznaczamy trójkąt ABC i jego boki a, b, c
tak aby bok a leżał naprzeciwko wierzchołka A. W trójkącie
rysujemy dwusieczną kąta A. Dzieli ona nam odcinek a na dwie
części x, y x-odcinek o początku przy wierzchołku B i końcu
przy dwusiecznej y-odcinek o początku przy wierzchołku C i
końcu przy dwusiecznej Podobieństwo – przekształcenie
geometryczne zachowujące stosunek odległości punktów.
Także relacja równoważności utożsamiająca figury
geometryczne, które nazywane są wtedy podobnymi, o ile
istnieje podobieństwo przeprowadzające jedną na drugą.
Własności: Złożenie podobieństw o skalach k1,k2 jest
podobieństwem o skali k1k2 Dowolne podobieństwo
trójwymiarowej przestrzeni euklidesowej jest złożeniem
izometrii i jednokładności o skali równej skali podobieństwa.
▪ Podobieństwo jest izometrią wtedy i tylko wtedy, gdy k = 1
Z definicji oraz powyższych własności wynika, że w figurach
podobnych w przestrzeniach euklidesowych: ▪ stosunek
długości odpowiadających sobie odcinków jest równy skali
podobieństwa; ▪ odpowiadające sobie kąty są przystające; ▪
stosunek pól figur płaskich jest równy kwadratowi skali
podobieństwa, ▪ stosunek objętości figur przestrzennych jest
równy sześcianowi skali podobieństwa Przystawanie – cecha
figur geometrycznych intuicyjnie rozumiana jako identyczność
kształtu i wielkości. Dwie figury uważa się za przystające, jeśli
istnieje izometria całej przestrzeni przekształcająca jedną figurę
na drugą. Ponieważ każdą izometrię można rozłożyć na obroty
i translacje, i ewentualnie symetrię, więc daje to wygodne
kryterium rozpoznawania figur przystających: ,, Figury A i B są
przystające, jeśli figurę B można otrzymać z figury A za
pomocą skończonej liczby obrotów, przesunięć i symetrii.”
Trójkąty podobne to każda para trójkątów, których kąty są
odpowiednio równe, a boki odpowiednio proporcjonalne.
Twierdzenia o podobieństwie trójkątów (cechy podobieństwa):
Cecha bbb (bok-bok-bok) - jeśli stosunki długości odpowiednich
par boków są równe, to trójkąty są podobne. Cecha bkb (bokkąt-bok) - jeśli stosunki długości dwóch boków i miary kątów
między tymi bokami są równe, to trójkąty są podobne Cecha kk
(kąt-kąt): - jeśli dwa kąty jednego trójkata są równe
odpowiednim dwóm kątom drugiego trójkąta, to są to trójkąty
podobne (bo ostatnia para kątów też musi być równa, aby
suma ich miar była równa 180°). Jeśli trójkąty są podobne, to: ▪
wszystkie szczególne odcinki jednego trójkąta (wysokości,
środkowe, odcinki dwusiecznych, promienie kół: opisanego i
wpisanego itp.) są proporcjonalne do odpowiednich odcinków
drugiego trójkąta w tej samej skali s. ▪ stosunek ich pól jest
równy kwadratowi skali podobieństwa.
bez-nauki.pl - ściągi, opracowania, testy...