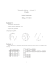[ ] 1

Spis treści
Podstawowe pojęcia
Drogi Eulera
Grafy dwudzielne. Skojarzenia
Przykłady
O szukaniu drogi do celu oraz dobrej partii
Twierdzenia Eulera i Halla
Matematyczny czwartek na UJ
Leszek Pieniążek
http://www.im.uj.edu.pl/LeszekPieniazek
9 stycznia 2014
Literatura
Spis treści
Podstawowe pojęcia
Drogi Eulera
Podstawowe pojęcia
Definicje
Drogi Eulera
Sformułowanie problemu i dowód
Grafy dwudzielne. Skojarzenia
Twierdzenie Halla i jego dowody
Przykłady
Zastosowanie twierdzenia Halla
Literatura
Grafy dwudzielne. Skojarzenia
Przykłady
Literatura
Spis treści
Podstawowe pojęcia
Drogi Eulera
Grafy dwudzielne. Skojarzenia
Przykłady
Literatura
Definicja 1.1
Grafem nazywać będziemy parę G = (V , E ), gdzie V jest zbiorem
skończonym, zaś E skończonym zbiorem krawędzi.
Rozważać będziemy tu wyłącznie grafy nieskierowane, w których nie
wyróżniamy początku i końca krawędzi. Pętlą nazywamy krawędź łączącą
wierzchołek z samym sobą.
Uwaga
Może być wiele krawędzi łączących te same wierzchołki. Najczęściej
wizualizujemy grafy jako zbiór obiektów na płaszczyźnie reprezentujących
wierzchołki oraz linie je łączące obrazujące krawędzie.
f
1
g
e
2
a
3
d
4
h
b
c
5
Spis treści
Podstawowe pojęcia
Drogi Eulera
Grafy dwudzielne. Skojarzenia
Przykłady
Literatura
Definicja 1.2
Drogą lub ścieżką w grafie G nazywamy taki ciąg wierzchołków
v1 , v2 , . . . , vn+1 ∈ V (G ) oraz takich krawędzi e1 , e2 , . . . , en ∈ E (G ), że
każda z krawędzi ei łączy wierzchołki vi z vi+1 . Mówimy wtedy, że droga
łączy wierzchołki v1 i vn+1 zaś n nazywamy długością drogi.
Drogę łączącą v1 i vn+1 nazywamy zamkniętą, jeśli v1 = vn+1 .
Graf nieskierowany nazywamy spójnym, jeśli istnieją drogi łączące każde
dwa jego różne wierzchołki.
f
Przykład 1.1
1
g
e
2
a
3
d
4
h
b
c
5
Pierwszy graf powyżej jest niespójny. Drugi, którego wierzchołki
i krawędzie zostały opisane liczbami i literami, jest spójny.
Przykładem drogi zamkniętej jest (1, 2, 3, 4, 1) oraz (a, f , g , b).
Spis treści
Podstawowe pojęcia
Drogi Eulera
Grafy dwudzielne. Skojarzenia
Przykłady
Literatura
Definicja 2.1
Stopniem wierzchołka v ∈ V (G ) grafu nazywamy deg(v ), liczbę
krawędzi o końcu w v , przy czym pętle liczymy dwukrotnie. Drogą
(cyklem) Eulera w grafie nieskierowanym G nazywamy taką drogę
(zamkniętą), która zawiera wszystkie krawędzie z E (G ) dokładnie raz.
Lemat 2.1
Suma stopni wszystkich wierzchołków równa jest podwojonej liczbie
wszystkich krawędzi grafu.
Przykład 2.1
Graf po lewej z poprzedniej strony ma wierzchołek najwyższego stopnia
6. Nie ma drogi Eulera ze względu na niespójność. Graf koperta ma jeden
wierzchołek stopnia 2 oraz po 2 stopnia 3 i 4. Istnieje w nim cykl Eulera:
(1, 2, 3, 4, 5, 1, 4, 2, 5) (pomijamy krawędzie).
Przykład 2.2 (Mosty Królewca)
Mapa Królewca
(http://it.wikipedia.org/wiki/File:Koenigsberg,_Map_by_Bering_1613.jpg)
Sformułowanie problemu
(http://pl.wikipedia.org/wiki/Zagadnienie_mostów_królewieckich)
Spis treści
Podstawowe pojęcia
Drogi Eulera
Grafy dwudzielne. Skojarzenia
Przykłady
Literatura
Spis treści
Podstawowe pojęcia
Drogi Eulera
Grafy dwudzielne. Skojarzenia
Przykłady
Literatura
Twierdzenie 2.2
Graf ma cykl Eulera wtedy i tylko wtedy, gdy jest spójny i ma każdy
wierzchołek stopnia parzystego. Taki graf nazywamy grafem
eulerowskim.
Graf ma drogę Eulera wtedy i tylko wtedy, gdy jest spójny i ma nie więcej
niż 2 wierzchołki stopnia nieparzystego. Takie grafy nazywane bywają
grafami jednokreślnymi.
e
2
a
Przykład 2.3
1
d
3
f
b
c
4
Problem mostów królewieckich ilustruje pierwszy graf powyżej o 4
wierzchołkach i 7 krawędziach. Nie istnieje w nim droga Eulera, bo każdy
z wierzchołków ma nieparzysty stopień. Zamknięta koperta obok jest
jednym z najprostszych grafów niejednokreślnych. Pierwszy z grafów
z Przykładu 1.1 spełnia założenia o stopniu wierzchołków z powyższego
twierdzenia, ale ze względu na niespójność nie istnieje w nim droga
Eulera.
Spis treści
Podstawowe pojęcia
Drogi Eulera
Grafy dwudzielne. Skojarzenia
Przykłady
Literatura
Twierdzenie 2.3
Drogę Eulera w grafie spełniającym założenia poprzedniego twierdzenie można
znaleźć korzystając z poniższego Algorytmu Fleury’ego.
(A) Wybieramy v dowolny wierzchołek stopnia nieparzystego, jeśli istnieje taki,
lub dowolny, jeśli wszystkie mają stopień parzysty; v0 := v dodajemy do
drogi.
(B) Jeśli G nie ma krawędzi to procedura zakończona.
(C) Jeśli z v0 wychodzi wiele krawędzi wybieramy taką krawędź e łączącą v0
z pewnym w , aby po usunięciu jej graf pozostał spójny; dodajemy w oraz
e do drogi i usuwamy e z grafu G .
v0 := w . Powrót do (B).
(D) Jeśli z v0 wychodzi jedna krawędź e łącząca v0 z jakimś w , dodajemy w
oraz e do drogi usuwając równocześnie v0 i e z grafu G .
v0 := w . Powrót do (B).
Poprawność algorytmu wynika z następujących faktów:
1. Każdy powrót do (B) oznacza zmniejszenie liczby krawędzi grafu G o 1, a więc algorytm
zatrzyma się.
2. W (B) po każdym kroku liczba wierzchołków o nieparzystym stopniu jest równa 0 lub 2.
Przy tym w tej drugiej sytuacji v0 jest jednym z nich.
3. W (C) usunięcie co najwyżej jednej krawędzi rozspójnia graf.
4. W (B) po każdym kroku graf jest spójny.
Spis treści
Podstawowe pojęcia
Drogi Eulera
Grafy dwudzielne. Skojarzenia
Przykłady
Literatura
Definicja 3.1
Graf G = (V , E ) nazywamy dwudzielnym, jeśli istnieją rozłączne zbiory
V1 , V2 takie, że V = V1 ∪ V2 oraz jeśli e ∈ E łączy v i w , to należą one
do różnych zbiorów Vi .
Uwaga
W grafie dwudzielnym podział V (G ) na podzbiory jest jednoznaczny
wtedy i tylko wtedy, gdy graf jest spójny.
Lemat 3.1
Graf jest dwudzielny wtedy i tylko wtedy, gdy każdy cykl (zamknięta
droga, w której nie powtarzają się wierzchołki) w nim ma parzystą
długość.
Przykład 3.1
Poniższy rysunek przedstawia graf, w którym są cykle wyłącznie długości
2 i 4.
c
c
2 V2
2
3
V1 3 e d
a
1
d
b
e
4
a
1
b
4
Spis treści
Podstawowe pojęcia
Drogi Eulera
Grafy dwudzielne. Skojarzenia
Przykłady
Literatura
Definicja 3.2
Skojarzeniem w grafie dwudzielnym (V1 ∪ V2 , E ) nazywamy dowolny
zbiór jego krawędzi F ⊂ E , które nie łączą tych samych wierzchołków.
Pełnym skojarzeniem V1 z V2 nazywamy skojarzenie, w którym
z każdego wierzchołka V1 wychodzi krawędź.
Dla W ⊂ V1 oznaczmy przez ΦE (W ) zbiór wierzchołków z V2
połączonych w grafie z wierzchołkami z W . Formalnie,
ΦE (W ) = {v ∈ V2 : ∃w ∈ W : wv ∈ E }.
Przykład 3.2
W Przykładzie 3.1 pełnymi skojarzeniami są {a, e}, {b, c}, {b, d }. Jest
też ΦE (∅)=∅, ΦE ({1})={2, 4}, ΦE ({3})={2, 4}, ΦE ({1, 3})={2, 4}.
Twierdzenie 3.2 (P. Hall 1935)
Niech G = (V1 ∪ V2 , E ) będzie grafem dwudzielnym. Wówczas pełne
skojarzenie V1 z V2 istnieje wtedy i tylko wtedy, gdy |W | 6 |ΦE (W )| dla
każdego podzbioru W ⊂ V1 .
Spis treści
Podstawowe pojęcia
Drogi Eulera
Grafy dwudzielne. Skojarzenia
Przykłady
Literatura
Uwaga
Warunek |W | 6 |ΦE (W )| dla każdego podzbioru W ⊂ V1 nazywać
będziemy warunkiem małżeńskim (WM). Istnienie pełnego skojarzenia
w oczywisty sposób implikuje warunek małżeński. Będziemy jedynie
pokazywać, że jest to również warunek wystarczający dla istnienia
pełnego skojarzenia.
Dowód 1.
• Jeśli V1 = {v } jest jednoelementowy, (WM) implikuje istnienie co najmniej
jednej krawędzi e ∈ E . {e} jest szukanym dopasowaniem.
• Jeśli dla każdego niepustego zbioru W
V1 jest |W | < |ΦE (W )| kojarzymy
dowolny element v1 ∈ V1 z pewnym dozwolonym v2 ∈ V2 , a następnie
procedurę stosujemy do grafu G 0 = (V1 \ {v1 } ∪ V2 \ {v2 }, E 0 ), gdzie E 0
składa się z tych krawędzi z E , które nie łączą żadnego z wierzchołków v1 , v2 .
V1
V2 V1
V1
V2
V2
Spis treści
Podstawowe pojęcia
Drogi Eulera
Grafy dwudzielne. Skojarzenia
Przykłady
• Jeśli dla pewnego niepustego W V1 zachodzi |W | = |ΦE (W )|
osobno poszukamy skojarzeń dla zbiorów W ∪ ΦE (W ) oraz
(V1 \ W ) ∪ (V2 \ ΦE (W )).
V1
V2 V1
V2
W
(WM) dla W ∪ ΦE (W ) jest oczywisty, istnieje więc pełne skojarzenie.
Jeśli Z ⊂ (V1 \ W ) to |Z | + |W | = |Z ∪ W | 6 |ΦE (Z ∪ W )| =
|ΦE (Z ) ∪ ΦE (W )| 6 |ΦE (Z )| + |ΦE (W )| = |ΦE (Z )| + |W |, a więc
spełniony jest (WM) dla (V1 \ W ) ∪ (V2 \ ΦE (W )).
Literatura
Spis treści
Podstawowe pojęcia
Drogi Eulera
Grafy dwudzielne. Skojarzenia
Przykłady
Literatura
Dowód 2.
Graf dwudzielny (V1 ∪ V2 , E ) można opisać jako macierz (tablicę liczb)
mającą tyle kolumn, ile elementów ma V1 oraz tyle wierszy, ile elementów
ma V2 . Każdą kolumnę utożsamiamy z jednym z elementów V1 zaś
wiersz z elementem V2 . Jeśli w grafie istnieje krawędź łącząca v1 ∈ V1
z v2 ∈ V2 , to w przecięciu kolumny odpowiadającej v1 i wiersza
odpowiadającego v2 wpisujemy 1, w przeciwnym razie 0. Wyraz macierzy
w i-tym wierszu i j-tej kolumnie będziemy oznaczać przez aij . Przekątną
macierzy nazwiemy wyrazy aii dla wszystkich dopuszczalnych i.
Zauważmy, że zamiana miejscami kolumn lub wierszy daje macierz
opisującą ten sam graf ze zmienionym przyporządkowaniem wierzchołków
do wierszy i kolumn. Ponadto pełne skojarzenie oznacza, że przy pewnym
przypisaniu wierzchołkom kolumn i wierszy wyrazy aii = 1 dla wszystkich
dopuszczalnych i. Pokażemy więc, że jeśli spełniony jest (WM), to można
tak przemieszać wiersze i kolumny, aby na przekątnej nie było zer.
Spis treści
Podstawowe pojęcia
Drogi Eulera
Grafy dwudzielne. Skojarzenia
Przykłady
Przykład 3.3
Przykładowo, dla grafu ze strony 12, w którym numerujemy kolejno
wierzchołki w zbiorach z góry na dół, otrzymujemy macierz A1 , zaś po
zamianie 2 pierwszych wierszy macierz A2 mającą na przekątnej
wyłącznie jedynki.




1 1 1 0
1 0 0 1
1 0 0 1
1 1 1 0





0 1 1 0
0
1
1
0
A1 = 
A
=
2




0 0 0 1
0 0 0 1
0 0 0 1
0 0 0 1
Oznacza to, że pełnym (choć nie jedynym możliwym) skojarzeniem jest
1 → 2, 2 → 1, 3 → 3, 4 → 4.
Literatura
Spis treści
Podstawowe pojęcia
Drogi Eulera
Grafy dwudzielne. Skojarzenia
Przykłady
Literatura
Lemat 3.3
Jeśli aii = 1 dla i < m, amm = 0 oraz ajk = 1 dla pewnych j, k > m to
zamiana miejscami kolumn o numerach m, k oraz wierszy o numerach
m, j daje amm = 1.
Lemat 3.4
Jeśli aii = 1 dla i < m, ajk = akl = 1 dla pewnego k < m oraz j, l > m,
to zamiana miejscami kolumn k, m, a następnie procedury z lematu 3.3,
dają aii = 1 dla i 6 m.
[ ][ ] [ ][ ]
...
...
...
(k)
1
(j)
1
0
1
1
...
(k)
1
(k)
(m)
(k)
Lemat 3.5
Jeśli aii = ajj to zamiana miejscami kolumn i, j oraz wierszy i, j nie
zmienia liczby i położenia jedynek na przekątnej.
(k)
...
(m)
1
...
(k)
(j)
...
(m)
... 0 ...
1
0
1
...
(j)
(m)
1
... ...
1
...
... 1 ...
(m)
1
...
...
1
0
1
1
...
1
(m)
(j)
Spis treści
Podstawowe pojęcia
Drogi Eulera
Grafy dwudzielne. Skojarzenia
Przykłady
Algorytm McWortera.
1. Używając Lematu 3.3 doprowadzamy do postaci aii = 1 dla i 6 m oraz
ajk = 0 gdy j, k > m. (Rys. 1)
2. Używając Lematów 3.4 i 3.5 doprowadzamy do sytuacji jak na Rys. 2.
W każdej z kolumn E1 jest co najmniej jedna 1. Gdyby E1 było puste lub
G1 zawierałoby wyrazy wyłącznie zerowe, (WM) nie byłby spełniony i nie
istniałoby pełne skojarzenie.
3. Jeśli ajk = 1 leży w F1 oraz akl = 1 leży w G1 , zamiana kolumn k, l
powoduje, że spełnione są założenia Lematu 3.4, więc można zwiększyć
liczbę jedynek na przekątnej. (Rys. 3). Powracamy do punktu 2.
4. Zamieniając parami wiersze i kolumny jak w Lemacie 3.5, doprowadzamy
macierz do postaci jak na Rys. 4. Powtarzamy procedurę z punktu 3. dla
macierzy F2 i G2 i dalej, dopóki w odpowiednich blokach nie otrzymamy
konfiguracji pozwalającej zwiększyć liczby jedynek na przekątnej, lub nie
dostaniemy sprzeczności z (WM).
[ ][ ][ ][ ]
Rys. 2
1
F1
1
1
0 E1
(k)
1
G2
0
0 E2 1 1 0
0 E1 0
G1
0
0
Rys. 3
1
F2
1
1
...
0
1
...
1
0 E1
G1
0
...
Rys. 1
F1
1
...
0
1
...
F0
1
...
...
1
G0
...
...
1
(l)
Rys. 4
Literatura
Spis treści
Podstawowe pojęcia
Drogi Eulera
Grafy dwudzielne. Skojarzenia
Przykłady
Literatura
Twierdzenie 3.6
Powyższy algorytm pozwala sprawdzić spełnianie warunku małżeńskiego
oraz znaleźć pełne skojarzenie, jeśli istnieje. Procedura z punktu 4. nie
może iterować się w nieskończoność, ze względu na malenie szerokości
macierzy Fi w każdej iteracji.
Spis treści
Podstawowe pojęcia
Drogi Eulera
Grafy dwudzielne. Skojarzenia
Przykłady
Literatura
Przykład 4.1
Rozszerzenie twierdzenia Halla dostaniemy, jeśli zażądamy, aby każdy
z elementów v ∈ V1 miał przypisaną pewną dodatnią liczbę kv skojarzeń
z elementami zbioru V2 . Koniecznym i wystarczającym warunkiem
zapewniającym, że to się da zrobić, jest, aby dla dowolnego W ⊂ V1
suma wartości
P kv dla wszystkich v ∈ W była nie większa niż |ΦE (W )|.
(Formalnie: v ∈W kv 6 |ΦE (W )|.)
Każdy z wierzchołków v ∈ V1 zastępujemy jego kv kopiami
z krawędziami prowadzącymi do tych samych wierzchołków z V2 .
Przykład 4.2
Mamy daną macierz n × n wypełnioną 0 i 1 tak, że aij = 0 ⇐⇒ 2|i + j.
Czy można zamieniając miejscami kolumny i wiersze przekształcić ją do
postaci, w której przekątna wypełniona jest jedynkami?
Jeśli n jest parzyste, łatwo uzyskać szukany układ zamieniając kolumny
o numerach 2k i 2k + 1 parami.
Dla n nieparzystego nie da się tego zrobić, bo graf reprezentowany przez
daną macierz nie spełnia warunku (WM) dla zbioru W wierzchołków
odpowiadających kolumnom nieparzystym i ΦE (W ) będącym zbiorem
wierzchołków odpowiadających wierszom parzystym.
Spis treści
Podstawowe pojęcia
Drogi Eulera
Grafy dwudzielne. Skojarzenia
Przykłady
Literatura
Przykład 4.3
Prostokątem łacińskim nazywamy macierz m × n wypełnioną liczbami
naturalnymi od 1 do max{m, n} w ten sposób, że w żadnym wierszu
i żadnej kolumnie nie powtarza się żadna z liczb. Można uzasadnić, że
każdy prostokąt łaciński niebędący kwadratem można powiększyć do
kwadratu łacińskiego przez dopisanie nowych wierszy lub kolumn.
Możemy przyjąć, że prostokąt ma więcej kolumn niż wierszy. Niech V1
składa się z n kolumn macierzy zaś V2 z liczb {1, 2, . . . , n}. Prowadzimy
krawędzie pomiędzy każdą z kolumn a liczbami, które nie znajdują się w
niej. Z każdego wierzchołka V1 wychodzi dokładnie n − m krawędzi i do
każdego wierzchołka V2 dochodzi n − m krawędzi. Zatem w każdy zbiór
k kolumn musi być połączony z co najmniej k liczbami.
Przykład 4.4
Talię 52 kart dzielimy na 13 kupek po 4 karty. Można wybrać wtedy po
jednej karcie z każdej kupki w ten sposób, że każda z kart jest inna.
Spis treści
Podstawowe pojęcia
Drogi Eulera
Grafy dwudzielne. Skojarzenia
Literatura
1. Cut the knot, http://www.cut-the-knot.org/
2. Wikipedia, http://en.wikipedia.org/
3. Wikipedia, http://pl.wikipedia.org/
Przykłady
Literatura