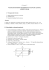74. Pokaż, korzystając z tabeli pochodnych funkcji

WM-E; kier. MBM, lista zad. nr 11 pt. (z karty przedmiotu): Analiza i rozwiązywania zadań z zakresu dynamiki ruchu
drgającego: harmonicznego prostego, tłumionego, wymuszonego i rezonansu mechanicznego. Rozwiązywanie zadań
z zakresu fizyki fal mechanicznych i akustycznych i obliczanie wartości podstawowych wielkości ruchu falowego. Lista ma na
celu zdobycie przez studentów wiedzy matematyczno-fizycznej, nabycie umiejętności rozwiązywania prostych zadań
dotyczących dynamiki ruchów drgających, ruchu falowego i utrwalanie dotychczas zdobytej wiedzy fizycznej.
74. Pokaż, korzystając z tabeli pochodnych funkcji trygonometrycznych, że rozwiązaniami równanie
2
ruchu drgań harmonicznych prostych d x (2 t ) = ɺɺx (t ) = −ω02 ⋅ x ( t ) są funkcje: a) x ( t ) = x0 sin (ω0t + ϕ 0 ) , b)
dt
x ( t ) = x1 cos (ω0t + α1 ) , gdzie x0 , ϕ 0 , x1 , α1 są parametrami wyznaczanymi z warunków początkowych.
Przyjmując za rozwiązanie funkcję podaną w a) wyznacz wartości parametrów x0 , ϕ 0 , jeśli w chwili
początkowej t0=0 mamy x ( t0 ) = A i v (t0 ) = dx ( t )
dt
= V0 .
t = t0
75. Ciało o masie 10 kg wykonuje drgania harmoniczne proste opisane wzorem x(t) = 0,06·cos[3πt +
π/3] (użyto jednostki SI). Ile wynosi okres i częstość drgań? Dla chwili t = 2 s wyznaczyć:
przemieszczenie, prędkość, przyspieszenie, energię drgań, fazę i siłę przyłożoną do ciała.
76. Masa m jest przyczepiona do dwóch sprężyn o stałych sprężystości
k1 i k2 (patrz rys. obok). W obu przypadkach zostaje ona wychylona z
położenia równowagi i puszczona; porusza się bez tarcia. Pokazać, że
wykonuje ona ruch harmoniczny prosty o okresach odpowiednio
TA = 2π
m ( k1 + k2 )
i TB = 2π m .
k1k2
k1 + k2
77. Wyprowadź wzór na okres drgań wahadła fizycznego, korzystając z II
zasady dynamiki dla ruchu obrotowego bryły sztywnej.
78. Jednorodną kulę o masie M i promieniu R
podwieszono w punkcie Pivot odległym o d od jej
środka masy, co przedstawia rysunek obok po prawej
stronie. Wyznacz częstotliwość małych drgań kuli
wychylonej z położenia równowagi. Rozwiąż to samo
zagadnienie dla jednorodnego pręt o masie M i dł. L podwieszonego w punkcie
O, jak przedstawia to rysunek obok po lewej stronie.
79. Układ złożony z dwóch klocków (m = 1 kg i M = 10 kg; lżejszy klocek
spoczywa na cięższym) i sprężyny (k = 300N/m) ustawiono na poziomej
idealnie gładkiej powierzchni. Współczynnik tarcia statycznego między
klockami wynosi 0,4. Dla jakich amplitud ruchu harmonicznego układu
mniejszy klocek pozostanie nieruchomy? Ws-ka: Jaką wartość ma maksymalne przyspieszenie w tym
ruchu?
80. Na doskonale gładkim stole leży klocek o masie 1 kg. Klocek
przymocowany jest do ściany za pomocą sprężyny o współczynniku
sprężystości k=500 N/m (patrz rysunek po lewej stronie) i zaniedbywalnie
małej masie. W klocek ten uderza lecący poziomo pocisk i grzęźnie w nim.
Prędkość pocisku przed zderzeniem wynosi 50 m/s, a jego masa 0,1 kg. Po zderzeniu klocek wraz z
uwięzionym w nim pociskiem wykonuje drgania harmoniczne. Jaka jest energia całkowita tych drgań?
O ile zostanie ściśnięta sprężyna? Jaka będzie amplituda i częstotliwość drgań?
W. Salejda
Wrocław, 30 listopada 2015
1
Siłownia umysłowa. Zadania przeznaczone do samodzielnego rozwiązania
1. Ciężarek o masie m przymocowany do poziomej sprężyny wykonuje ruch drgający harmoniczny
poruszając się po idealnie gładkiej poziomej powierzchni. W czasie t pokonuje drogę d między skrajnymi
wychyleniami z położenia równowagi. Ile wynosi energia mechaniczna tych drgań?
2. Klocek o masie 0,25 kg przymocowany do sprężyny wykonuje na doskonale gładkim stole drgania
harmoniczne o energii całkowitej równej 50 J. Wyznacz wartość energii kinetycznej tego klocka w
momencie, gdy jego wychylenie liczone od punktu równowagi jest równe połowie wartości amplitudy
drgań.
3. Przy jakiej prędkości samochód poruszający się po drodze z betonowych płyt będzie silnie drgał w
kierunku pionowym, jeśli długość płyty wynosi L, a nacisk na resor, który ugina się o ∆x pod działaniem
siły Fx, wynosi N1?
4. Ile wynosi okres drgań wahadła matematycznego: a) W windzie jadącej w górę z przyspieszeniem a?
b) W windzie jadącej w dół z przyspieszeniem a? c) Wiszącego w wózku zsuwającym się bez tarcia po
równi pochyłej o kącie nachylenia α? Ws-ka do pkt. c) Pokaż, że w tym układzie wypadkowe
przyspieszenie „grawitacyjne” wynosi a = g 2 − ( g sin α ) = g cos α .
2
5. Dwa jednorodne pręty o masach M i dł. L, połączono w kształcie litery T i
podwieszono w punkcie A, co przedstawia rysunek obok po prawej stronie. Wyznacz
okres małych drgań układu wychylonego z położenia równowagi. Ws-ka. Należy
najpierw wyznaczyć odległość d środka masy układu od punktu A, następnie moment
bezwładności J całego układu względem punktu A i na końcu policzyć okres ze wzoru
dla wahadła fizycznego T = 2π ( J mgd ) . Patrz także zadanie rozwiązane poniżej pt.
1/2
Podwójny Steiner.
6. Do końców jednorodnego pręta o dł. L i masie M przytwierdzone są
punktowe masy m1 i m2, co pokazuje rysunek po lewej stronie. Wyznacz
częstotliwość małych drgań układu wychylonego z położenia równowagi. Wska. Należy najpierw wyznaczyć odległość d środka masy układu od osi obrotu,
następnie moment bezwładności J całego układu względem tej osi i na końcu
częstotliwość. Patrz także zadanie rozwiązane poniżej pt. Podwójny Steiner.
7. Układ mechaniczny tworzą połączone ze sobą jednorodny pręt o dł. L i masie M oraz jednorodna kulka o
masie m i promieniu r, co ilustruje rysunek po prawej
stronie. Wyznacz okres małych drgań układu wychylonego z położenia równowagi. Ws-ka. Należy najpierw wyznaczyć odległość d środka masy układu od osi
obrotu, następnie moment bezwładności J całego układu względem tej osi i na
końcu policzyć okres ze wzoru dla wahadła fizycznego T = 2π ( J mgd ) . Patrz
1/2
także zadanie rozwiązane poniżej pt. Podwójny Steiner.
8. Podwójny Steiner. Kwadratową ramkę podwieszono jak na rysunku obok. Masa
każdego boku o dł. L wynosi m. Wyznacz częstotliwość małych drgań ramki wokół
punktu zawieszenia.
Rozwiązanie
Układ potraktujemy jako wahadło fizyczne, którego środek o masie 4m znajduje
się od punktu podwieszenia w odległości d = L 2 2. Częstotliwość drgań
wyznaczamy ze wzoru υ = 2π 4mgd J gdzie J jest momentem bezwładności ramki względem punktu
zawieszenia. Aby określić jego wartość skorzystamy dwukrotnie z tw. Steinera, na podstawie którego
2
(
)
2
(względem punktu zawieszenia Hook) J = J 0 + 4md 2 = J 0 + 4m L 2 2 = J 0 + 2mL2 , gdzie J0 oznacza
nieznany moment bezwładności ramki wg. jej środka masy. Teraz po raz drugi wykorzystamy tw.
Steinera do wyznaczenia momentu bezwładności dowolnego boku ramki wg. środka masy ramki. W tym
celu rozważmy jeden z boków, np. prawy górny bok ramki. Wyobraźmy sobie dwie równoległe osie
prostopadłe do płaszczyzny rysunku, z których jedna przechodzi przez środek masy tego boku, a druga
przez środek masy ramki. Dzieli je odległość d01 = L/2. Na mocy tw. Steinera moment bezwładności J1
tego boku wg. środka masy ramki jest równy J 1 = J 01 + md 012 = J 01 + m ( L 2 ) = J 01 + mL2 4, gdzie J01 jest
2
momentem bezwładności boku ramki, tj. pręta wg. osi przechodzącej przez jego środek, który wynosi
J 01 = mL2 12. Zatem J 01 = mL2 12 + mL2 4 = mL2 3. Całkowity moment bezwładności wszystkich boków
ramki, czyli prętów wg. środka masy ramki wyraża się wzorem J 0 = 4mL2 3. Ostatecznie otrzymujemy
 6⋅ 2  g
 1
4mgd
6⋅ 2 ⋅ g

= 2π
= 2π 
= 0,921
 10  L
J
10 L
 2π


kolejno J = 4mL2 3 + 2mL2 = 10mL2 3 i υ = 2π
g
.
L
9. Sprawdzić, że przy słabym tłumieniu, gdy wartość siły tłumienia F = −bv = −bxɺ , rozwiązaniem
równania ruchu tłumionego ɺɺx + 2 β xɺ + ω02 x ( t ) = 0 ( ɺxɺ oznacza przyspieszenie, tj. drugą pochodną położenia
po czasie) jest funkcja x ( t ) = A exp( − β t )cos (ω ' t − ϕ ) , gdzie ω ' = ω02 − β 2 , 2 β = b / m, ω02 = k / m.
10.
Sprawdzić, że rozwiązaniem równania ruchu wymuszonego
ɺɺ
x + 2 β xɺ + ω02 x ( t ) = f 0 cos (ωt ) m jest
2
funkcja x ( t ) = A cos (ωt − ϕ ) , gdzie A = f 0 m (ω02 − ω 2 ) + 4 β 2ω 2  , tgϕ = 2 βω (ω02 − ω 2 ) . Pokaż, że


wartość częstości rezonansowej wynosi ωrez. = ω02 − 2 β 2 .
11. Ciało o masie 0,8 kg jest podwieszono do pionowej sprężyny z k = 42 N/m i zanurzone w cieczy,
która działa na ciało siłą oporu F = −bv = −bxɺ , gdzie b = 0,7 N·s/m. Wyznacz okres drgań tłumionych. Ile
wynosi logarytmiczny dekrement dla tego ruchu? Podaj zależność położenia od czasu x(t), jeśli dla t = 0,
x = 0, a dla t = 1 s, x = 0,12 m. Ws-ka: Przyjąć rozwiązanie w postaci x ( t ) = A exp( − β t )cos (ω ' t − ϕ ) , gdzie
ω ' = ω02 − β 2 , .
12. Rysunek obok przedstawia początkowe położenie wahadła fizycznego, którym jest
jednorodny pręt o masie 0,20 kg. Drgania pręta są tłumione na skutek tarcia w punkcie
podwieszenia, a siła oporów jest proporcjonalna do dθ/dt. Po 8 s od momentu swobodnego
puszczenia amplituda zmalało do wartości 5,5o. Jeśli przyjąć, że x ( t ) = A exp(− β t )cos (ω ' t ) ,
gdzie ω ' = ω02 − β 2 , , to jaka jest wartość parametru β? Jaki jest okres drgań?
13. Wyznacz częstotliwość małych drgań pręta o masie 2m i długości 2L
zgiętego w połowie długości pod kątem prostym i podpartego na ostrzu, jak na
rysunku obok. Ws-ka. Należy najpierw wyznaczyć odległość d środka masy
układu od punktu zgięcia, następnie moment bezwładności J całego układu
względem tego punktu i na końcu policzyć częstotliwość korzystając ze wzoru
T = 2π ( J mgd ) . Patrz także zadanie pt. Podwójny Steiner.
1/2
3
14. Rysunki poniżej przedstawiają tunele wewnątrz jednorodnej planety o masie M i promieniu R.
Pokazać, że równanie ruchu dla ciała o masie m0 w tunelu ma postać równania oscylatora harmonicznego
d2 x ( t )
g
= ɺɺ
x (t ) = x ( t ) ,
dt 2
R
gdzie g — przyspieszenie grawitacyjne na powierzchni planety, a x oznacza odległość
wskazaną na rysunkach. Oszacować okres oscylacji dla ciała w tunelu we wnętrzu Ziemi i porównać go z
okresem obiegu Ziemi przez satelitę na niskiej orbicie.
Szkic rozwiązania.
Na ciało znajdujące się w odległości x (patrz rysunek) działa siła grawitacyjna pochodząca od masy m(r)
zgromadzona w kuli o promieniu r (patrz rysunek). Wartość tej siły wynosi F(x) = G m0 m(r) /r2 i jest
skierowana do środka Ziemi. Na kierunek tunelu działa siła F(x)·x/r . Ponieważ m(r) = (4/3)πr3
M/[(4/3)πR3], więc m(r) = r3 ·M/R3 i wartość siły F(x)·x/r = (G m0 /r2)· r3 ·M/R3 = (G·M/R3)·r =
m0·g·r/R, gdzie g = G·M/R2 – natężenie pola grawitacyjnego planety (przyspieszenie na powierzchni
planety). Zatem równanie ruchu przyjmuje postać m0
ω0 = (g/R)1/2 i okres drgań wynosi T = 2π
d2 x (t )
g
= m0 ɺɺ
x (t ) = m0 x ( t ) , z którego wynika, że
2
dt
R
R
.
g
W. Salejda
Wrocław, 30 listopada 2015
4