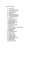S(k+1)

MATEMATYKA DYSKRETNA (2014/2015)
dr hab. inż. Małgorzata Sterna
[email protected]
www.cs.put.poznan.pl/msterna/
INDUKCJA MATEMATYCZNA
Matematyka Dyskretna
 Małgorzata Sterna
FUNKCJA SILNIA
dla n  0, funkcja silnia zdefiniowana jest następująco:
O! = 1
n! = (n)·(n-1)·(n-2)·...·(3)·(2)·(1),
dla n  1
definicja rekurencyjna funkcji silnia:
O! = 1
n! = n·(n-1)!,
dla n  1
2
 Małgorzata Sterna
Matematyka Dyskretna
WSPÓŁCZYNNIK DWUMIANOWY
współczynnik dwumianowy
symbol Newtona
n!
n po k
n
n(n  1)(n  2)...(n  k  1)
 

k(k  1)(k  2)...1
 k  k! (n  k)!
występuje we wzorze na n-tą potęgę dwumianu (x+y)n:
n n
n
(x  y)  (x  y)  (x  y)  ...  (x  y)    x k ynk
k 0  k 
n
 3  k 3k  3  0 30  3  1 31  3  2 32  3  3 33
  x y
( x  y)     x y    x y    x y    x y
k 0 k 
 1
0
 2
3
3
3
 y3
 3xy 2
 3x 2 y
 x3
3
© Małgorzata Sterna
Matematyka Dyskretna
WSPÓŁCZYNNIK DWUMIANOWY
współczynnik dwumianowy („n po k”) określa liczbę
k-elementowych podzbiorów zbioru n-elementowego (kn):
n
n!
n  (n  1)  ...  (n  k  1)

 
1 2  ...  k
 k  (n  k)!k!
Podstawowe tożsamości:
n  n 
 

k  n  k 
 n   n  1  n  1
 


 k   k   k  1
n
 n  1
k   n

k 
 k  1
 m  n  k  m  n 

    

 k  s0 s  k  s 
reguła symetrii
reguła dodawania
reguła pochłaniania
tożsamość Cauchy’ego
4
© Małgorzata Sterna
Matematyka Dyskretna
WSPÓŁCZYNNIK DWUMIANOWY
Współczynnik dwumianowy występujący we wzorze na n-tą
potęgę dwumianu (x+y):
n n
n
(x  y)    x k ynk
k 0  k 
dla x=y=1
 n  k nk
n
  1 1  (1  1)
k 0 k 
n
określa liczność zbioru potęgowego
n
n
   2
k 0 k 
n
5
© Małgorzata Sterna
Matematyka Dyskretna
TRÓJKĄT PASCALA
obliczanie wartości współczynnika Newtona w oparciu o regułę
dodawania
 n  1


 k  1
 n  1


 k 
(x+y)0 =
1x0y0
(x+y)1 =
1x1y0 + 1x0y1
(x+y)2 =
1x2y0 + 2x1y1 + 1x0y2
(x+y)3 =
1x3y0 + 3x2y1 + 3x1y2 + 1x0y3
(x+y)4 = 1x4y0+ 4x3y1 + 6x2y2 + 4x1y3 + 1x0y4
n

k 

 
(x+y)5 = 1 x5y0+5 x4y1+10 x3y2 +10x2y3 +5 x1y4 +1 x0y5
współczynniki
n-tego wiersza:
n
 
0
n
 
 1
...
 n 


 n  1
n
 
n
6
 Małgorzata Sterna
Matematyka Dyskretna
WSPÓŁCZYNNIK WIELOMIANOWY
współczynnik dwumianowy to przykład
współczynnika wielomianowego
n

  n  n  k1  n  k1  k 2   n  k1  ...  kr 1 
...

   


k3
kr
 k1,k 2 ,...,kr   k1  k 2 

 
n!
k1!k 2!...  kr !
występującego w rozwinięciu wielomianu
kr
n

 k1 k2
(x1  x 2  ...  xr )n 

x1 x 2 ...xr

k1,k 2 ,...,kr 0  k1,k 2 ,..., kr 

k1k 2 ... kr n
dla n=k1+k2, k1=k
 n  n

 
 k1,k 2   k 
7
Matematyka Dyskretna
 Małgorzata Sterna
INDUKCJA MATEMATYCZNA
Indukcja matematyczna, to technika dowodzenia twierdzeń
oparta na specyficznych własnościach liczb całkowitych,
w szczególności na zasadzie dobrego uporządkowania.
8
Matematyka Dyskretna
 Małgorzata Sterna
ZASADA DOBREGO UPORZĄDKOWANIA
Każdy niepusty podzbiór zbioru liczb całkowitych dodatnich Z+,
zawiera element najmniejszy.
czyli
Zbiór Z+ jest dobrze uporządkowany.
Własność ta oznacz, że
Z+ = {xZ: x > 0}  Z+ = {xZ: x  1}
(analogiczną własność posiada każdy podzbiór zbioru liczb
całkowitych, np. zbiór liczb naturalnych N = {xZ: x  0}).
Zbiory np. liczb wymiernych lub rzeczywistych dodatnich
Q+={xQ: x > 0},
R+={xR: x > 0}
nie są dobrze uporządkowane.
9
 Małgorzata Sterna
Matematyka Dyskretna
ZASADA SKOŃCZONEJ INDUKCJI MATEMATYCZNEJ
(PIERWSZA ZASADA INDUKCJI MATEMATYCZNEJ)
Niech S(n) oznacza pewne zdanie otwarte, w którym występuje
zmienna n reprezentująca dodatnią liczbę całkowitą, nZ+.
S(1)    S(k)  S(k  1)   S(n)

kZ
 nZ
Jeśli
(1) S(1) jest prawdziwe
i
(2) dla dowolnego kZ+,
S(k+1) jest prawdziwe, jeśli S(k) jest prawdziwe,
to
S(n) jest prawdziwe dla wszystkich nZ+.
10
 Małgorzata Sterna
Matematyka Dyskretna
ZASADA SKOŃCZONEJ INDUKCJI MATEMATYCZNEJ
S(1)    S(k)  S(k  1)   S(n)

kZ
 nZ
W zasadzie skończonej indukcji matematycznej
S(1), to warunek początkowy,
założenie o prawdziwości S(k) dla dowolnego kZ+,
to hipoteza indukcyjna,
. S(k )  S(k  1) ,to krok indukcyjny.
k 1
Zasada indukcji matematycznej mówi, że
prawdziwość warunku początkowego
i kroku indukcyjnego
dowodzi prawdziwości hipotezy indukcyjnej.
11
 Małgorzata Sterna
Matematyka Dyskretna
ZASADA SKOŃCZONEJ INDUKCJI MATEMATYCZNEJ
warunek początkowy może być podany dla dowolnego elementu
n0Z+, który uznamy za pierwszy w procesie indukcyjnym
wówczas zasada przyjmuje postać:



S
(
n
)


S
(
k
)

S
(
k

1
)
  S(n)
 0 k n0


 nn0

Jeśli
(1) S(n0) jest prawdziwe dla pewnego n0Z+
i
(2) dla dowolnego kn0, kZ+,
S(k+1) jest prawdziwe, jeśli S(k) jest prawdziwe,
to
S(n) jest prawdziwe dla wszystkich nn0, nZ+.
12
 Małgorzata Sterna
Matematyka Dyskretna
DOWÓD INDUKCYJNY



S
(
n
)


S
(
k
)

S
(
k

1
)
  S(n)
 0 k n0


 nn0

Dowód oparty o zasadę indukcji matematycznej wymaga:
sformułowania hipotezy indukcyjnej – S(k),
dowiedzenia prawdziwości warunku początkowego S(n0),
dowiedzenia prawdziwości kroku indukcyjnego
(wykazując prawdziwość kroku indukcyjnego, nie dowodzi się
prawdziwości zdania S(k+1), ale prawdziwość implikacji
S(k)S(k+1)).
Dowód oparty o zasadę indukcji matematycznej, to pośrednie
dowiedzenie nieskończenie wielu twierdzeń (dla n0=1):
S(1), S(1)S(2), S(2)S(3), S(3)S(4), ....
13
 Małgorzata Sterna
Matematyka Dyskretna
DOWÓD INDUKCYJNY - PRZYKŁAD
Udowodnij, że:
n
   i  1  2  3  ...  n 
nZ i1
Dowód
n
sformułowanie hipotezy indukcyjnej:  S(n) :  i 
nZ 
i1
n(n  1)
2
n(n  1)
2
wykazanie prawdziwości warunku początkowego S(1), n=1:
dla n  1,S(1) :
1
i  1 
i1
n(n  1)
1(1  1)
2


2
2
2
krok indukcyjny - wykazanie prawdziwości implikacji S(k)S(k+1):
k(k  1) k 1 (k  1)(k  2)
  i 
 i 
2
2
kZ i1
i1
k
k 1
 i  1  2  ...  k  (k  1) 
i1

k
 i  (k  1) 
i1
k(k  1)  2(k  1)

2
z założenia o
prawdziwości S(k)
k(k  1)
 (k  1) 
2
(k  1)(k  2)
2
c.b.d.u.
14
Matematyka Dyskretna
 Małgorzata Sterna
DOWÓD SKOŃCZONEJ ZASADY INDUKCJI MATEMATYCZNEJ
Założenia:
niech S(n) będzie pewnym zdaniem spełniającym warunki (1) i (2) czyli:
S(1)    S(k)  S(k  1)

kZ

niech F będzie zbiorem postaci: F={tZ+: S(t) jest fałszywe}
niech F
Dowód przez sprowadzenie do sprzeczności:
z zasady dobrego uporządkowania wynika, że F zawiera element minimalny s,
sF
z założenia, S(n) spełnia warunek (1), więc S(1) jest zdaniem prawdziwym,
tym samym 1F i s1, czyli s > 1
ponieważ s > 1, to s-1 > 0 i s-1Z+
ponieważ s jest minimalnym elementem w F, to s-1F,
to S(s-1) jest zdaniem prawdziwym
z założenia, S(n) spełnia warunek (2),
czyli prawdziwość S(s-1) pociąga za sobą prawdziwość S((s-1)+1),
czyli S(s) jest zdaniem prawdziwym i sF
c.b.d.u.
otrzymana sprzeczność wynika z założenia, że F,
tym samym wykazano, że F= i S(n) jest spełnione dla wszystkich nZ+
15
Matematyka Dyskretna
 Małgorzata Sterna
ZASTOSOWANIE ZASADY INDUKCJI MATEMATYCZNEJ
Zasada indukcji matematycznej wykorzystywana jest w
rozumowaniu indukcyjnym, czyli w procesie formułowania faktów
ogólnych w oparciu o zbiór obserwacji.
Analiza przypadków, wynikania poszczególnych przypadków
jeden z drugiego, pozwala odgadnąć wzory ogólne i sugeruje
sposób przeprowadzenia kroku indukcyjnego w procesie ich
dowodzenia.
16
 Małgorzata Sterna
Matematyka Dyskretna
PRZYKŁAD
Dany jest ciąg liczb x0, x1, x2, ... zdefiniowany jako
x0=a
xn+1=2xn+b
dla a,b,nN. Czy można wyrazić xn jako funkcję parametru n?
n=0, x0 =a
= 1 a + 0 b = 1 a + (1-1)b = 20a + (20-1)b
n=1, x1 =2(a) + b
= 2 a + 1 b = 2 a + (2-1)b = 21a + (21-1)b
n=2, x2 =2(2a+b) +b
= 4 a + 3 b = 4 a + (4-1)b = 22a + (22-1)b
n=3, x3 =2(4a+3b) +b
= 8 a + 7 b = 8 a + (8-1)b = 23a + (23-1)b
n=4, x4 =2(8a+7b) +b
=16 a +15 b =16 a+ (16-1)b = 24a + (24-1)b
...
...
...
xn= 2na +(2n-1)b
17
 Małgorzata Sterna
Matematyka Dyskretna
PRZYKŁAD
Zaobserwowaną zależność można udowodnić korzystając z zasady
indukcji matematycznej.
Założenia:
x0=a
dla aN
xn+1=2xn+b
dla b,nN
Hipoteza indukcyjna: S(n): xn=2na+(2n-1)b dla każdego nN
Wykazanie prawdziwości warunku początkowego dla n=0, S(0):
S(0): x0 = 20a+(20-1)b =
= 1·a + 0·b =
=a
Krok indukcyjny - wykazanie prawdziwości S(k)S(k+1) dla dowolnego k,
czyli:
 x  2k a  (2k  1)b  x  2k 1a  (2k 1  1)b
kN
k
k 1
S(k+1): xk+1 = 2xk + b =
= 2(2ka+(2k-1)b) + b =
= 2·2ka+2·(2k-1)b + b =
= 2k+1a+(2k+1-2+1)b =
= 2k+1a+(2k+1-1)b
18
Matematyka Dyskretna
 Małgorzata Sterna
ZASADA SILNEJ INDUKCJI MATEMATYCZNEJ
(DRUGA ZASADA INDUKCJI MATEMATYCZNEJ)
Niech S(n) oznacza pewne zdanie otwarte, w którym występuje zmienna n
reprezentująca dodatnią liczbę całkowitą, nZ+.
Niech n0, n1Z+, n0n1.
Jeśli
(1) S(n0), S(n0+1), ..., S(n1-1), S(n1) są prawdziwe
i
(2) dla dowolnego kZ+, kn1 S(k+1) jest prawdziwe,
jeśli S(n0), S(n0+1), ..., S(k-1), S(k) są prawdziwe,
to
S(n) jest prawdziwe dla wszystkich nZ+, nn0.
S(n0 )  S(n0  1)  ...  S(n1) 


   S(n)
S(n0 )  S(n0  1)  ...  S(k)  S(k  1) nn0
 k

  n1
19
Matematyka Dyskretna
 Małgorzata Sterna
ZASADA SILNEJ INDUKCJI MATEMATYCZNEJ
S(n0 )  S(n0  1)  ...  S(n1) 


   S(n)
(2)   S(n0 )  S(n0  1)  ...  S(k )  S(k  1) 
nn0


k

n

 1
(1)
Podobnie jak w pierwszej zasadzie indukcji matematycznej:
(1) określa warunek początkowy
(2) krok indukcyjny
założenie o prawdziwości S(n0)S(n0+1)... S(k-1)S(k) dla kZ+ to
hipoteza indukcyjna.
20
Matematyka Dyskretna
 Małgorzata Sterna
ZASADA SILNEJ INDUKCJI MATEMATYCZNEJ
S(n0 )  S(n0  1)  ...  S(n1) 


   S(n)
S(n0 )  S(n0  1)  ...  S(k)  S(k  1) nn0
 k

  n1
Zasadę silnej indukcji matematycznej stosuje się:
jeśli prawdziwość analizowanego zdania wynika z prawdziwości
pewnych zdań poprzedzających (a nie wyłącznie z prawdziwości zdania
bezpośrednio poprzedzającego),
jeśli krok indukcyjny nie jest prawdziwy dla pewnych początkowych
wartości k (prawdziwość zdań S(k) dla tych wartości musi być
sprawdzona niezależnie w ramach dowodzenia warunku
początkowego),
w analizie definicji rekurencyjnych, w których pewne wyrazy określone
są za pomocą wyrazów innych niż bezpośrednio poprzedzający.
21
Matematyka Dyskretna
 Małgorzata Sterna
PRZYKŁAD
Dany jest ciąg liczb x0, x1, x2, ... zdefiniowany następująco:
x0=1, x1=2, x2=3, xn=xn-1+xn-2 +xn-3 dla nN, n3.
Twierdzenie:
S(n): xn3n, dla dowolnego nN
Dowód
Dowodzimy warunek początkowy wykazując, że zdania S(0), S(1), S(2) są
prawdziwe (n0=0, n1=2):
S(0): x0 =1  30 =1
S(1): x1 =2  31 =3
S(2): x2 =3  32 =9
W kroku indukcyjnym zakładamy prawdziwość zdań
S(0), S(1), ..., S(k-2), S(k-1), S(k) dla kN, k2,
aby wykazać prawdziwość S(k+1):
S(k+1): xk+1 = xk + xk-1+ xk-2  3k + 3k-1 + 3k-2  3k + 3k + 3k = 3(3k) = 3k+1
Krok indukcyjny wymagał założenia prawdziwości 3 zdań poprzedzających,
tzn. [S(k-2)  S(k-1)  S(k)]S(k+1)
22
Matematyka Dyskretna
 Małgorzata Sterna
ZASADA INDUKCJI MATEMATYCZNEJ
Pierwsza zasada (skończonej) indukcji matematycznej



S
(
n
)


S
(
k
)

S
(
k

1
)
  S(n)
 0 k n0


 nn0

i druga zasada (silnej) indukcji matematycznej
S(n0 )  S(n0  1)  ...  S(n1) 


   S(n)
S(n0 )  S(n0  1)  ...  S(k)  S(k  1) nn0
 k

n

 1
są równoważne, tzn. jeśli zaakceptujemy jedną z nich, to druga też jest poprawna.
2  1 Jeśli założymy prawdziwość wszystkich przypadków poprzedzających S(k+1),
tzn. S(n0), S(n0+1), ..., S(k-1), S(k),
to założyliśmy również prawdziwość przypadku bezpośrednio
poprzedzającego - S(k).
1  2 Dowód prawdziwości S’(n)=S(n0)S(n0+1)... S(n) w pierwszej
zasadzie indukcji
jest równoważny dowodowi S(n) w drugiej zasadzie.
23
 Małgorzata Sterna
Matematyka Dyskretna
POPRAWNOŚĆ DOWODU INDUKCYJNEGO
Poprawny dowód indukcyjny twierdzenia składa się z:
dowodu warunku początkowego,
dowodu kroku indukcyjnego.
Prawdziwość kroku indukcyjnego
  S(k)  S(k  1)
kZ
nie wystarcza do udowodnienia analizowanego twierdzenia.
Konieczne jest wykazanie prawdziwości warunku początkowego
S(n0), od którego proces indukcyjny może się rozpocząć.
24
 Małgorzata Sterna
Matematyka Dyskretna
PRZYKŁAD
Udowodnij, że dla dowolnego nZ+, liczba n2+5n+1 jest liczbą parzystą,
czyli udowodnij, że dla nZ+ istnieje rN takie, że n2+5n+1=2r.
Dowód kroku indukcyjnego S(k)S(k+1):
S(k):
dla kZ+
istnieje pN takie, że k2+5k+1=2p
S(k+1): dla (k+1)Z+
istnieje p’N takie, że (k+1)2+5(k+1)+1=2p’
S(k+1): (k+1)2 + 5(k+1) + 1 = k2 + 2k +1 +5k +5 +1 = (k2+5k+1) + (2k+6) =
= 2p + 2(k+3) = 2(p+k+3) = 2p’
Krok indukcyjny jest prawdziwy.
Dowód warunku początkowego:
n=1:
n2+5n+1 = 1+5+1
n=2:
n2+5n+1 = 4+10+1
n=3:
n2+5n+1 = 9+15+1
=7
 S(1) jest fałszywe
= 15
 S(2) jest fałszywe
= 25
 S(3) jest fałszywe
...
Nie istnieje żadna wartość nZ+, dla którego dowodzona własność zachodzi pomimo,
że krok indukcyjny jest prawdziwy.
Twierdzenie jest fałszywe!
25
Matematyka Dyskretna
 Małgorzata Sterna
WERYFIKACJA POPRAWNOŚCI PROGRAMÓW
Weryfikacja poprawności programu, to sprawdzenie czy program
rzeczywiście realizuje zadanie, które przed nim postawiono.
Weryfikacji poprawności nie można przeprowadzać wyłącznie poprzez
testowanie programu dla różnych danych wejściowych.
Program powinien być poprawny niezależnie od danych wejściowych.
26
 Małgorzata Sterna
Matematyka Dyskretna
PRZYKŁAD
Twierdzenie:
Następujący fragment programu oblicza wartość x(yn) dla zadanych
wartości parametrów, x,yR, nN:
start
while n0 do
begin
x:=xy;
n:=n-1;
end;
Answer:=x;
ustaw początkowe wartości
x,yR i nN
nie
n0
tak
x:=xy;
n:=n-1;
Answer:=x
27
 Małgorzata Sterna
Matematyka Dyskretna
SFORMUŁOWANIE
TWIERDZENIA
start
ustaw początkowe wartości
x,yR i nN
while n0 do
begin
x:=xy;
n:=n-1;
end;
Answer:=x;
nie
n0
tak
x:=xy;
n:=n-1;
Answer:=x
S(n): jeśli dla dowolnych x,yR, nN,
program rozpoczyna wykonywanie pętli „while” z wartością n,
to po ominięciu pętli (dla n=0)
lub n-krotnym wykonaniu 2 instrukcji (dla n>0)
zmienna Answer przyjmuje wartość x(yn).
Dowód prawdziwości S(n) oparty będzie o pierwszą zasadę indukcji matematycznej.
28
 Małgorzata Sterna
Matematyka Dyskretna
WARUNEK POCZĄTKOWY S(0)
S(n): jeśli dla dowolnych x,yR, nN, program rozpoczyna
wykonywanie pętli „while” z wartością n, to po ominięciu pętli
(dla n=0) lub n-krotnym wykonaniu 2 instrukcji (dla n>0)
zmienna Answer przyjmuje wartość x(yn).
Program rozpoczyna pętle „while” z wartością n=0,
start
ustaw
początkowe
wartości
x,yR i nN
podąża gałęzią „nie”
i kończy się z wartością
Answer = x
= x(1)
=x(y0)
=x(yn) dla n=0
Warunek początkowy S(0) jest prawdziwy.
nie
n0
tak
Answer:=x
x:=xy;
n:=n-1;
29
Matematyka Dyskretna
 Małgorzata Sterna
DOWÓD KROKU INDUKCYJNEGO S(k)S(k+1)
S(n): jeśli dla dowolnych x,yR, nN, program rozpoczyna
wykonywanie pętli „while” z wartością n, to po ominięciu pętli
(dla n=0) lub n-krotnym wykonaniu 2 instrukcji (dla n>0)
zmienna Answer przyjmuje wartość x(yn).
start
dla n =k+1 pętla „while” nie może być pominięta, gdyż n=k+1  1  0.
Instrukcje pętli zostaną więc wykonane co najmniej raz,
po ich ukończeniu nastąpi powrót na początek pętli
z wartościami:
x’ = xy
n’ = n-1=(k+1)-1 = k
Program rozpoczyna więc pętlę z n’=k, x’ i y, czyli zgodnie z
hipotezą indukcyjną S(k) kończy obliczenia z wartością:
Answer
= x’(yk)
= (xy)(yk)
= x(yk+1)
czyli krok indukcyjny S(k)S(k+1) jest prawdziwy dla
dowolnego kN i x,yR
ustaw
początkowe
wartości
x,yR i nN
nie
n0
tak
Answer:=x
x:=xy;
n:=n-1;
30
 Małgorzata Sterna
Matematyka Dyskretna
POPRAWNOŚĆ PROGRAMU
S(n): jeśli dla dowolnych x,yR, nN, program rozpoczyna
wykonywanie pętli „while” z wartością n, to po ominięciu pętli
(dla n=0) lub n-krotnym wykonaniu 2 instrukcji (dla n>0)
zmienna Answer przyjmuje wartość x(yn).
prawdziwość warunku początkowego S(0) i kroku indukcyjnego S(k)S(k+1)
dla dowolnych kN i x,yR dowodzi prawdziwości twierdzenia S(n) dla
dowolnych kN i x,yR
Następujący fragment programu oblicza wartość x(yn) dla zadanych wartości
parametrów, x,yR, nN:
while n0 do
begin
x:=xy;
n:=n-1;
end;
Answer:=x;
c.b.d.u.
31
 Małgorzata Sterna
Matematyka Dyskretna
NIEZMIENNIKI PĘTLI
Zdanie p jest niezmiennikiem pętli postaci
dopóki g,
wykonuj S
gdy spełnia następujący warunek:
„jeśli zdania p i g są prawdziwe, zanim zostaną wykonane kroki S, to zdanie p
będzie prawdziwe po wykonaniu S”.
while n0 do
begin
x:=xy;
n:=n-1;
end;
Answer:=x;
warunek dozoru pętli g
treść pętli S
wykonanie treści pętli, to
przebieg pętli lub iteracja
Zdanie S(n):
„Jeśli dla dowolnych x,yR, nN, program rozpoczyna wykonywanie pętli „while” z
wartością n, to po ominięciu pętli (dla n=0) lub n-krotnym wykonaniu 2 instrukcji (dla
n>0) zmienna Answer przyjmuje wartość x(yn).”
jest niezmiennikiem analizowanej pętli „while”.
32
Matematyka Dyskretna
 Małgorzata Sterna
TWIERDZENIE O NIEZMIENNIKACH PĘTLI
Przypuśćmy, że p jest niezmiennikiem pętli „dopóki g, wykonuj S” oraz,
że zdanie p jest prawdziwe, kiedykolwiek wchodzimy w pętle.
Wtedy zdanie p jest prawdziwe po każdej iteracji pętli.
Jeśli pętla się kończy, to zdanie p jest nadal prawdziwe,
a zdanie g jest fałszywe.
Niezmienniki pętli mogą być używane do:
projektowania algorytmów (określają cel do wykonania),
dowodzenia poprawności algorytmów.
Konstrukcja niezmiennika pętli jest przeważnie zadaniem trudnym. Wybrane
zdanie S(n) może:
nie być niezmiennikiem algorytmu, gdy metoda nie realizuje
postawionego zadania,
spełniać warunki narzucone na niezmiennik, ale metoda realizuje
błędnie postawione zadanie.
33