hko10_oblHydraul

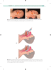
OBLICZENIA HYDRAULICZNE - metoda kolejnych przybliżeń
Obliczyć napełnienie t w kanale przy przepływie Q = 14 m3/s dla schematu pokazanego
na rysunku 1.
PRZYKŁAD
1
h
-1
1,3 m
1
-1
1,5 m
Dane do obliczeń:
t
PRZYKŁAD
4m
Ryc. 1. Schemat obliczeniowy
- Przepływ Q = 14 m3/s,
- Różnica wysokości zwierciadła wody na odcinku 158 m wynosi 33 cm,
- Wymiary koryta regulującego jak na schemacie.
ROZWIĄZANIE
PRZYKŁAD
1. Przepływ wody opisany jest równaniem
Q =υ ⋅F
(1)
gdzie: υ – średnia prędkość przepływu [ms-1],
F – pole powierzchni przekroju [m2]
1.1. Pole powierzchni przekroju jest sumą powierzchni F1 i F2
PRZYKŁAD
F = F1 + F2
F2 =
(2)
6,8 + 6,8 + (t − 1,3)
13,6 + (t − 1,3)
⋅ (t − 1,3) =
⋅ (t − 1,3)
2
2
F1 =
4 + 5,3
⋅ 1,3 = 6,045
2
PRZYKŁAD
Ryc. 2. Obliczenie pola powierzchni przekroju poprzecznego
F = 6,045 + [(6,8 + 0.5(t − 1,3) ) ⋅ (t − 1,3)] m2
1.2. Średnią prędkość przepływu wyliczymy ze wzoru
PRZYKŁAD
υ = C ⋅ Rh ⋅ I
(3)
gdzie: I - spadek linii energii (zwierciadła wody), I =
∆h 0,33
=
= 0,002
L
158
F
[m]
O
O – obwód zwilżony (ta część przekroju, która styka się z wodą) [m]
Rh - promień hydrauliczny. Rh =
PRZYKŁAD
O = t + 4 + 2 ⋅ 1,3 + 1,5 + 2 ⋅ (t − 1,3) = t + 7,34 + 2 ⋅ (t − 1,3) = 5,5 + 2.414t m
Rh =
6,045 + [(6,8 + 0.5(t − 1,3) ) ⋅ (t − 1,3)]
5,5 + 2.414t
1
1
⋅ Rh 6
n
n – współczynnik szorstkości; koryto ziemne dno nieumocnione, nieliczna roślinność
n = 0,029 [źródło: E. Kubrak, J. Kubrak, 2007, Podstawy obliczeń z mechaniki płynów,
Tab. 5.2, str. 238]
1
1
1
C=
⋅ Rh 6 = 34,48 Rh6
0,029
c - współczynnik prędkości wg Manninga, C =
PRZYKŁAD
2
 6,045 + [(6,8 + 0.5(t − 1,3) ) ⋅ (t − 1,3)]  3
υ = 34,48 ⋅ 
 ⋅ 0,002 m·s-1
5,5 + 2.414t


PRZYKŁAD
Podstawiam wyliczoną prędkość do wzoru (1) i dokonując odpowiednich podstawień uzyskujemy
2
 6,045 + [(6,8 + 0.5(t − 1,3) ) ⋅ (t − 1,3)]  3
14 = 34, 48 ⋅ 
 ⋅ 0,002 ⋅ (6,045 + [(6,8 + 0.5(t − 1,3) ) ⋅ (t − 1,3) ])
5,5 + 2.414 t


PRZYKŁAD
Powyższe równanie jest to równanie z jedną niewiadomą (napełnienie w kanale t), które można
rozwiązać poprzez przekształcenie do postaci t=..... Jest to jednak kłopotliwe dlatego do
rozwiązania tego typu zagadnień lepiej stosować metodę kolejnych przybliżeń. Metoda kolejnych
przybliżeń wydaje się skutecznym narzędziem przyśpieszającym proces szukania wartości t.
W metodzie tej minimum dwukrotnie przeprowadza się obliczenia przyjmując różne wartości
niewiadomej (w naszym przypadku zakładam t=2,0 m i t=1,7 m). Podstawiam do równania
wartość napełnienia t, porównuję wartości lewej i prawej strony równania. W przypadku braku
zgodności powtarzam obliczenia i wykonuje wykres (Ryc.3). Oszacowane prawidłowe
rozwiązanie odczytuje z wykresu, które następnie poddaje procedurze sprawdzającej.
PRZYKŁAD
2. Metoda kolejnych przybliżeń
Założenie 1: t=2,0 m
2
 6,045 + [(6,8 + 0.5( 2,0 − 1,3) ) ⋅ ( 2,0 − 1,3)]  3
14 = 34, 48 ⋅ 
 ⋅ 0,002 ⋅ (6,045 + [(6,8 + 0.5( 2,0 − 1,3) ) ⋅ ( 2,0 − 1,3) ])
5,5 + 2.414 ⋅ 2,0


PRZYKŁAD
Lewa strona równania ma wartość
Prawa strona równania po wyliczeniu
L=14.00
P=17.82
Ponieważ L≠P wykonuje kolejne obliczenie
Założenie 2: t=1,7 m
PRZYKŁAD
2
 6,045 + [(6,8 + 0.5(1,7 − 1,3) ) ⋅ (1,7 − 1,3) ]  3
14 = 34, 48 ⋅ 
 ⋅ 0,002 ⋅ (6,045 + [(6,8 + 0.5(1,7 − 1,3) ) ⋅ (1,7 − 1,3) ])
5,5 + 2.414 ⋅ 1,7


L=14.00
P=12.91
Ponieważ w dalszym ciągu L≠P wykonuje wykres
PRZYKŁAD
Punkt
rozwiązania
PRZYKŁAD
1.77
Ryc. 3. Sposób odczytania wartości napełnienia wody t
PRZYKŁAD
Z wykresu odczytuje wartość niewiadomej t jako rzut punktu przecięcia się linii na oś X.
Sprawdzenie: t = 1,77 m
L=14.00
P=14.00
L= P
PRZYKŁAD
Przy zadanych warunkach przepływu napełnienie w kanale wynosi t = 1,77 m