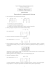G. Plebanek Programowanie Matematyczne nr 6 22.03.15

G. Plebanek
Programowanie Matematyczne
nr 6
22.03.15
Zagadnienie transportowe: metoda sympleks
Na razie milcząco zakładamy, że rozwiązania bazowe są niezdegenerowane; oznacza to,
że każde takie rozwiązanie ma wartości dodatnie w dokładnie n + m − 1 komórkach.
1. Znajdujemy dopuszczalne rozwiązanie bazowe (patrz lista 4-5); jest ono związane
z pewną bazą B, skladającą się z n + m − 1 komórek nie zawierających cyklu.
2. Obliczamy koszty zredukowane C(B)ij = cij + ui + vj , tak że C(B)ij = 0 dla
(i, j) ∈ B (patrz lista 3).
3. Jeżeli C(B)ij ­ 0 dla wszystkich (i, j) to dane DRB jest optymalne i to kończy
proces.
4. W przeciwnym razie ustalamy komórkę (i∗ , j ∗ ) z kosztem ujemnym. Komórki bazy
B wraz z tą wyrównioną zawierają dokładnie jeden cykl. Znajdujemy największa liczbę δ > 0, taką że można przyjąć xi∗j∗ = δ i tak pozmieniać wartości w
komórkach cyklu, aby otrzymać nowe DRB. Komórka (i∗ , j ∗ ) wchodzi do bazy a
dokładnie jedna komórka z niej wychodzi. Wracamy do 2.
W powyższej metodzie należy pamiętać aktualne rozwiązanie i aktualne koszty zredukowane; można się posłużyć formą zapisu jak w tym przykładzie:
0
2
0
5
1
2
0
0
4
−5
0
4
9
0
1 8
3
9
2
13
8
4
4
11
1
Wielkości w kratkach to koszty; kółka zaznaczają komórki bazy i w nich podano wartości
xij ; liczby poza tabelką to wartości popytu i podaży.
Uwaga: Gdy pojawiają się zdegenerowane DRB to postępujemy tak samo, z tym że
(i) należy pamiętać, że baza musi mieć n + m − 1 komórek, może więc zachodzić
potrzeba zaliczenia do bazy komórki z xij = 0;
(ii) może się okazac, że δ w punkcie 3 wynosi 0; wtedy nie zmieniamy wartości, a
jedynie zmieniamy bazę.
1. Dokonać iteracji w podanej powyżej tabeli i sprawdzić, czy nowe rozwiązanie jest optymalne.
2. Dokonać optymalizacji powyższą metodą w przykładach z list 4 i 5; przy obliczeniach
zapamiętywać wszystkie potrzebne dane w postaci opisanej powyżej.
Ogólne zagadnienie liniowe: Podstawy algorytmu sympleks
3. Rozważmy zagadnienie: zminimalizować x1 + x2 + 2x3 + 3x4 przy warunkach
3x1 + x2 + x3 + x4 = 2,
2x1 + x2 + x3 + 2x4 = 3,
x1 , x2 , x3 , x4 ­ 0.
Znaleźć rozwiązanie bazowe odpowiadające kolumnom A3 , A4 . Znaleźć kierunki bazowe
odpowiadające współrzędnym niebazowym. Znaleźć zredukowany wektor kosztów. Niech
d będzie kierunkiem bazowym odpowiadającym zmiennej x2 . Znaleźć θ∗ , tzn. taką liczbę
dodatnią θ∗ , że y = x + θ∗ d jest dopuszczalnym rozwiązaniem bazowym. Z którymi
kolumnami macierzy jest związane to rozwiązanie ? Sprawdzić, czy jest optymalne.
4. Rozważmy zagadnienie: zminimalizować 3x1 + 2x2 przy warunkach
x1
+ x3
x1 + 3x2
− x4
2x1 + x2
− x5
x1 , x2 , x3 , x4 , x5
= 4,
= 15,
= 10
­ 0.
Znaleźć rozwiązanie bazowe odpowiadające kolumnom A1 , A2 i A3 . Sprawdzić, czy to
rozwiązanie jest optymalne.
5. Rozważmy zagadnienie: zmaksymalizować x1 + 2x2 , przy warunkach
x1 + 3x2 ¬ 8,
x1 + x2 ¬ 4,
x1 , x2 ­ 0.
Sprowadzić zagadnienie do postaci standardowej. Znaleźć bazowe rozwiązanie dopuszczalne. Znaleźć rozwiązanie optymalne nowego zagadnienia, iterując metodę z poprzednich zadań.