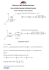Matematyka 2

Matematyka 2
Elementy analizy wektorowej cz V
Całka powierzchniowa zorientowana
Literatura
 M.Gewert, Z.Skoczylas; Elementy analizy
wektorowej; Oficyna Wydawnicza GiS,
Wrocław, 2000
 W.Żakowski, W.Kołodziej; Matematyka cz II;
WNT, Warszawa, 1984
 W.Leksiński, I.Nabiałek, W.Żakowski;
Matematyka dla studiów esperymentalnych;
WNT, Warszawa, 1981
 W.Stankiewicz; Zadanie z matematyki dla
wyższych uczelni technicznych cz II; PWN,
Warszawa, 1983
Płat powierzchniowy zorientowany
Definicja 1.
Płat powierzchniowy dwustronny, ma którym
wyróżniono jedną ze stron nazywamy płatem
zorientowanym. Wyróżnioną stronę płata nazywamy
stroną dodatnią. Płat zorientowany oznaczamy tym
samym symbolem co płat.
Płat powierzchniowy zorientowany przeciwnie do
płata  oznaczamy przez -.
Płat powierzchniowy zorientowany
Dla płatów zamkniętych w przestrzeni za stronę
dodatnią płata przyjmujemy z reguły jego stronę
zewnętrzną.
Dla płatów, które są wykresami funkcji z=f(x,y),
x=g(y,z), y=h(x,z) za stronę dodatnią przyjmujemy
zwykle górną część takiego płata.
Postać wersora normalnego płata
Fakt
Jeżeli płat gładki  jest wykresem funkcji
z=f(x,y),

gdzie (x,y)D to wersor normalny n tego płata
wystawiony w punkcie (x0,y0,z0) gdzie z0=f(x0,y0)
wyraża się wzorem
z
x0 , y0 
p

gdzie
x
 
p
q
1
n
,
,
 1  p2  q2 1  p2  q2 1  p2  q2

q




z
x0 , y0 
y

Wersor normalny n można przedstawić w postaci

n  cos  , cos  , cos   gdzie , ,  oznaczają kąty
między wersorem a dodatnimi częściami odpowiednio
osi OX, OY, OZ.
Definicja
Definicja 2.

Niech F  P, Q, R  będzie polem wektorowym na
płacie gładkim . Całką
 powierzchniową zorientowaną
z pola wektorowego F po płacie  definiujemy
wzorem.
 Px, y, z dydz  Qx, y, z dzdz  Rx, y, z dxdy 

  Px, y, z cos   Qx, y, z cos   Rx, y, z cos  dS

Zamiana na całkę podwójną
Twierdzenie 1.
Jeżeli gładki płat zorientowany  jest wykresem
funkcji
z=z(x,y), gdzie (x,y)D oraz pole wektorowe

F  P, Q, R  jest ciągłe na , to
 Px, y, z dydz  Qx, y, z dzdz  Rx, y, z dxdy 



  z 


z


  Rx, y, z x, y  dxdy
    Px, y, z x, y 
  Qx, y, z x, y 


x

y






D

Podobne równości mają miejsce gdy płat  jest
wykresem funkcji postaci x=x(y,z), y=y(x,z).
Zamiana na całkę podwójną
Przykład 1.
Obliczyć podaną całkę zorientowaną.
 x dydz  y dzdz  z dxdy

 wewnętrzna strona półsfery x2+y2+z2=R2, z≤0
Strumień pola wektorowego
Definicja 3.

Strumień pola wektorowego F  P, Q, R 
przez
powierzchnię zorientowaną  (ze strony ujemnej na
dodatnią) określamy wzorem
   Pdydz  Qdzdz  Rdxdy

Strumień pola wektorowego
Przykład
Obliczyć strumień pola wektorowego

F x, y, z   z, x, y 
przez powierzchnię  - górna strona płaszczyzny
3x+6y-2z=6 odciętej płaszczyznami układy
współrzędnych.
Wzór Gaussa-Ostrogradzkiego
Twierdzenie 2.
Jeżeli
1)  jest zorientowanym kawałkami gładkim płatem
zamkniętym, który jest brzegiem obszaru
domkniętego VR3 
2) pole wektorowe F  P, Q, R  jest różniczkowalne w
sposób ciągły na V,

to
 Pdydz  Qdzdz  Rdxdy   divF dV


V

Wzór Gaussa-Ostrogradzkiego
Przykład
Obliczyć całkę powierzchniową z podanego pola
wektorowego po wskazanym płacie zorientowanym.

F x, y, z   x, y, z 
 - zewnętrzna strona sfery o równaniu x2+y2+z2=9
Wzór Gaussa-Ostrogradzkiego
Przykład
Obliczyć całkę powierzchniową z podanego pola
wektorowego po wskazanym płacie zorientowanym.


F x, y, z   x  y, y 2  z, x  z

 - zewnętrzna strona powierzchni walca x2+y2=4
zamknięta płaszczyznami z=0 i z=1.
Wzór Stokesa
Twierdzenie 3.
Jeżeli
1)  jest płatem kawałkami gładkim zorientowanym,
którego brzeg  jest łukiem kawałkami gładkim
zorientowanym zgodnie
z orientacją płata 

2) pole wektorowe F  P, Q, R  jest różniczkowalne w
sposób ciągły na płacie  (łącznie z brzegiem )
to
 R Q 
 Q P 
 P R 



dxdy
Pdx

Qdy

Rdz


dydz


dzdx





  y z 
 z x 

 x y 


Wzór Stokesa
Przykład
Korzystając ze wzoru Stokesa obliczyć całkę
krzywoliniową
 x  y dx   y  z dy  z  x dz

jeżeli łuk  jest brzegiem zorientowanym dodatnio
względem płata  - dolna strona stożka z  x 2  y 2  1
odciętego płaszczyzną z=0.
Wzór Stokesa
Przykład
Obliczyć podaną całkę krzywoliniową z podanego pola
wektorowego po wskazanym łuku zorientowanym
oraz sprawdzić otrzymany wynik wykorzystując tw.
Stokesa.

F  2 x,3 y,4 z 
 - brzeg półsfery z  4  x 2  y 2
przebiegany w
stronę przeciwną do ruchu wskazówek zegara.
Zastosowania
• Objętość obszaru V ograniczonego płatem
zamkniętym 
• Ilość cieczy przepływającej w jednostce czasu przez
płat zorientowany 
• Parcie cieczy o ciężarze właściwym C na dodatnią
stronę płata zorientowanego , który jest zanurzony
w tej cieczy.
Elementy analizy
wektorowej cz V
Całka powierzchniowa
zorientowana