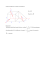1.1. Elementy działań na wektorach

Z fizyką w przyszłość
8
1.1. Elementy działań na wektorach
Wielkości fizyczne, które poznasz w rozszerzonym kursie fizyki, można podzielić na dwie
grupy: wielkości skalarne i wielkości wektorowe. Wielkościami skalarnymi są np. masa,
gęstość, droga, czas, temperatura. Wielkości wektorowe to np. przemieszczenie, prędkość,
przyspieszenie, siła.
Wielkość skalarną podajemy w postaci liczby z odpowiednią jednostką, np. m = 5 kg,
r = 1000 kg/m3, p = 1013 hPa, t = − 10°C. Wielkości te mogą być dodatnie lub ujemne. Są
też wielkości skalarne bezwymiarowe, np. współczynnik tarcia.
Wielkości wektorowe mają wartość (równą długości wektora, a więc zawsze dodatnią,
wyrażoną w odpowiednich jednostkach), kierunek i zwrot. Dla większości wielkości wektorowych, takich jak np. siła, podajemy też punkt zaczepienia (przyłożenia).
Na rysunku 1.1 przedstawiono wektory prędkości Księżyca w punktach A i B toru jego
 
ruchu wokół Ziemi. Są one różne: υ1 ≠ υ2, bo mają różne kierunki. Ich wartości są takie


same, co zapisujemy następująco: υ1 = υ2 lub u1 = u2.
A
Z
B
Rys. 1.1
Prędkości dwóch samochodów jadących w przeciwne strony (rys. 1.2) mogą mieć jednakowe lub różne wartości (u1 = u2 lub u1 ≠ u2). Leżą na prostych równoległych, więc mają
ten sam kierunek, ale przeciwne zwroty.
x
Rys. 1.2
Rozdział 1. Opis ruchu postępowego
9
Dodawanie i odejmowanie wektorów
Wektory możemy dodawać, czyli znajdować wektor wypadkowy. Jeśli dodawane wektory
mają jednakowe kierunki i zgodne zwroty, to wartość wektora wypadkowego jest sumą
wartości tych wektorów. Kierunek i zwrot wektora wypadkowego jest taki jak dodawanych wektorów (rys. 1.3). Jeśli dodawane wektory mają jednakowy kierunek, ale przeciwne
zwroty, wartość ich sumy obliczamy, odejmując od wartości dłuższego wektora wartość
wektora krótszego. Kierunek wypadkowej jest taki sam jak kierunek dodawanych wektorów, a zwrot wypadkowej jest zgodny ze zwrotem wektora o większej wartości (rys. 1.4).
a
a
b
b
a
b
a
b
c
d
c=a+b
d=a+b
Rys. 1.3
Rys. 1.4
 
Dla dowolnych dwóch wektorów a i b ich sumę znajdujemy następująco: rysujemy



wektor a, a następnie przesuwamy równolegle wektor b tak, by koniec wektora a był po

czątkiem wektora b. Suma to wektor o początku w początku wektora a i końcu w końcu

wektora b (rys. 1.5a).
a)
b)
a
b
a
b
a
a
b
w
k
b
k=a+b
w=a+b
Rys. 1.5
Przy dodawaniu wektorów o różnych kierunkach można stosować także tzw. regułę
równoległoboku (rys. 1.5b), jednak w przypadku dodawania większej liczby wektorów
pierwsza z tych metod (nazywana często metodą wieloboku) jest wygodniejsza. Sprawdź,
że w każdym przypadku kolejność, w której rysujemy dodawane wektory, nie wpływa na
wynik.
Z fizyką w przyszłość
10

Wektory odejmujemy, dodając do wektora a, od którego odejmujemy, wektor przeciwny

do odejmowanego wektora b (rys. 1.6).
a
b
a
b
c = a b = a + ( b)
c
Rys. 1.6
Mnożenie wektora przez liczbę

Wektor można pomnożyć lub podzielić przez liczbę. Jeśli wektor u pomnożymy przez
dodatnią liczbę k, to kierunek i zwrot wektora pozostają bez zmiany, a wartość jest równa


ku. Jeśli liczba k jest ujemna, zwrot wektora ku jest przeciwny do zwrotu wektora u.
Rozkładanie wektora na składowe
Każdy wektor można traktować jako sumę dwóch lub większej liczby wektorów. Można
go zatem rozłożyć na składowe wzdłuż określonych kierunków. W problemach fizycznych
wybór tych kierunków jest zwykle w jakiś sposób
F2
uzasadniony.
Rysunek 1.7 przedstawia lampę wiszącą na wyF1
F
sięgniku wykonanym z metalowych prętów, przymocowanych do ściany. Kierunki sił składowych
narzucone są więc przez sytuację fizyczną. Siły
działają wzdłuż metalowych prętów. Pręt poziomy
jest rozciągany, a ukośny zgniatany. Rozkładana
siła jest sumą swoich składowych:
Rys. 1.7

Rozważmy wektor a w dwuwymiarowym,
kartezjańskim układzie współrzędnych xy i rozłóżmy go na wektory składowe wzdłuż osi x i y
(rys. 1.8). Składowe wektora w danym układzie
współrzędnych to jego rzuty na osie tego układu.

 
Wektor a można więc zapisać jako sumę ax i ay .
  
a = a x +a y
  
F = F1 + F2
y
ay
a
ax
Rys. 1.8
x
Rozdział 1. Opis ruchu postępowego
11
Współrzędne wektora
Oprócz składowych wektora posługujemy się często pojęciem współrzędnych wektora.

Współrzędna ax wektora a na osi x, czyli tzw. „iksowa” współrzędna wektora
ax = a cos a
a współrzędna ay na osi y, czyli tzw. „igrekowa” współrzędna wektora (rys. 1.9)
ay = a sin a
y
ay
y
by
a
by
b
ay
ax
ax
x
bx
x
bx
bx < 0
by > 0
ax > 0
ay > 0
Rys. 1.9
Rys. 1.10
cx < 0
cy < 0
y
cx
dx > 0
dy < 0
y
cx
dx
dx
x
x
cy
d
dy
c
cy
Rys. 1.11
dy
Rys. 1.12
Znaki współrzędnych wektora zależą od kąta, który ten wektor tworzy z osiami x i y.
Na rysunkach 1.9, 1.10, 1.11 i 1.12 przedstawiono cztery różne przypadki położenia
wektora w układzie współrzędnych. Na osiach zaznaczono składowe wektorów (wektory)
kolorem niebieskim, a współrzędne (liczby) kolorem czerwonym.
 
Spójrz na rysunek 1.2. Wektory u1 i u2 mają taki sam kierunek. W takim przypadku
jako oś x wybieramy dowolnie zwróconą prostą równoległą do tych wektorów. Współrzędna wektora zwróconego zgodnie ze zwrotem osi jest dodatnia i równa wartości wektora, a współrzędna wektora zwróconego przeciwnie do osi jest ujemna i równa wartości
wektora ze znakiem minus. Tak więc u1x = u1 i u2x = − u2. Jeśli oś x zwrócimy przeciwnie
(zależy to wyłącznie od naszego wyboru), wtedy u1x = − u1, a u2x = u2.