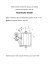Dezorientacja ziaren - Wydział Inżynierii Materiałowej

Politechnika Warszawska
Wydział Inżynierii Materiałowej
Laboratorium Zaawansowanych Metod Badania Materiałów
Instrukcja do ćwiczenia:
Dezorientacja Ziaren
wykonał: Grzegorz Słowiński
1
1. Wstęp
Umiejętność określenia wzajemnej orientacji ziaren (dezorientacji) może być przydatna
w trakcie prowadzenia badań materiałowych, np. podczas badania mechanizmów
odkształcenia plastycznego (przechodzenie poślizgu z ziarna do ziarna), zjawiska
bliźniakowania (wzajemna orientacja bliźniaków), podczas badań dotyczących struktury
granic ziarn, podczas badania wydzieleń.
1.1 Wykorzystanie TEM do określenia dezorientacji
Dezorientację określa się dla dwu ziaren, na podstawie dyfraktogramów z obu tych
ziaren. Podczas obserwacji w trybie mikroskopowym TEM odnajduje się obszar granicy
ziaren (i wykonuje się zdjęcie). Następnie ustawia się w polu widzenia ziarno 1, przełącza się
mikroskop na tryb dyfrakcyjny i wykonuje dyfraktogram (zdjęcie dyfrakcyjne) z obszaru
ziarna 1. Powraca się do trybu mikroskopowego, ustawia się w polu widzenia ziarno 2,
przełącza na tryb dyfrakcyjny i wykonuje się dyfraktogram ziarna 2.
Rys. 1. Trójka zdjęć z TEM. Mikroskopowe zdjęcie z obszaru granicy ziaren i dyfraktogramy z
obu ziaren. Dyfraktogramy posłużą do wyznaczenia wzajemnej orientacji ziaren. [Zdjęcia
wykonał Jan Kozubowski]
Dyfraktogramy trzeba następnie wywskaźnikować (co było tematem ćwiczenia na
LMBM i nie jest ujęte w tym ćwiczeniu) i przeprowadzić procedurę określenia dezorientacji
(na czym się skoncentrujemy).
2
2. Metody opisu wzajemnej orientacji ziaren
Wzajemną orientację ziaren można opisać podając:
•
Równoległe kierunki i/lub płaszczyzny w obu ziarnach
•
Kąty Euler'a
•
Oś i kąt obrotu
•
Macierz dezorientacji
3. Procedura wyznaczenia macierzy dezorientacji
W trakcie ćwiczenia studenci zapoznają z jedną z metod wyznaczania macierzy
dezorientacji i znajdują taką macierz na podstawie pary dyfraktogramów.
3.1. Wyznaczenie wersorów
Przed wyznaczeniem macierzy dezorientacji należy utworzyć bazę wersorów dla obu
ziaren w układzie laboratoryjnym. Jeżeli oznaczymy bazę wersorów dla ziarna 1: x1, y1, z1, a
dla ziarna 2: x2, y2, z2 to muszą zachodzić związki:
x1||x2, y1||y2, z1||z2
oraz
(x1×y1)·z1≠0 i
(x2×y2)·z2≠0 - (iloczyn mieszany wersorów danej bazy różny od zera, czyli wersory
nie leżą w jednej płaszczyźnie.)
Szczególnym przypadkiem jest, gdy posiadamy bazę ortogonalną, czyli z wersorami
wzajemnie prostopadłymi. Wtedy spełnione są warunki:
(x1×y1)·z1=1 i
(x2×y2)·z2=1
W naszym ćwiczeniu wyznacza się właśnie bazę ortogonalną, gdyż akurat jest to
najprostsze. Baza ortogonalna ma także tę zaletę, że może ułatwić dalsze obliczenia (co jest
pomocne przy braku komputera z odpowiednim programem matematycznym).
W trakcie ćwiczenia student otrzymuje dyfraktogramy dwu ziaren. Bazę wersorów
najwygodniej jest zbudować w oparciu o układ związany z TEM, na którym wykonano
zdjęcie, co w praktyce oznacza zbudowanie bazy wersorów w oparciu o boki obrazu
dyfrakcyjnego i wektor prostopadły (oś pasa dyfraktogramu).
Aby policzyć wektory X1, Y1(jeszcze nie wersory i w odróżnieniu od wersorów
oznaczane wielkimi literami), należy wykonać odpowiednią konstrukcję geometryczną i
skorzystać z praw dodawania wektorów, co najlepiej zilustruje rysunek.
3
Rys 2. Konstrukcja geometryczna dla policzenia wektora X.
4
Analogicznie należy wyznaczyć wektor Y1, prostopadły do X1. Należy zadbać, aby
konstrukcja geometryczna była możliwie duża i wykonana precyzyjnie, w przeciwnym razie
kierunki będą policzone ze zbyt dużą niedokładnością, co może utrudnić poprawne policzenie
macierzy.
Wektor Z1 to wektor określający oś pasa dyfraktogramu, jest dany, nie trzeba go
liczyć.
Po otrzymaniu wektorów X1, Y1, Z1 należy obliczyć odpowiednie wersory x1, y1, z1
(dodatek A).
Procedurę należy powtórzyć dla drugiego ziarna, aby otrzymać wersory x2, y2, z2.
3.2. Zapisanie równań
Posiadając bazy wersorów obu ziaren można zapisać 3 równania wektorowomacierzowe:
x2 = M·x1
(1.1)
y2 = M·y1
(1.2)
z2 = M·z1
(1.3),
gdzie M to macierz dezorientacji ziaren 1 i 2.
M
 a11 a12 a13 

 a21 a22 a23 
a a a
 31 32 33 
(1.4)
Rozwiązując powyższy układ oblicza się macierz dezorientacji M.
3.3. Metody rozwiązania układu
Obliczenia matematyczne można wykonać "na piechotę" lub skorzystać z pomocy
komputera (szczególnie zalecany jest program Mathcad), co potrafi wyśmienicie przyśpieszyć
i ułatwić rozwiązanie.
3.3.1. Metoda 1
Układ
x2 = M·x1
y2 = M·y1
z2 = M·z1,
należy zapisać w postaci skalarnej:
5
 x21 

 x22 
 x2
 3
 a11 a12 a13   x11 


 a21 a22 a23  ⋅ x12 
a a a

 31 32 33   x13 
(2.1)
 y21 

 y22 
 y2
 3
 a11 a12 a13   y11 


 a21 a22 a23  ⋅ y12 
a a a

 31 32 33   y13 
(2.2)
 z21 

 z22 
 z2
 3
 a11 a12 a13   z11 


 a21 a22 a23  ⋅ z12 
a a a

 31 32 33   z13 
(2.3) czyli,
x21
a11⋅x11 + a12⋅x12 + a13⋅x13
(3.1.1) z (2.1)
x22
a21⋅x11 + a22⋅x12 + a23⋅x13
(3.1.2) z (2.1)
x23
a31⋅x11 + a32⋅x12 + a33⋅x13
(3.1.2) z (2.1)
y21
a11⋅y11 + a12⋅y12 + a13⋅y13
(3.2.1) z (2.2)
y22
a21⋅y11 + a22⋅y12 + a23⋅y13
(3.2.2) z (2.2)
y23
a31⋅y11 + a32⋅y12 + a33⋅y13
(3.2.3) z (2.2)
z21
a11⋅z11 + a12⋅z12 + a13⋅z13
(3.3.1) z (2.3)
z22
a21⋅z11 + a22⋅z12 + a23⋅z13
(3.3.2) z (2.3)
z23
a31⋅z11 + a32⋅z12 + a33⋅z13
(3.3.3) z (2.3)
Zestawiając odpowiednio równania
x21
a11⋅x11 + a12⋅x12 + a13⋅x13
(3.1.1)
y21
a11⋅y11 + a12⋅y12 + a13⋅y13
(3.2.1)
z21
a11⋅z11 + a12⋅z12 + a13⋅z13
(3.3.1)
uzyskuje się układ 3 równań z niewiadomymi a11, a12, a13. Podobnie należy zestawić w
układy równania (3.1.2), (3.2.2), (3.3.2) oraz (3.1.3), (3.2.3), (3.3.3).
Rozwiązanie tych trzech układów trzech równań z trzema niewiadomymi daje w
wyniku macierz M.
6
3.3.2. Metoda 2
Układ trzech równań wektorowo-macierzowych należy zapisać jako jedno równanie
macierzowe
W2 = M·W1
(4.1)
 x21 y21 z21 

 x22 y22 z22 
 x2 y2 z2
 3 3 3
(4.2)
 x11 y11 z11 

 x12 y12 z12 
 x1 y1 z1
 3 3 3
(4.3)
gdzie
W2
W1
Mnożąc obie strony równania przez W1-1 otrzymuje się:
W2·W1-1 = M
(4.4)
w ogólnym przypadku policzenie macierzy odwrotnej jest dość skomplikowane, ale jeśli
korzystano z ortogonalnej bazy wersorów, to okazuje się, że W1-1=W1T.
3.3.3. Możliwe są także inne metody, zwłaszcza przy użyciu komputerowych programów
matematycznych, gdzie zazwyczaj wystarczy poprawnie wprowadzić układ równań
wektorowo-macierzowych i nakazać jego rozwiązanie.
4. Policzenie osi i kąta obrotu
4.1 Oś obrotu
Oś obrotu dana jest wzorem:
[n1, n2, n3] = [a32 - a23, a13 - a31, a21 - a12]
4.2 Kąt obrotu
Kąt obrotu należy obliczyć zgodnie z wzorem:
kąt
 tr( M) − 1  , gdzie tr(M) oznacza ślad macierzy (z ang. trace) i wyraża się
2


arccos
wzorem
tr(M) = a11 + a22 + a33
7
Dodatek A: Obliczenie wersora dla danego wektora
Jeżeli dany jest wektor X
X = [X1, X2, X3]
to równoległy doń wersor x liczy się zgodnie z wzorami
x = [X1/|X|, X2/|X|, X3/|X|], gdzie
(X1)2 + (X2)2 + (X3)2
X
8
Dodatek B: Iloczyn macierzy [na podstawie Tadeusz Trajdos, Matematyka część III, WNT,
Warszawa 1981, s.98-99]
W zbiorze macierzy wprowadzamy działanie zwane mnożeniem macierzy, oznaczane
symbolem D (zawsze pomijanym), zgodnie z definicją:
tzn. element iloczynu macierzy, znajdujący się w i-tym wierszu i k-tej kolumnie, jest
zbudowany z elementów aij i-tego wiersz pierwszej macierzy oraz elementów bjk k-tej
kolumny drugiej macierzy:
C = AB czyli
i≤m
k≤n
Działanie prowadzące od i-tego wiersz macierzy A i k-tej kolumny macierzy B do i,kelementu ich iloczynu AB,
AB przez analogie do skalarnego mnożenia wektorów w układzie
ortokartezjańskim, nazywamy mnożeniem skalarnym i-tego wiersza macierzy A przez k-tą
kolumnę macierzy B.
Zwracamy uwagę czytelnika na to, że mnożenie macierzy jest wykonalne wtedy i tylko
wtedy, gdy liczba kolumn mnożnej (oznaczona przez nas literą p) jest równa liczbie wierszy
mnożnika; otrzymujemy wtedy iloczyn będący macierzą o liczbie wierszy równej liczbie
wierszy mnożnej i liczbie kolumn równej liczbie kolumn mnożnika.
Przykłady:
a)
1 2 3 
 2 1 −1  
⋅ 4 5 6 

 0 −1 2  
7 8 9 
b)
 2 ⋅1 + 1 ⋅4 + (−1) ⋅7 2 ⋅2 + 1 ⋅5 + (−1) ⋅8 2 ⋅3 + 1 ⋅6 + (−1) ⋅9 


 0 ⋅1 + (−1) ⋅4 + 2 ⋅7 0 ⋅2 + ( −1) ⋅5 + 2 ⋅8 0 ⋅3 + ( −1) ⋅6 + 2 ⋅9 
 a11 a12 a13   x1 


a
a
a
⋅
 21 22 23   x2 
a a a

 31 32 33   x3 
 a11⋅x1 + a12⋅x2 + a13⋅x3 

 a21⋅x1 + a22⋅x2 + a23⋅x3 
 a ⋅x + a ⋅x + a ⋅x
 31 1 32 2 33 3 
9
 −1 1 3 

 10 11 12 
c)
 a11 a12 a13 

( x1 x2 x3 ) ⋅ a21 a22 a23 
a a a
 31 32 33 
( a11⋅x1 + x2⋅a21 + x3⋅a31
10
x1⋅a12 + a22⋅x2 + x3⋅a32 x1 ⋅a13 + x2⋅a23 + a33⋅x3 )
Dodatek C: Rozwiązanie układu trzech równań liniowych metodą Cramera
(wyznaczników)
Jeżeli mamy dany układ równań:
α 1⋅x + β 1⋅y + γ 1⋅z
Ω1
α 2⋅x + β 2⋅y + γ 2⋅z
Ω2
α 2⋅x + β 2⋅y + γ 2⋅z
Ω2
Należy policzyć wyznaczniki:
A≠0 (jeśli A=0, to układ jest nieoznaczony),
x, y, z dane są wzorami
x
Dx
A
y
Dy
z
A
Dz
A
Wyznacznik macierzy o wymiarach 3 na 3 liczy się zgodnie z wzorem:
11