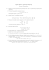Zaawansowane Metody Numeryczne 2006/07 — Zestaw 3 1

Zaawansowane Metody Numeryczne 2006/07 — Zestaw 3
1
Rosenbrock function z = (1-x)2 + 100(y-x2)2
1600
1400
1200
1000
800
600
400
200
03
2.5
2
2
1.5
1
1.5
y
0.5
1
0
-0.5
0.5
-1
0 -2
x
-1.5
Rysunek 1: Funkcja Rosenbrocka.
1. Obowiazuj
˛ a˛ zaległe zadania z poprzednich zestawów.
2. Znaleźć analitycznie minimum funkcji Rosenbrocka
f (x, y) = (1 − x)2 + 100(y − x2 )2 .
(1)
Przedstawić rozwini˛ecie tej funkcji w szereg Taylora wokół minimum z dokładnościa˛ do drugiego rz˛edu.
3N. Znaleźć numerycznie minimum funkcji Rosenbrocka (1) startujac
˛ z kilku-kilkunasto losowo
wybranych punktów. Za każdym razem przedstawić graficznie drog˛e, jaka˛ przebywa algorytm,
to jest kolejne położenia znalezione w metodzie gradientów sprz˛eżonych lub zmiennej metryki,
lub też zaakceptowane kroki w metodzie Levenberga-Marquardta.
4N. Dany jest układ równań
9x2 + 36y 2 + 4z 2
2
2
x − 2y − 20z
2
2
x −y +z
2
=
36 ,
(2a)
=
0,
(2b)
=
0.
(2c)
Rozwiazać
˛ ten układ numerycznie za pomoca˛
(a) metody Newtona
(b) metody Broydena
startujac
˛ z punktów (x, y, z) = (±1, ±1, 0). Znaleźć rozwiazanie
˛
z dokładnościa˛ 10−6 . Porównać koszt numeryczny obu metod.
Zaawansowane Metody Numeryczne 2006/07 — Zestaw 3
2
5N. Spróbować wyznaczyć granice basenów atrakcji poszczególnych rozwiazań
˛
układu (2) w metodzie Newtona. Znalezione granice przedstawić graficznie. Jak zachowuje si˛e metoda gdy
punkt poczatkowy
˛
leży bardzo blisko takiej granicy?
6. Przedyskutować sposoby rozwiazywania
˛
równania
x = ϕ(y + αx) ,
(3)
gdzie x, y ∈ RN , natomiast ϕ:RN → RN jest dostatecznie gładka˛ funkcja.˛
7N. Rozważmy nast˛epujac
˛ a˛ iteracj˛e:
θ n+1 = θ n + h k(θ n ) ,
h
(1)
(2)
(N )
gdzie θ n = θn , θn , . . . , θn
iT
(4)
oraz
k(θ n ) = f θ n + 21 h k(θ n ) ,
(5)
przy czym k ∈ RN , f = [f1 , f2 , . . . , fN ],
fi (θ) = ωi −
N
g X
sin θ(i) − θ(j) .
N j=1
(6)
Przyjać
˛ N = 256, ωi = (i − N/2)/N , h = 1/128. Przeprowadzić 1024 kroki iteracji (4),
(i)
zakładajac,
˛ że {θ0 }N
e wielkość
i=1 sa˛ rozłożone losowo w przedziale [0, 2π]. Jak zachowuje si˛
rn =
N
1 X
exp iθn(j)
N j=1
(7)
w funkcji n oraz g, g ∈ (0, 1)? Wyniki przedstawić graficznie. Uwaga: zanim zaczniecie
państwo coś kodować, prosz˛e przyjrzeć si˛e sumie w (6) i pomyśleć jak szybko obliczyć t˛e
sum˛e i jaki brać punkt startowy w każdym kroku iteracji.
PFG