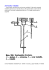Wahadło, zagadnienie..

Wahadło (bez tłumienia)
Jak pamiętamy z poprzednich spotkań równanie wahadła bez uwzględnienia sił oporu (tłumienia) jest
następujące
d 2
g
  sin  ,
2
dt
(1.1)
gdzie  (t )  kąt wychylenia w chwili t , g  przyspieszenie grawitacyjne w pobliżu ziemi (dla Ziemi
g  9,81m / s 2 ),
 długość wahadła. Zauważmy, że ruch wahadła w tym przypadku nie zależy od
jego masy! Aby równanie (1.1) opisywało jednoznacznie ruch należy je uzupełnić o warunki
początkowe: początkowe wychylenie 0 i początkową prędkość:
 (0)  0 ,

 (0)  0 .
(1.2)
Ponieważ opis (1.1) zawiera współrzędną biegunową, więc początkową prędkość liniową, 0 ,
wygodnie jest zamienić na prędkość kątową:
d
 0  0 . Tak więc matematycznie cały problem
dt
opisu ruchu wahadła ma postać
 d 2
g
 dt 2   sin  ,

 (0)  0 ,
 d
 (0)  0 .
 dt
(1.3)
Niestety problemu (1.3) nie można rozwiązać analitycznie (tzn. „wzorem”), i dlatego musimy
stosować metody numeryczne. Jednym z takich sposobów jest procedura Verleta. Implementacja tej
procedury zastosowanej do problemu (1.3) jest zawarta w pliku wahadło.cpp.
Wahadło z tłumieniem
Jeżeli dodamy bardziej realistyczne założenie, że ruch odbywa się w ośrodku stawiającym opór, to
uzyskamy model wahadła z tłumieniem. Dla małej kulki i niedużych prędkości można przyjąć, że opór
ten jest proporcjonalny do prędkości
Fopór  k .
(1.4)
Drugie prawo dynamiki Newtona ma teraz postać
ma  mg  k ,
(1.5)
gdzie k  0 jest współczynnikiem oporu. Zależy on od własności ośrodka (np. gęstość, temperatura) i
rozmiaru kulki.
Jeżeli teraz uwzględnimy, że ruch odbywa się po okręgu, oraz że prędkość kątowa jest proporcjonalna
do liniowej, to otrzymamy następująca modyfikację równania (1.3)
 d 2
g
k d
 dt 2   sin   m dt ,

 (0)  0 ,
 d
 (0)  0 .
 dt
(1.6)
Do numerycznego rozwiązywania równania (1.6) nie będziemy używać metody Verleta (zasadniczo
używa się jej w do modeli, w których siła nie zależy od prędkości; gdy siła zależy od prędkości można
dokonać pewnej modyfikacji tej metody). Wykorzystamy natomiast prostą metodę Eulera, która
bazuje na przybliżeniu
dv v

dt t
(1.7)
1
v 1
1

F 
 F  v (t  t )  v (t )   F (t )  t.
m
t m
m

(1.8)
a
więc
a
Zagadnienie dwóch ciał
Zagadnienie to dotyczy opisu ruchu dwóch ciał niebieskich we wzajemnie wytwarzanym polu
grawitacyjnym. Typowym przykładem może być ruch planety wokół Słońca, gdy zaniedbamy wpływ
pozostałych planet . Okazuje się, że zadanie to można sprowadzić do następującego opisu:
1) Ruch odbywa się w jednej płaszczyźnie.
2) Jedno ciało znajduje się w środku układu odniesienia a drugie krąży wokół niego pod
wpływem siły grawitacyjnej wytwarzanej przez ciało pierwsze.
Ponieważ siła grawitacji wynosi
Fgraw  G
Mm
rˆ,
r2
(1.9)
gdzie r̂  wektor jednostkowy (wersor) leżący na prostej łączącej środki obu ciał, więc ruch ciała m
w polu ciała M umieszczonego w środku układu jest opisany równaniem, stała grawitacji
3
G  6, 67 1011  kgms2 


ma  G
Uwzględniając, że
Mm
rˆ.
r2
(1.10)
r (t )  [ x(t ), y (t )], v (t )  [ x(t ), y(t )], a (t )  [ x(t ), y(t )],
r
r 2  x 2  y 2 , rˆ   [ x / x 2  y 2 , y / x 2  y 2 ],
r
możemy układ (1.10) opisujący ruch planetu zapisać tak
x
 dvx
,
 dt  ax  GM 2
2 3/ 2
x

y




y
 dv y  a  GM
.
y
2
2 3/ 2
 dt
x

y



(1.11)
Dla Ziemi mamy M  5,97 1024 [kg ], zatem GM  39,82 1013 [m3 / s 2 ]. Do symulacji wygodnie
będzie jednak użyć większych jednostek niż metry dlatego będziemy się posługiwać jednostka równą
mr  10 km  104 m. Stąd
m  104 mr , m3  1012 mr ,
co daje wartość
GM  39,82 1013 m3 / s 2  39,82 1013 1012 mr3 / s 2  398, 2 mr3 / s 2 .
Uwzględniając te jednostkę możemy opisać ruch ciała w polu grawitacyjnym Ziemi wzorami
x
 dvx
,
 dt  ax  GM 2
2 3/ 2
x

y




y
 dv y  a  GM
,
y
2
2 3/ 2
 dt
x

y



gdzie GM  398, 2 oraz jednostka długości wynosi 10 km (zatem x  1 oznacza 10 km itd.).
(1.12)