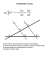po bo emu - Edupress

nauczanie matematyki
Twierdzenie
Pitagorasa
po bożemu
Jaki jest naturalny dowód
jednego z najbardziej znanych
twierdzeń – twierdzenia
Pitagorasa? Przypominamy
znane rozumowanie oparte
na podobieństwio trójkątów.
n
JANUSZ KARKUT
W
jednym z numerów czasopisma „Nauczyciele i Matematyka” (nr 12, zima 1994) trzy
artykuły dotyczą uzasadnienia twierdzenia Talesa: Spodnie Talesa Krzysztofa Mostowskiego, Lekcja o twierdzeniu Talesa
Heleny Chłopek i Marka Gnyra oraz Stefana Turnaua Twierdzenie Talesa „po Bożemu”. I choć dwa pierwsze projekty lekcji wydają się pociągające, głosowałbym
za trzecim przychylając się do opinii Stefana Turnaua: „Twierdzenie Talesa można wyprowadzić ze wzorów na pole równoległoboku lub trójkąta. Dla mnie to
jednak rodzaj matematycznego wywracania kota ogonem do góry. Uważam, że
odkrycie twierdzenia Talesa i pierwsze
uzasadnienie jego prawdziwości powinno
odbywać się po bożemu: kot na czterech
łapach i ogon na swoim miejscu.
Dodajmy, że tak dowodzi twierdzenie
Talesa Euklides w swoich Elementach.
30
1/2004
To o twierdzeniu Talesa. A co z twierdzeniem Pitagorasa?
Czy cechy podobieństwa trójkątów
(prostokątnych) to istotnie tak trudne zagadnienie, że trzeba przed nim uciekać
w popłochu, gubiąc po drodze „majteczki” i „spodnie”? Przekonajmy się. Proponuję następujące rozwiązanie.
Niech pracą domową będzie wykonanie rysunków dwóch przystających trójkątów prostokątnych, takich np. jak ten
na rysunku.
Już na lekcji proponujemy przyjęcie
wspólnych oznaczeń i rozcięcie jednego
z trójkątów wzdłuż jego wysokości poprowadzonej z wierzchołka kąta prostego.
Uzupełniamy oznaczenia:
Otrzymane w ten sposób dwa trójkąty
prostokątne układamy następnie w trójkącie, który nie został rozcięty, tak jak na
rysunku.
35
35
nauczanie matematyki
W ten sposób jesteśmy w pełni przygotowani do postawienia pytania o podobieństwo trzech (prostokątnych) trójkątów. „Przecież to widać!” – mówią uczniowie przypominając, że:
Jeżeli dwa kąty jednego trójkąta są przystające do dwóch kątów drugiego trójkąta, to te trójkąty są podobne.
Mając trzy pary trójkątów podobnych
piszemy następujące proporcje:
b = q a = p h = q
c b c a
p h
Łatwo też pokazać, że jeżeli a i b są
liczbami dodatnimi, to ab Ë a + b . Od2
czytujemy to bezpośrednio z następującego rysunku.
Korzystając z podstawowej własności proporcji mamy:
b2 = c × q, a2 = c × p, h2 = p × q.
Dodając stronami równości a2 = c × p
i b2 = c × q otrzymujemy
a2 + b2 = c(p + q) = c × c,
czyli
a2 + b2 = c2.
Podobne rozwiązanie znajdujemy w
starym podręczniku geometrii Bolesława
Iwaszkiewicza. Czy rozwiązanie to jest
złe? Przecież inni stosują je nadal (łatwo
znaleźć je np. w aktualnych podręcznikach niemieckich) nie czując potrzeby
zmian. Może to całkiem dobra partytura?
Używając równości b2 = c ×q, a2 = c ×p,
h2 = p × q możemy pokazać konstrukcje
pozwalające przekształcić dany prostokąt
na kwadrat o takim samym polu powierzchni. Mamy bowiem:
36
36
Myślę, że wartością przedstawionego
sposobu dowodu twierdzenia Pitagorasa
jest możliwość wykorzystania go do wielu innych konstrukcji, że nie jest to metoda wymyślona przez matematyków jedynie dla innych matematyków. Daje ona
też możliwość sporządzenia planu metodycznego zajęć, w którym czynności
uczniów są zapisane wcześniej niż czynq
ności nauczyciela.
JANUSZ KARKUT
nauczyciel w Zespole Szkół im. R. Traugutta
w Lipnie.
matematyka
31