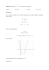Funkcje i ich własności

Transkrypt

materiał pochodzi ze strony matematyka.pisz.pl
Narysuj wykres następującej funkcji.
f (x) =
−2x − 3 dla x ∈ h−5, −1)
x2 − 2
dla x ∈ h−1, 3)
x
4
5
4
7
8
y
2
3
5
0
1
x
1
1
1
3
2
y
0
2
8
9
12
To przyporządkownie nie jest funkcją, ponieważ liczbie 4 zostały przyporządkowane
dwie liczby 2 i 5.
Rozwiązanie:
y = x2 − 2
y = −2x − 3
x
−5
−3
−2
x
−1
0
1
2
y
7
3
1
y
−1
−2
−1
2
To przyporządkownie nie jest funkcją, ponieważ liczbie 1 zostały przyporządkowane
trzy liczby 0, 2 i 8.
Funkcja jest
wzorem f (x) = x2 − 3x + 5. Oblicz jej wartości dla argumentów 4, 0,
√ określona
√
3
−4, 1 + 2, 5 − 2.
Rozwiązanie:
y
f (4) = 42 − 3 · 4 + 5 = 16 − 12 + 5 = 9
f (0) = 02 − 3 · 0 + 5 = 5
f (−4) = (−4)2 − 3 · (−4) + 5 = 16 + 12 + 5 = 33
f (1 +
x
3
7
2
8
y
4
8
9
0
1
x
2
3
5
8
9
y
1
4
1
1
10
√
2)2 − 3 · (1 +
√
√
√
√
2) + 5 = 1 + 2 2 + 2 − 3 − 3 2 + 5 = 5 − 2
Funkcja f : {−3, −2, 0, 1} → R każdej liczbie ze zbioru {−3, −2, 0, 1} przyporządkowuje
jej kwadrat pomniejszony o 4. Określ funkcję za pomocą grafu, tabelki, wzoru. Podaj zbiór
wartości funkcji.
Rozwiązanie:
1
2) = (1 +
√
√
√
√
√
√
3
3
3
3
3
3
f ( 5 − 2) = ( 5 − 2)2 − 3 · ( 5 − 2) + 5 = 25 − 4 5 + 4 − 3 5 + 6 + 5 =
√
√
3
3
= 15 − 7 5 + 25
Czy następujące określone tabelką przyporządkowania są funkcjami?
x
√
To przyporządkownie jest funkcją, ponieważ każdej liczbie ze zbioru x-ów jest przyporządkowana dokładnie jedna liczba ze
zbioru y -ów.
Rozwiązanie:
To przyporządkownie jest funkcją, ponieważ każdej liczbie ze zbioru x-ów jest przyporządkowana dokładnie jedna liczba ze
zbioru y -ów. Nie szkodzi, że wartość 1 powtarza się trzy razy.
wartości tej funkcji dla argumentów: −3, −2, 0, 1
— matematyka.pisz.pl —
Wzór tej funkcji:
f (x) = x2 − 4
1
f (−3) = (−3)2 − 4 = 9 − 4
f (−3) = 5
f (0) = 02 − 4 = 0 − 4
f (0) = −4
f (−2) = (−2)2 − 4 = 4 − 4
f (1) = 12 − 4 = 1 − 4
f (1) = −3
f (−2) = 0
Rozwiązanie:
y = |x|
y=2
x
−3
−2
0
1
y
5
0
−4
−3
−3
x
−4
−3
x
−2
0
2
y
2
2
y
2
0
2
5
−2
0
0
−4
1
−3
y = 2x − 2
y
zbiór wartości funkcji: {5, 0, −4, −3} 2
x
3
4
5
y
4
6
8
y = 2x − 3
Rozwiązanie:
x
x
−1
0
2
y
−5
−3
1
y
x
y = 2|x|
Rozwiązanie:

dla x ∈ h−4, −2)
2
f (x) = |x|
dla x ∈ h−2, 2i

2x − 2 dla x ∈ (2, ∞)
2
x
−2
−1
0
1
2
y
4
2
0
2
4
Dziedzina funkcji
y
Dziedzina funkcji to zbiór zawierający wszystkie liczby, które możemy podstawić do wzoru funkcji. Możemy ją też odczytać z wykresu funkcji.
Oznaczenia: D Df X
Przykłady:
x
y=
y=
√
D = h0, ∞), ponieważ nie można pierwiastkować liczb ujemnych.
x
1
x
D = R \ {0}, ponieważ nie można dzielić przez 0 ( x1 = 1 : x).
y
f (x) =
-2
5x
D = h−2, 5)
−1 dla x ∈ (−∞, −3) ∪ (3, ∞)
−|x| + 2 dla x ∈ h−3, 3i
Rozwiązanie:
y = −1
Znajdź dziedzinę funkcji.
y = −|x| + 2
f (x) =
x
−6
−4
4
6
x
−3
−2
0
2
3
y
−1
−1
−1
−1
y
−1
0
2
0
−1
√
3x + 9
Rozwiązanie:
Wyznaczamy dziedzinę wiedząc, że liczb ujemnych nie możemy pierwiastkować.
3x + 9 0
3x −9 / : 3
y
x −3
Odp. D = h−3, ∞)
f (x) =
x
√
4 − 2x
Rozwiązanie:
Wyznaczamy dziedzinę wiedząc, że liczb ujemnych nie możemy pierwiastkować.
4 − 2x 0
3
−2x −4 / : (−2)
Odczytaj dziedzinę funkcji o podanych wykresach.
x¬2
Rozwiązanie:
y
Odp. D = (−∞, 2i
5
4
3
2
1
−5−4−3−2−1
5
f (x) =
2x + 6
1 2 3 4 5
−1
−2
−3
−4
−5
dziedzina: D = (−4, 4i
x
Rozwiązanie:
dziedzina funkcji
y
Mianownik nie może być równy 0, ponieważ nie wolno dzielić przez 0.
5
4
3
2
1
2x + 6 = 0
2x = −6 / : 2
−5−4−3−2−1
x = −3
Odp. D = R \ {−3}
1 2 3 4 5
−1
−2
−3
−4
−5
dziedzina: D = h−2, ∞)
x
y
f (x) =
5
4
3
2
1
4
x(x + 3)
Rozwiązanie:
−5−4−3−2−1
dziedzina funkcji
Mianownik nie może być równy 0, ponieważ nie wolno dzielić przez 0.
x=0
1 2 3 4 5
−1
−2
−3
−4
−5
dziedzina: D = R x
x(x + 3) = 0
lub x + 3 = 0
x = −3
Odp. D = R \ {0, −3}
Zbiór wartości
Zbiór wartości to zbiór zawierający wszystkie liczby, które możemy otrzymać ze wzoru funkcji.
4
Możemy go też odczytać z wykresu funkcji.
Oznaczenia: ZW, ZWf , Zf , Y
y
Przykłady:
y = x2
ZW = h0, ∞), ponieważ podnosząc do kwadratu
otrzymujemy liczby nieujemne.
y =x+1
ZW = R,
funkcja dla żadnego argumentu
nie przyjmuje wartości −5
5
4
3
2
1
−5−4−3−2−1
ponieważ możemy otrzymać dowolną liczbę
wstawiając odpowiednią za x.
1 2 3 4 5
−1
−2
−3
−4
−5
x
f (−1, 5) = 0
f (3) = 0
f (−1, 8) = 2
f (5) = 2
y
4
x
ZW = h−2, 4)
y
-2
5
4
3
2
1
−5−4−3−2−1
Odczytaj z wykresów funkcji dla jakich argumentów, wartości funkcji wynoszą −5, 0, 2
f (−4) = −5
1 2 3 4 5
−1
−2
−3
−4
−5
x
f (−2) = 0
f (−1) = 2
Rozwiązanie:
Miejsce zerowe
y
f (3) = −5
5
4
3
2
1
−5−4−3−2−1
1 2 3 4 5
−1
−2
−3
−4
−5
x
f (−3) = 0
f (1) = 0
f (−2) = 2
f (0) = 2
Miejsce zerowe to liczba, która podstawiona do wzoru funkcji daje wartość równą 0. Miejsce
zerowe możemy też odczytać z wykresu funkcji.
Przykłady:
5
y =x+2
x0 = −2, ponieważ podstawiając −2 za x otrzymujemy 0.
y = 2x − 6
x0 = 3,
ponieważ podstawiając 3 za x otrzymujemy 0.
y
x1 = 0
x0 = 1
x
1
i
x2 = 2
Odp. Funkcja y = x2 − 2x ma dwa miejsce zerowe: x1 = 0 i x2 = 2.
y=
0=
√
√
2x − 6
2x − 6
0 = 2x − 6
−2x = −6
: (−2)
x0 = 3
Oblicz miejsze zerowe funkcji.
y = x2 − 4
y = 3x − 2
y = x2 − 2x
y=
√
Odp. Funkcja y =
2x − 6
√
2x − 6 ma jedno miejsce zerowe: x0 = 3.
Rozwiązanie:
Oblicz miejsce zerowe funkcji.
Wyznaczając miejsce zerowe szukam dla jakiego x mam y = 0.
y=
y = 3x − 2
0 = 3x − 2
y=
2
3
x2 − 6
x2 + 3
3x
x+2
Na początku szukam dziedziny tej funkcji.
2
3.
x+2=0
x = −2
y = x2 − 4
Mianownik nie może być równa 0, a tak jest dla x = −2, dlatego dziedzina funkcji to x ∈
R \ {−2}. Wyznaczając miejsce zerowe szukam dla jakiego x mam y = 0.
Odp. Miejsce zerowe funkcji y = 3x − 2 to x0 =
0 = x2 − 4
4 = x2
x2 = 4
x1 = −2
y=
Rozwiązanie:
2 = 3x
3x = 2
:3
x=
3x
x+2
i
3x
x+2
0=
3x
x+2
0 = 3x
x2 = 2
3x = 0
x0 = 0
2
Odp. Funkcja y = x − 4 ma dwa miejsce zerowe: x1 = −2 i x2 = 2.
:3
Odp. Wynik 0 należy do dziedziny funkcji. Funkcja y =
zerowe: x0 = 0.
y = x2 − 2x
0 = x2 − 2x
0 = x(x − 2)
x(x − 2) = 0
y=
y=
6
x2 − 6
x2 + 3
3x
x+2
ma jedno miejsce
Na początku szukam dziedziny tej funkcji.
y
5
4
3
2
1
x2 + 3 = 0
x2 = −3
−5−4−3−2−1
To równanie nia ma rozwiązania, dlatego dziedzina funkcji są wszystkie liczby rzeczywiste.
Wyznaczając miejsce zerowe szukam dla jakiego x mam y = 0.
y=
x2 −6
x2 +3
0=
x2 −6
x2 +3
x2 = 6
Odp. Funkcja y =
x2 −6
x2 +3
6
i
−5−4−3−2−1
√
x2 = − 6
ma dwa miejsca zerowe: x1 =
1 2 3 4 5
−1
−2
−3
−4
−5
x
5
4
3
2
1
6 = x2
x1 =
x1 = −1, 5; x2 = 3
y
0 = x2 − 6
√
miejsca zerowe:
√
miejsca zerowe:
x1 = −2
1 2 3 4 5
−1
−2
−3
−4
−5
x
√
6 i x2 = − 6.
Wyznacz miejsca zerowe funkcji o podanych wykresach.
Monotoniczność
Rozwiązanie:
Monotoniczność oznacza najczęściej, że funkcja jest rosnąca, malejąca lub stała.
y
5
4
3
2
1
−5−4−3−2−1
1 2 3 4 5
−1
−2
−3
−4
−5
miejsca zerowe:
y
f (x2 )
x1 = −3, x2 = 1
Funkcja
rosnąca:
x
Definicja funkcji rosnącej:
x2 x
x1
f (x1 )
7
Dla każdego x1 < x2 : f (x1 ) < f (x2 )
y
y
f (x1 )
Funkcja
malejąca:
x2 x
f (x2 )
x1
funkcja jest:
5
4
3
2
1
Definicja funkcji malejącej:
Dla każdego x1 < x2 : f (x1 ) > f (x2 )
−5−4−3−2−1
y
1 2 3 4 5
−1
−2
−3
−4
−5
malejąca dla x ∈ h−2, −1i
stała dla x ∈ h−1, 2i
x
rosnąca dla x ∈ h2, ∞)
c
Funkcja
stała:
Definicja funkcji stałej:
x
Dla każdego x: f (x) = c
y
5
4
3
2
1
−5−4−3−2−1
1 2 3 4 5
−1
−2
−3
−4
−5
funkcja jest:
rosnąca dla x ∈ (−∞, 1i
x
stała dla x ∈ h1, ∞)
Wyznacz przedziały monotoniczności dla funkcji o podanych wykresach.
Odczytaj z wykresu najmniejszą i największą wartość funkcji.
Rozwiązanie:
Rozwiązanie:
y
y
funkcja jest:
5
4
3
2
1
−5−4−3−2−1
1 2 3 4 5
−1
−2
−3
−4
−5
5
4
3
2
1
rosnaca dla x ∈ (−4, −1i
malejąca dla x ∈ h−1, 3i
x
−5−4−3−2−1
rosnąca dla x ∈ h3, 4i
8
1 2 3 4 5
−1
−2
−3
−4
−5
Największa wartość:
ymax = 3
Minimalna wartość: ymin = −5
x
y
y
5
4
3
2
1
−5−4−3−2−1
1
Funkcja nie ma największa wartości.
Najmniejsza wartość: ymin = −2
1 2 3 4 5
−1
−2
−3
−4
−5
-4
funkcja nie jest różnowartościowa, ponieważ
dla −4 i 3 wartość wynosi tyle samo.
x
3
x
Czy funkcje o podanych wykresach są różnowartościowe?
Rozwiązanie:
y
5
4
3
2
1
−5−4−3−2−1
Maksymalna wartość:
ymax = 4
Funkcja nie ma najmniejszej wartości.
1 2 3 4 5
−1
−2
−3
−4
−5
x
−5−4−3−2−1
y
y
y
5
4
3
2
1
5
4
3
2
1
5
4
3
2
1
1 2 3 4 5
−1
−2
−3
−4
−5
funkcja nie jest
różnowartościowa
x
−5−4−3−2−1
1 2 3 4 5
−1
−2
−3
−4
−5
x
−5−4−3−2−1
funkcja nie jest
różnowartościowa
1 2 3 4 5
−1
−2
−3
−4
−5
x
funkcja jest
różnowartościowa
Parzystość i nieparzystość
Różnowartościowość
Funkcja jest parzysta, jeżeli dla dowolnych liczb przeciwnych wartość funkcji wynosi tyle samo.
Lewa strona wykresu jest odbiciem prawej.
Funkcja jest różnowartościowa, jeżeli nie ma takich dwóch liczb, dla których wartość funkcji
wynosi tyle samo.
f (−x) = f (x)
y
Przykłady:
y
Funkcja parzysta, ponieważ dla liczb przeciwnych
(np −3, 3) wartość wynosi tyle samo.
2
-3
x
3
x
Przykłady funkcji parzystych:
y = |x|
funkcja różnowartościowa
y = x2
y = cos x
Funkcja jest nieparzysta, jeżeli dla dowolnych liczb przeciwnych wartości funkcji są też przeciwne.
9
Zadania + Rozwiązania
Lewa strona wykresu jest odwróconym odbiciem prawej.
Wskaż wykresy funkcji okresowych i wartość ich okresu podstawowego.
f (−x) = −f (x)
y
y
y
Funkcja nieparzysta, ponieważ dla liczb przeciwnych
(np −5, 5) wartości też są przeciwne.
4
-5
5
x
1
x
1
x
1
x
Przykłady funkcji nieparzystych:
-4
y = x3
y=
1
x
y
y = sin x
y
1
x
y
Funkcja nie jest ani parzysta, ani nieparzysta.
Tak jest z większością funkcji.
Wskaż wykresy funkcji okresowych i wartość ich okresu podstawowego.
x
Rozwiązanie:
y
Funkcja jest okresowa.
Okres podstawowy: T = 4
1
Okresowość funkcji
Funkcja jest okresowa, jeżeli jej wykres da się podzielić na nieskończenie wiele identycznych
części.
|
{z
T =4
x
}
y
y
Funkcja nie jest okresowa.
x
1
x
y
Okres funkcji - długość jednej części na jakie został podzielony wykres.
Funkcja jest okresowa.
Przykłady funkcji okresowych:
y = sin x
y = cos x
y = tg x
y = ctg x
Okres podstawowy: T = 2
y = x − [x]
1
x
| {z }
T =2
10
y
Różnowartościowość:
funkcja nie jest różnowartościowa
Parzystość:
funkcja nie jest ani parzysta ani nieparzysta
Okresowość:
funkcja nie jest okresowa
Funkcja nie jest okresowa.
x
1
Dla poniższej funkcji określ dziedzinę, zbiór wartości, miejsca zerowe, monotoniczność, różnowartościowość, parzystość, okresowość.
Zadania + Rozwiązania
Dla poniższych funkcji określ dziedzinę, zbiór wartości, miejsca zerowe, monotoniczność, różnowartościowość, parzystość, okresowość.
y
y
y
y
1
1
x
1
x
1
Dla poniższej funkcji określ dziedzinę, zbiór wartości, miejsca zerowe, monotoniczność, różnowartościowość, parzystość, okresowość.
Rozwiązanie:
y
1
x
Rozwiązanie:
Dziedzina:
D=R
Zbiór wartości:
ZW = (−∞, 3i
Miejsce zerowe:
x0 ≈ −3 lub x0 ≈ 1, 5
Monotoniczność:
funkcja jest przedziałami monotoniczna
rosnąca w przedziale (−∞, −1i
malejąca w przedziale h−1, ∞)
x
x
Dziedzina:
D = h−4, 4)
Zbiór wartości:
ZW = h−4, 3i
Miejsce zerowe:
x0 ≈ −2,8 lub x0 = 3
Monotoniczność:
malejąca w przedziale h−4, −1i
stała w przedziale h−1, 1i
rosnąca w przedziale h1, 4)
Parzystość:
Okresowość:
Dla poniższej funkcji określ dziedzinę, zbiór wartości, miejsca zerowe, monotoniczność, różno11
Wykres funkcji f (x + a) otrzymuję przez przesunięcie wykresu f (x) o a w lewo.
wartościowość, parzystość, okresowość.
Przykłady:
y
1
y
y
1
1
x
1
f (x)
x
f (x − 4)
x
1
f (x + 2)
f (x)
Rozwiązanie:
Dziedzina:
D = h−3, ∞)
Przesunięcie wykresu wzdłuż osi y
Zbiór wartości:
ZW = h−4, ∞)
Wykres funkcji f (x) + b otrzymuję przez przesunięcie wykresu f (x) o b do góry.
Wykres funkcji f (x) − b otrzymuję przez przesunięcie wykresu f (x) o b do dołu.
Miejsce zerowe:
x0 ≈ −2, 1 lub x0 = 0 lub x0 ≈ 2, 3
Przykłady:
Monotoniczność:
f (x) + 3
rosnąca w przedziale h−3, −1i
malejąca w przedziale h−1, 1i
rosnąca w przedziale h1, ∞)
y
y
f (x)
f (x)
1
1
1
x
1
x
f (x) − 2
Parzystość:
Okresowość:
Przesunięcie wykresu wzdłuż osi x
Narysuj wykres funkcji y = x2 a następnie przekształć go tak aby otrzymać wykres funkcji
Wykres funkcji f (x − a) otrzymuję przez przesunięcie wykresu f (x) o a w prawo.
12
y = (x − 3)2 , y = (x + 1)2 , y = x2 + 4, y = x2 − 3.
Rozwiązanie:
x
−2
−1
0
1
2
y = x2
4
1
0
1
4
Wykres y = x2 + 4 otrzymuję przesuwając y = x2 o 4 w górę.
y
y
x
x
Wykres y = (x − 3)2 otrzymuję przesuwając y = x2 o 3 w prawo.
y
Wykres y = x2 − 3 otrzymuję przesuwając y = x2 o 3 w dół.
y
x
2
Wykres y = (x + 1)2 = (x − (−1)) otrzymuję przesuwając y = x2 o 1 w lewo.
x
y
x
13
Narysuj wykres funkcji y =
y=
1
x−2 ,
y=
1
x+3 ,
1
x
y=
a następnie przekształć go tak aby otrzymać wykres funkcji:
1
x
+ 1, y =
1
x
− 1.
Wykres y =
Rozwiązanie:
y=
x
−2
−1
− 12
1
2
1
2
1
x
− 12
−1
−2
2
1
1
2
1
x+3
=
1
x−(−3)
otrzymuję przesuwając y =
1
x
o 3 w lewo.
y
y
1
1
x
1
1
x
Wykres y =
Wykres y =
1
x−2
1
x
1
x
+ 1 otrzymuję przesuwając y =
1
x
o 1 w górę.
o 2 w prawo.
y
y
1
1
1
x
1
14
x
y
Wykres y =
1
x
− 1 otrzymuję przesuwając y =
1
x
o 1 w dół.
y = f (x + 1)
y = f (x)
1
y
1
x
x
1
Wykres y = f (x − 2) otrzymuję przesuwając wykres y = f (x) o 2 w prawo. y
y = f (x − 2)
y = f (x)
1
1
x
Rysunek przedstawia wykres funkcji y = f (x).
y
Wykres y = f (x) + 1 otrzymuję przesuwając wykres y = f (x) o 1 do góry. y = f (x)
1
1
x
y
y = f (x) + 1
y = f (x)
1
1
x
Narysuj wykresy funkcji:
y = f (x + 1),
y = f (x − 2),
y = f (x) + 1,
y = f (x) − 3,
y = f (x + 2) − 1,
y = f (x − 3) − 2,
y = f (x − 1) + 1.
Wykres y = f (x) − 3 otrzymuję przesuwając wykres y = f (x) o 3 do dołu. Rozwiązanie:
Wykres y = f (x + 1) otrzymuję przesuwając wykres y = f (x) o 1 w lewo. — matematyka.pisz.pl —
15
y
y
y = f (x − 1) + 1
y = f (x)
y = f (x)
1
1
x
1
1
x
y = f (x) − 3
Wykres y = f (x+2)−1 otrzymuję przesuwając wykres y = f (x) o 2 w lewo i 1 do dołu. y
Odbicie wykresu względem osi x
y = f (x)
1
x
1
Wykres funkcji −f (x) otrzymuję przez odbicie f (x) względem osi x. Wykresy f (x) i −f (x)
są symetryczne względem osi x.
y = f (x + 2) − 1
y
f (x)
Wykres y = f (x − 3) − 2 otrzymuję przesuwając wykres y = f (x) o 3 w prawo i 2 do
dołu. 1
1
y
x
−f (x)
y = f (x)
1
x
1
y = f (x − 3) − 2
Odbicie wykresu względem osi y
Wykres y = f (x − 1) + 1 otrzymuję przesuwając wykres y = f (x) o 1 w prawo i 1 do
góry. — matematyka.pisz.pl —
Wykres funkcji f (−x) otrzymuję przez odbicie f (x) względem osi y . Wykresy f (x) i f (−x)
są symetryczne względem osi y .
16
y
f (x)
y
f (−x)
f (x)
1
1
|f (x)|
1
x
1
Odbicie wykresu względem początku układu współrzędnych
x
Przesuwanie wykresu funkcji
Wykres funkcji
f (x − a) + b
Wykres funkcji −f (−x) otrzymuję przez odbicie f (x) względem początku układu współrzędnych. Wykresy f (x) i −f (−x) są symetryczne względem początku układu współrzędnych.
otrzymujemy przez narysowanie funkcji f (x) i przesunięciu jej o wektor [a, b].
y
Przykłady:
f (x)
y
y
y
y
y
y
y
1
1
x
−f (−x)
= |x − 3| + 2
= (x − 2)2 −4
= (x + 1)3 + 2
= (x + 5)2 −3
= x2 + 1
= (x − 2)2
2
= x+3
−1
rysujemy y = |x| i przesuwamy o wektor [3, 2]
y
y
y
y
y
y
= x2
= x3
= x2
= x2
= x2
= x2
[2, −4]
[−1, 2]
[−5, −3]
[0, 1]
[2, 0]
[−3, −1]
Pierwsza współrzędna wektora ma przeciwny znak niż liczba przy x, druga współrzędna ma
znak taki sam jak liczba na końcu.
Wykres wartości bezwzględnej z funkcji.
Narysuj wykres funkcji
Wykres funkcji |f (x)| otrzymuję przez odbicie części wykresu f (x) znajdującej się pod osią x.
y = |x − 3| + 2
17
Rozwiązanie:
przesuwanie funkcji o wektor
Wykres y = |x − 3| + 2 otrzymuję przesuwając y = |x| o wektor [3, 2].
x
y = |x|
−2
−1
0
1
2
2
1
0
1
2
y
y = |x|
y = |x + 1| − 2 x
y
y = |x − 3| + 2
y = |x|
y = (x − 2)2 − 1
x
Rozwiązanie:
Wykres y = (x − 2)2 −1 otrzymuję przesuwając y = x2 o wektor [2, −1].
x
−2
−1
0
1
2
2
4
1
0
1
4
y=x
y
y = |x + 1| − 2
Rozwiązanie:
x
Wykres y = |x + 1|−2 otrzymuję przesuwając y = |x| o wektor [−1, −2].
x
y = |x|
−2
−1
0
1
2
2
1
0
1
2
18
y=
1
−1
x+3
y
√
y=
Rozwiązanie:
x−2+3
Wykres y =
1
x+3 −1
y=
1
x
o wektor [−3, −1].
x
−2
−1
− 12
1
x
− 12
−1
−2
y=
1
2
1
2
2
1
1
2
√
x
x
y
Zapisz wzór funkcji f przesuniętej o wektor ~
u.
1
x
y=
1
x
y = x2 ~u = [2, 3]
y=
y = x3 ~u = [−1, 4]
y = |x| ~u = [0, −7]
~u = [−3, −5]
y = sin x ~u = − 21 , 0
y = 2x ~u = [0, 8]
Rozwiązanie:
x
funkcja przesunięta o wektor
y=
1
x+3
2
−1
y=x
[2, 3]
y = (x − 2)2 + 3
y = x3
[−1, 4]
y = (x − (−1))3 + 4 = (x + 1)3 + 4
[−3, −5]
y=
y = |x|
[0, −7]
y = |x|−7
y = sin x
1 −2, 0
y = sin(x − (− 12 )) = sin(x + 12 )
y = 2x
[0, 8]
y = 2x + 8
y=
y=
√
x−2+3
Rozwiązanie:
Wykres y =
√
x − 2 + 3 otrzymuję przesuwając y =
√
1
x
1
x−(−3)
−5=
1
x+3
−5
x o wektor [2, 3].
y=
√
x
0
1
4
9
x
0
1
2
3
Naszkicuj w jednym układzie współrzędnych wykresy funkcji f (x) = 2x+1 oraz g(x) = x+1
x .
Na podstawie wykonanego rysunku określ liczbę ujemnych rozwiązań równania f (x) = g(x).
19
Wykres f (x) = 2x+1 otrzymuję przez przesunięcie f (x) = 2x o wektor [−1, 0]
x
−2
−1
0
1
2
1
4
1
2
1
2
4
x
2
1
y = + 1
x
1
y = +1
x
Rozwiązanie:
y
y
y
x
x
x
i na podstawie rysunku okreRysuję na jednym wykresie f (x) = 2x+1 i g(x) = x+1
x
ślam liczbę ujemnych rozwiązań równania f (x) = g(x).
y
x + 1
g(x) = x x
Na początek narysuję wykres
y=
x+1
x
Wykresy przecinają się w trzech punktach, ale tylko dwa punkty przecięcia są dla x < 0.
y=
Wykres y =
x+1
x 1
1
1
= + =1+ = +1
x
x x
x
x
Odp. Równanie f (x) = g(x) ma dwa ujemne rozwiązania.
1
1
+ 1 otrzymuję przez przesunięcie y = o wektor [0, 1]
x
x
x
−2
−1
− 12
1
2
1
2
1
x
− 12
−1
−2
2
1
1
2
Rysunek przedstawia fragment wykresu funkcji liniowej f . Wykres funkcji g jest obrazem wykresu funkcji f otrzymanym za pomocą przesunięcia o wektor ~
u = [2, 1]. Wyznacz miejsce
zerowe funkcji g .
20
Rozwiązanie:
nazywamy odwrotnie proporcjonalnymi.
y
B0
3
2
A −1
Dziedzina: R \ {0}
Zbiór wartości: R \ {0} B f
A0 1
−6 −5 −4 −3
g
Przykłady:
1
−1
2
3
4
5
6
Czas przejazdu t z miasta do miasta jest odwrotnie proporcjonalny do prędkości v : t =
x
s
v
Liczba litrów benzyny n jest odwrotnie proporcjonalna do ceny c, jeżeli tankujemy za każdym
razem za tą samą sumę s:
0
Przesuwając A = (−2, 0) o wektor ~
u = [2, 1] otrzymuję A = (0, 1)
Przesuwając B = (3, 2)
o wektor ~
u = [2, 1] otrzymuję B 0 = (5, 3)
n=
s
c
Wykresem proporcjonalności odwrotnej y =
Równanie prostej przechodzącej przez punkty A0 = (0, 1) i B 0 = (5, 3)
a
jest hiperbola:
x
y
(y − 1) (5 − 0) − (3 − 1) (x − 0) = 0
(y − 1)5 − 2x = 0
y
a>0
a<0
5y − 5 − 2x = 0
5y = 2x + 5
.
x
:5
x
y = 52 x + 1
Wzór funkcji g :
y = 25 x + 1
Wyznaczam miejsce zerowe
2
x+1
5
. 2
2
− x=1
: −
5
5
5
x = −1 ·
2
0=
x = −2
Czy wielkości x i y są odwrotnie proporcjonalne?
Rozwiązanie:
1
2
x
−2
1
2
1
2
y
1
2
−2
−1
− 21
Przkształcam wzór proporcjanonalności odwrotnej
Odp. x0 = −2 12
y=
Proporcjonalność odwrotna
Wielkości związane zależnością
y=
a
x
·x
y·x=a
a 6= 0
a
x
x·y =a
21
Pary liczb są odwrotnie proporcjonalne, jeżeli ich iloczyn a jest taki sam.
−2 ·
1
2
Rozwiązanie:
= −1
y=
1
2
x
−2
−1
− 21
1
2
1
2
1
x
− 12
−1
−2
2
1
1
2
· (−2) = −1
y
1 · (−1) = −1
2 · − 21 = −1
Odp. Wielkości x i y są odwrotnie proporcjonalne.
x
x
−5
−1
1
5
y
−2
−8
8
2
−5 · (−2) = 10
dziedzina
zbiór wartości
miejsce zerowe
monotoniczność
−1 · (−8) = 8
Dalej już nie trzeba sprawdzać, bo dla dwóch pierwszych par iloczyn jest różny.
D = R \ {0}
ZW = R \ {0}
nie ma
malejąca w przedziałach (−∞, 0) i (0, ∞)
funkcja jest różnowartościowa
funkcja jest nieparzysta
Odp. Wielkości x i y nie są odwrotnie proporcjonalne.
różnowartościowość
parzystość
okresowość
Narysuj wykres funkcji i wypisz jej własności:
Narysuj wykres funkcji i wypisz jej własności:
y=
1
x
y=
22
−2
x
Rozwiązanie:
x
y=
−2
x
−2
−1
1
2
1
2
−2
−1
y
x
dziedzina
zbiór wartości
miejsce zerowe
monotoniczność
różnowartościowość
parzystość
okresowość
D = R \ {0}
ZW = R \ {0}
nie ma
rosnąca w przedziałach (−∞, 0) i (0, ∞)
funkcja jest różnowartościowa
funkcja jest nieparzysta
23

Funkcje i ich własności

Transkrypt

Podobne dokumenty

Zadanie 23 Funkcja 4 jest rosnąca w przedziale A. 0

Zadanie Napisz wzór funkcji wykładniczej , gdzie 0, wiedząc, że do

+ − = 5 2 )( x x x xf dla dla dla 5 5,0 0 > ∈ ≤ x x x 4 )( −−= x xf − − = 2

Temat: Tworzymy wykres kolumnowy i kołowy. Wykres umożliwia

Zestaw nr 3

PRACA DOMOWA nr 6

własności funkcji - zlotow

FUNKCJE – powtórzenie przed egzaminem 1. Na

Zestaw II. Funkcja liniowa 1. Naszkicuj wykres funkcji