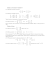Zadania z procesów stochastycznych. Zadanie. Niech X1,X2

Zadania z procesów stochastycznych.
Zadanie. Niech X1 , X2 , ... będą wynikami prób Bernoulliego, to znaczy niezależnymi zmiennymi losowymi o rozkładzie P (Xn = 1) = p, P (Xn = 0) = 1 − p = q, przy czym p 6= q. Określmy
Sn = X1 + X2 + ... + Xn oraz Fn = σ(X1 , X2 , ..., Xn ). Sprawdzić rachunkiem, że ciąg
!∞
S n
q
p
, Fn
n=1
jest martyngałem.
Egzamin z Procesów Stochastycznych 2006
1. Niech (Xn )∞
n=1 będzie łańcuchem Markowa, przy czym pij = P (Xn+1 = j |Xn = i). Za pomocą
liczb pij opisać prawdopodobieństwa P (Xn = j |Xn+1 = i) oraz P (Xn = j |Xn+2 = k).



2. Dana jest macierz przejścia w jednym kroku łańcucha Markowa: 


1
2
1
4
1
8
1
16
1
2
0
0
0
0
3
4
0
0

0

0 

7
8
15
16
.

Czy ten łańcuch jest okresowy? Czy jest ergodyczny (to znaczy, czy istnieje granica lim P n )? Jeśli tak,
to obliczyć rozkład stacjonarny.
3. Niech λ > 0. Załóżmy, że w czystym procesie urodzin mamy λn = n · λ oraz P (X0 = 2) = 1.
Układając i rozwiązując odpowiednie równania różniczkowe, obliczyć P (Xt = 3).
4. Niech (Xt )t­0 będzie procesem Poissona o intensywności λ > 0. Obliczyć:
a) P (X3 = 2, X5 = 3), b) P (X5 = 3 |X3 = 2), c) P (X3 = 2 |X5 = 3).
5. Niech (Wt )t­0 będzie procesem Wienera. Dla 0 ¬ t ¬ 1 obliczyć funkcję korelacji procesu Xt =
Wt − tW1 .
6. Niech Ω = [0, 1], a X = x2 . Obliczyć E(X|F), gdy F jest najmniejszym σ-ciałem zawierającym
zbiory [0, 21 ] oraz ( 14 , 1].
Zadania na piątkę
∞
1. Niech (Xn )∞
n=1 będzie łańcuchem Markowa. Czy proces (X2n )n=1 (gdzie występują tylko zmienne o
indeksach parzystych) jest łańcuchem Markowa? Jeśli odpowiedź brzmi TAK, to udowodnić to, jeśli
brzmi NIE, to wskazać kontrprzykład.
2. Ergodyczny łańcuch Markowa o dwóch stanach ma rozkład stacjonarny (p, 1 − p), 0 < p < 1. Jak
wygląda macierz przejścia tego łańcucha?