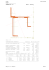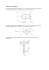22. parametry geometryczne figur płaskich

Transkrypt

Dodatek
22. PARAMETRY GEOMETRYCZNE FIGUR PŁASKICH
1
Í Ï Î
22.
PARAMETRY GEOMETRYCZNE FIGUR PŁASKICH
22.1. DEFINICJE
Rozdział 22. dotyczy figur płaskich o równomiernym rozkładzie masy
(ρ = const). Rozważane figury reprezentują zazwyczaj przekroje prętów. Dlatego zamiast określenia „figura płaska” stosuje się również określenie „przekrój”.
Definicje poszczególnych parametrów geometrycznych figur płaskich wymagają wprowadzenia prostokątnego układu osi współrzędnych x, y (rys. 22.1).
Rys. 22.1
Rys. 22.2
Pole przekroju
∫
A = dA > 0 [m2 ].
(22.1)
A
Momenty statyczne przekroju:
− względem osi x
Sx =
∫ ydA
[ m3 ],
(22.2a)
∫ xdA
[ m3 ].
(22.2b)
A
− względem osi y
Sy =
A
Momenty bezwładności:
− względem osi x
Jx =
∫ y dA > 0
[ m4 ],
(22.3a)
∫ x dA > 0
[ m4 ],
(22.3b)
2
A
− względem osi y
Jy =
2
A
− odśrodkowy (dewiacyjny)
J xy =
∫ x dA
2
[ m4 ].
(22.3c)
A
Z podanych wyżej wzorów definicyjnych wynika, że momenty statyczne mierzymy w jednostkach
3
3
długości do potęgi trzeciej (np. [m ], [cm ]). Mogą one przyjmować wartości dodatnie lub ujemne. Mo4
4
menty bezwładności mierzymy w jednostkach długości do potęgi czwartej (np. [m ], [cm ]). Osiowe
momenty bezwładności przybierają zawsze wartości dodatnie i są pewną miarą rozproszenia pola figury
względem danej osi. Im rozproszenie jest większe, tym osiowy moment bezwładności jest większy. Moment dewiacyjny może być zarówno dodatni, jak i ujemny, a jego wartość bezwzględna jest miarą asymeAndrzej Gawęcki - „Mechanika materiałów i konstrukcji prętowych” 2003r.
Alma Mater
Dodatek
2
trii figury względem przyjętego układu współrzędnych. Łatwo zauważyć, że jeśli choć jedna z osi układu
jest osią symetrii figury, to moment dewiacyjny względem tego układu jest równy zeru (por. rys. 22.2).
Wynika to stąd, że iloczyny xydA w odpowiadających sobie punktach wzajemnie się znoszą.
22.2. OSIE ŚRODKOWE, ŚRODEK CIĘŻKOŚCI
Oś środkowa to taka oś, względem której moment statyczny jest równy zeru. Środek ciężkości (SC) to
punkt przecięcia osi środkowych.
Rys. 22.3
Rys. 22.4
Jeśli osie x0 i y0 są osiami środkowymi, to
S x0 =
(a)
∫ y0 dA = ∫ ( y − yc )dA = 0,
A
S y0 =
(b)
A
∫ x0 dA = ∫ ( x − xc )dA = 0.
A
A
Po rozpisaniu zależności (a) i (b) otrzymujemy:
S x0 =
∫ ydA − yc ∫ dA = S x − yc ⋅ A = 0,
A
S y0 =
A
∫ xdA − xc ∫ dA = S y − xc ⋅ A = 0,
A
A
skąd wyznaczamy współrzędne środka ciężkości xc i yc :
Sy
S
xc =
,
yc = x .
A
A
(22.4)
Jeśli znamy położenie środka ciężkości i pole figury, to momenty statyczne tej figury względem osi x, y
leżących w odległościach xc i yc obliczamy wprost z równań (22.4):
S x = A ⋅ yc ,
S y = A ⋅ xc .
Jeśli figura składa się z n części o znanych polach Ai oraz współrzędnych środków ciężkości
xi i yi (i = 1 ,2 ,..., n) , to (por. rys. 22.4):
n
Sx =
∑
i =1
n
S xi =
∑
n
Ai ⋅ yi ;
Sy =
i =1
Andrzej Gawęcki - „Mechanika materiałów i konstrukcji prętowych” 2003r.
∑
i =1
n
S yi =
∑ Ai ⋅ xi .
(22.5)
i =1
Alma Mater
Dodatek
n
n
xc =
Sy
A
∑
3
Ai xi
= i =1
n
∑ Ai
∑ Ai yi
S
; yc = x = i =1
n
A
.
(22.6)
∑ Ai
i =1
i =1
22.3. MOMENTY BEZWŁADNOŚCI PRZY PRZESUNIĘCIU
I OBROCIE UKŁADU OSI WSPÓŁRZĘDNYCH.
KIERUNKI I WARTOŚCI GŁÓWNE
Założymy, że znamy wartości momentów bezwładności Jx', Jy', Jx'y' odniesione do układu osi x' i y'.
Dokonajmy przesunięcia równoległego układu osi z położenia x', y' do nowego położenia x, y. Pytamy
teraz, jakie wartości przyjmą momenty bezwładności Jx, Jy, Jxy odniesione do układu osi x, y, jeśli współrzędne przesunięcia względnego obu układów wynoszą xp i yp (rys. 22.5). Przesunięcie układów opisują
równania:
 x = x '+ x p ,

 y = y '+ y p .
(a)
Po podstawieniu tych zależności do wzorów definicyjnych (22.3) otrzymujemy:
(b)

Jx = y2dA = ( y'+ y p )2 dA = y'2 dA + 2 y p y' dA + y2p dA,

A
A
A
A
A


2
2
2
2
J y = x dA = ( x'+x p ) dA = x' dA + 2x p x' dA + x p dA,

A
A
A
A
A

Jxy = xydA = ( x'+x p ) ⋅ ( y'+ y p )dA = x' y' dA + x p y' dA + y p x' dA + x p y p dA.

A
A
A
A
A
A

∫
∫
∫
∫
∫
∫
∫
∫
∫
∫
∫
∫
∫
Rys. 22.5
∫
∫
∫
Rys. 22.6
Prawe strony równań (b) można przedstawić za pomocą parametrów geometrycznych figury związanych
z układem x', y' wykorzystując wzory (22.1), (22.2)
i (22.3):
 J x = J x ' + 2 y p ⋅ S x ' + y 2p ⋅ A,


2
(c)
 J y = J y ' + 2 x p ⋅ S y ' + x p ⋅ A,

 J xy = J x ' y ' + x p S x ' + y p ⋅ S y ' + x p ⋅ y p ⋅ A.
Alma Mater
Dodatek
4
Jeśli układ osi x', y' jest układem osi środkowych ( x ' = x 0 , y ' = y0 , x p = x c , y p = yc ), to wzory (c)
znacznie się uproszczą. Dla osi środkowych momenty statyczne S x ' = S xo = 0 i S y ' = S yo = 0, a równania (c) przyjmą postać:



J y = J y 0 + xc2 A,


J xy = J x 0 y 0 + xc yc A.

J x = J x 0 + yc2 A,
(22.7)
Są to tzw. wzory Steinera, bardzo użyteczne w obliczeniach.
Rozważymy teraz, jak zmieniają się momenty bezwładności przy obrocie układu osi współrzędnych.
Przyjmiemy, że znane są wartości Jx, Jy, Jxy w układzie osi x, y. Poszukujemy Jx', Jy', i Jx'y' w układzie osi
x', y' obróconym o kąt ϕ względem układu x y (rys. 22.6). Współrzędne punktów obu układów są powiązane wzorami transformacyjnymi:
 x ' = x cosϕ + y sin ϕ ,

 y ' = − x sin ϕ + y cosϕ .
(d)
W celu wyprowadzenia poszukiwanych zależności skorzystamy ze wzoru na zamianę zmiennych w całce
podwójnej:
∫ f ( x', y')dA' = ∫ f [ x'( x, y), y'( x, y)]J ⋅ dA,
(e)
A
A
gdzie jakobian
∂x '
∂x
J=
∂y '
∂x
∂x '
cosϕ sin ϕ
∂y
=
= 1.
∂y ' − sin ϕ cosϕ
∂y
Po podstawieniu wzorów transformacyjnych (d) do wzorów definicyjnych otrzymujemy:
 J = y '2 dA' = ( − x sin ϕ + y cosϕ ) 2 dA =
 x'
A'
A


2
2
2
2
 = sin ϕ x dA − 2 sin ϕ cosϕ xy dA + cos ϕ y dA,

A
A
A

2
2
 J y ' = x ' dA' = ( x cosϕ + y sin ϕ ) dA =

A'
A


= cos2 ϕ x 2 dA + 2 sin ϕ cosϕ xy dA + sin 2 ϕ y 2 dA,

A
A
A

 J = x ' y ' dA' = ( x cosϕ + y sin ϕ )( − x sin ϕ + y cosϕ ) 2 dA =
 xy ''
A'
A


= − sin ϕ cosϕ x 2 dA + sin ϕ cosϕ y 2 dA + (cos2 ϕ − sin 2 ϕ xydA.


A
A
A
∫
∫
∫
∫
(f)
∫
∫
∫
∫
∫
∫
∫
∫
∫
∫
∫
Prawe strony równań (f) można wyrazić za pomocą momentów bezwładności związanych z układem osi
x, y. Wygodnie też będzie wprowadzić funkcję trygonometryczne kąta 2ϕ:
sin 2 ϕ = 21 (1 − cos 2ϕ );
cos2 ϕ = 21 (1 + cos 2ϕ );
2 sin ϕ cosϕ = sin 2ϕ .
Ostatecznie poszukiwane wzory transformacyjne dla momentów bezwładności przy obrocie układu przyjmują postać:
Alma Mater
Dodatek
Jx + J y
Jx − J y

⋅ cos 2ϕ − J xy sin 2ϕ , 
2
2

Jx + J y Jx − J y

−
⋅ cos 2ϕ + J xy sin 2ϕ ,
J y' =
2
2

Jx − J y

J x' y' =
sin 2ϕ + J xy cos 2ϕ .

2

J x' =
+
5
(22.8)
Rzut oka na wzory (22.8) pozwala stwierdzić, że po obrocie układu suma osiowych momentów bezwładności nie ulega zmianie. Suma ta określa tzw. biegunowy moment bezwładności Jb. Moment ten jest
więc niezmiennikiem:
∫
J b = ( x 2 + y 2 )dA = J x + J y = J x ' + J y ' = const.
(22.9)
A
Szczegółowa analiza wzoru (22.8) prowadzi do wniosku, że niezmiennikiem jest również wyrażenie:
2
(22.10)
I3 = J x J y − J xy
= J x ' ⋅ J y ' − J x2' y ' = const.
W punkcie 22.1 zwróciliśmy uwagę na to, że jeśli jedna z osi układu jest osią symetrii figury, to moment dewiacyjny w tym układzie jest równy zeru. Powstaje pytanie, czy dla dowolnego niesymetrycznego przekroju jest również taki układ osi, w którym znika moment dewiacyjny. Wymaganie, by Jx'y' = 0,
stosownie do wzoru (22.8)3, nakłada na kąt ϕ = ϕ0 warunek:
Jx − Jy
⋅ sin 2ϕ 0 + J xy cos 2ϕ 0 = 0,
2
(g)
skąd
tg2ϕ 0 = −
2 J xy
Jx − J y
.
(22.11)
Zwróćmy uwagę, że do identycznego warunku z warunkiem (g) dochodzimy, poszukując ekstremalnych wartości osiowych momentów bezwładności jako funkcji kąta ϕ:
dJ y '
dϕ
=−
Jx − Jy
dJ x '
= 2⋅
⋅ sin 2ϕ + 2 ⋅ J xy cos 2ϕ = 0.
2
dϕ
Z powyższych rozważań wnioskujemy, że jest pewien wyróżniony układ osi współrzędnych, określony kątem ϕ0, dla którego osiowe momenty bezwładności osiągają wartości ekstremalne, a moment dewiacyjny znika. Taki układ osi nazywamy układem głównych osi bezwładności (I, II), a momenty osiowe
w tym układzie − głównymi momentami bezwładności. Wartości głównych momentów bezwładności
obliczamy po wstawieniu kąta ϕ0 z równania (22.11) do równań (22.8)1 i (22.8)2:

2
Jx + J y
 Jx − Jy 
2 
J max = J I =
+ 
 + J xy ,

2
2 


(22.12)
 ...
2

Jx + Jy
 Jx − J y 
2
J min = J II =
− 
 + J xy .
2
2 


Położenie osi I związanej z momentem JI określa się następująco:
− jeśli Jx > Jy , to ϕ0 jest kątem pomiędzy osią x a osią I,
− jeśli Jx < Jy , to ϕ0 jest kątem pomiędzy osią y a osią I.
Najczęściej obliczenia wykonujemy w układzie osi środkowych x0, y0. Wówczas osie I i II nazywamy
głównymi środkowymi osiami bezwładności, a momenty JI i JII − głównymi środkowymi momentami
bezwładności.
Alma Mater
Dodatek
6
Uważny czytelnik stwierdzi uderzającą analogię między wzorami (22.8)÷(22.11) a zależnościami występującymi w analizie płaskiego stanu naprężenia (p. 1.8). Jeśli we wzorach (22.8) przyjmiemy, że:
J x = σ x , J y = σ y , J xy = τ xy , J x ' = σ x ' , J y ' = σ y ' ,
J x' y' = τ x' y' ,
to otrzymamy zależności identyczne z wzorami transformacyjnymi (1.33) dla płaskiego stanu naprężenia.
Analogia ta wynika stąd, że momenty bezwładności tworzą płaski tensor drugiego rzędu. Wyjaśnienie
tensorowego charakteru momentów bezwładności zamieszczono w p. 22.4.
Wobec powyższego koło Mohra, omówione szczegółowo w rozdziale 1. (p. 1.8), jest również ilustracją graficzną wzorów transformacyjnych (22.8). Dla jasności trzeba też dodać, że konstrukcję koła wykonuje się, przyjmując że Jyx = −Jxy ! Ciekawostką jest, że Mohr w 1887 roku obmyślił konstrukcję koła
właśnie dla momentów bezwładności.
22.4. PARAMETRY GEOMETRYCZNE PRZEKROJU
JAKO WIELKOŚCI TENSOROWE
Momenty statyczne nazywają się często momentami pierwszego rzędu (stopnia), a momenty bezwładności − momentami rzędu rzędu (stopnia). Określenia te wynikają z potęg, w których występują współrzędne x, y we wzorach (22.2) i (22.3). Pole przekroju można by nazwać momentem rzędu zero. Nadmieniamy o tym nieprzypadkowo, gdyż pole przekroju, momenty statyczne i momenty bezwładności mają
własności tensorów odpowiednio rzędu zerowego, pierwszego i drugiego. Pole przekroju jest skalarem,
momenty statyczne Sx i Sy są współrzędnymi wektora, a momenty bezwładności Jx, Jy, Jxy − współrzędnymi tensora dwuwymiarowego.
Dla potwierdzenia powyższych uwag wyprowadzimy prawa transformacji momentów statycznych i
momentów bezwładności dla obrotu układu współrzędnych. Przyjmiemy najpierw następujące oznaczenia:
(a)
 x1 = x , x2 = y; x1' = x ' , x2' = y ' ;
M = S , M = S ; B = J , B = J , B = B = J
y
2
x
11
y 22
x 12
21
xy
 1
Wówczas wzory definicyjne (22.2) i (22.3) można zapisać następująco:
Mα =
(b)
∫ xα dA ,
A
Bαβ =
(c)
∫ xα xβ dA , (α , β = 1, 2),
A
a wzory transformacyjne współrzędnych punktów w konwencji sumacyjnej określają znane zależności
(por. rozdz. 1.):
xγ ' = xα ⋅ aαγ '
(d)
lub
(α , β = 1, 2; γ ', δ ' = 1', 2').
xδ ' = xβ ⋅ aβδ '
(e)
W układzie osi obróconych, stosownie do definicji (b) i (c) oraz wzorów (d) i (e), możemy napisać:
Mγ ' =
∫ xγ ' dA' = ∫ xα ⋅ aαγ ' dA = aαγ ' ∫ xα dA,
A'
Bγ 'δ ' =
A
A
∫ xγ ' ⋅ xδ 'dA' = ∫ xα aαγ ' ⋅ xβ aβδ 'dA = aαγ 'aβδ ' ∫ xα ⋅ xβ dA,
A'
A
A
skąd
(f)
 Mγ ' = Mα ⋅ aαγ ' ,

 Bγ 'δ ' = Bαβ ⋅ aαγ ' ⋅ aβδ ' .
Alma Mater
Dodatek
7
Wzory (f) definiują transformację wektora i tensora przy obrocie układu współrzędnych w przestrzeni
dwuwymiarowej, co wykazuje, że rzeczywiście momenty statyczne są współrzędnymi wektora, a momenty bezwładności − współrzędnymi tensora. Podobnie jest i w przestrzeni trójwymiarowej, gdzie momenty
bezwładności tworzą dziewięć współrzędnych tensora symetrycznego, zdefiniowanych następująco
(Karaśkiewicz [24]):


(g)
Bij = B ji =  xk xk ⋅ dV  ⋅ δij − xi x j ⋅ dV ; (i , j = 1, 2, 3).


V
V

∫
∫
Tensor bezwładności figury płaskiej jest reprezentowany przez macierz:
Jy
J=
 J yx
(h)
J xy 
.
J x 
Z postaci tej wnioskujemy, że niezmienniki tensora bezwładności są opisane wzorami (por. również wzory (22.9) i (22.10)):
(i)
I1 = I 2 = Jb = J x + J y = J x ' + J y ' = J I + J II = const > 0,
(j)
I3 =
Jy
J xy
J yx
Jx
2
= J y ⋅ J x − J xy
= J y ' J x ' − J x2' y ' = JI ⋅ JII = const > 0.
22.5. WSKAZÓWKI PRAKTYCZNE
Analogia między momentami bezwładności a płaskim stanem naprężenia nie jest jednak pełna. Istotna
różnica polega na tym, że osiowe momenty bezwładności są zawsze dodatnie, podczas gdy naprężenia
normalne mogą być również ujemne. Okoliczność ta nakłada pewne warunki na wartość momentów bezwładności. Ponieważ I 3 = J I ⋅ J II > 0 , więc zgodnie ze wzorem (j) w p. 22.4 musi zachodzić nierówność:
2
J x ⋅ J y − J xy
> 0,
skąd
(a)
J xy < J x ⋅ J y .
Z nierówności ( x − y )2 = x 2 + y 2 − 2 xy > 0 wynika dalej, że
J x + J y − 2 J xy > 0 ,
skąd
(b)
J xy <
Jx + J y
2
.
Ze wzoru (a) wynika, że wartość bezwzględna momentu dewiacyjnego musi być mniejsza od średniej
geometrycznej osiowych momentów bezwładności. Ze wzoru (b) wynika natomiast, że moment dewiacyjny musi być mniejszy od średniej arytmetycznej osiowych momentów bezwładności. Ponieważ średnia geometryczna nigdy nie jest większa od średniej arytmetycznej, zatem miarodajna jest nierówność
(a), którą można zapisać następująco:
− J x ⋅ J y < J xy <
Jx ⋅ J y .
(22.13)
Nierówność (22.13) dowodzi, że dowolna trójka liczb nie tworzy tensora bezwładności. Nierówność ta −
słuszna również dla dowolnego, nieśrodkowego układu współrzędnych − jest właściwie jedynym sposobem kontroli ilościowej obliczonych wartości Jx, Jy, Jxy .
Gdy korzysta się z gotowych wzorów lub tablic należy ustalić właściwy znak momentu dewiacyjnego.
Najczęściej zdarza się to w przekrojach trójkątnych lub kątownikach. O znaku Jxy decyduje położenie
ramion kątownika (lub trójkąta). Rozróżniamy tu 4 przypadki przedstawione na rys. 22.7.
Alma Mater
Dodatek
8
Rys. 22.7
W tablicy IV podano parametry geometryczne najczęściej spotykanych figur płaskich.
Tablica IV
22.6. PRZYKŁAD LICZBOWY
Dany jest przekrój złożony, przedstawiony na rys. 22.8.
Obliczyć:
a) położenie środka ciężkości,
b) momenty bezwładności względem osi środkowych x 0 , y 0 ,
c) kierunki środkowych osi głównych,
d) główne środkowe momenty bezwładności,
e) momenty bezwładności względem osi środkowych x 0' , y 0' , obróconych względem osi x 0 , y 0 o kąt
ϕ = −40°.
Obliczenia zilustrować kołem Mohra.
Alma Mater
Dodatek
9
Rys.22.8
Rozwiązanie
Przekrój składa się z czterech elementów. Dla kształtowników walcowanych (elementy 1, 3 i 4) odczytano z tablic:
Element 1. L120×80×10
A = 19,2 cm2 , e y = 1,96 cm, ex = 3,93 cm,
tgϕ 0 = 0,436, J min = 57,7 cm4 , J x = 279 cm4 , J y = 99,6 cm4 .
Element 3. L100×100×8
A = 15,5 cm2 , e y = ex = 2,74 cm,
J min = 59,9 cm4 , J max = 230 cm4 , J x = J y = 145 cm4 .
Element 4.[ 200
A = 32,2 cm2 , e = 2,01 cm, J x = 1910 cm4 , J y = 148 cm4 .
Zasadnicze obliczenia odniesiono do pomocniczego układu współrzędnych x, y
(por. rys. 22.8).
a) Obliczenie współrzędnych środka ciężkości całego przekroju
Obliczenie wykonamy według wzorów (22.6):
(a)
xc =
∑ Ai xi ,
∑ Ai
yc =
∑ Ai yi .
∑ Ai
Współrzędne x1, y1 obliczamy ze wzorów na obrót układu:
(b)
x1 = x '1 cos ϕ + y '1 sin ϕ ,
y1 = − x '1 sin ϕ + y '1 cos ϕ ,
gdzie ϕ = −α = −arctg(20 / 15) = 53,13o jest kątem obrotu układu x', y' względem układu x, y (kierunek
obrotu układu x', y' przy przejściu do układu x, y jest zgodny
z ruchem wskazówek zegara i stąd znak minus). Obliczenie pozostałych wartości
xi, yi nie wymaga komentarzy.
Alma Mater
Dodatek
10
Element 1
sin ϕ = sin( −53,13o ) = −0,80;
cosϕ = cos( −53,13o ) = 0,60,
x '1 = 8 − 1,96 = 6,04 cm, y '1 = 3,93 + 1,0 = 4,93 cm,
x1 = 6,04 ⋅ 0,60 + 4,93 ⋅ ( −0,80) = −0,32 cm,
y1 = −6,04 ⋅ ( −0,80) + 4,93 ⋅ 0,60 = 7,70 cm.
Element 2
x2 = 7,50 cm,
y2 = 10,00 cm.
Element 3
x3 = 15,00 + 2,00 + 10,00 − 2,74 = 24,26 cm,
y3 = 20,00 − 2,74 = 17,26 cm.
Element 3
x4 = 15,00 + 2,00 + 10,00 + 2,01 = 29,01 cm,
y4 = 10,00 cm.
Tablica V
Sumowania występujące we wzorach (a) wykonano w tablicy V. Współrzędne środka ciężkości całej
figury ( A = 116,9 cm2 , S y = 1679,0 cm3 , S x = 1239,1 cm3 ):
xc =
1679,0
= 14,36 cm,
116,9
yc =
1239,1
= 10,60 cm.
116,9
Zwróćmy uwagę na to, że środek ciężkości całego przekroju musi leżeć w obrębie wieloboku utworzonego przez połączenie środków ciężkości figur składowych.
W naszym zadaniu wymaganie to jest spełnione (por. rys. 22.8).
b) Obliczenie momentów bezwładności względem osi środkowych x 0 , y 0
Współrzędne środków ciężkości w układzie osi środkowych dla poszczególnych figur składowych
obliczamy ze wzorów:
(c)



xci = xi − xc ,
yci = yi − yc .
Momenty bezwładności względem osi środkowych wyznaczamy na podstawie wzorów Steinera:
Alma Mater
Dodatek
∑(Jx
) ∑ J + ∑ A (y − y ) ,
= ∑ ( J + A ⋅ x ) = ∑ J + ∑ A (x − x ) ,
J x0 =
2
+ Ai ⋅ yci
=
0i
i
(d)
J y0
11
i
i
y 0i
i
∑(Jx
y 0i
i
i
c
i
i
i
) ∑ Jx
+ Ai ⋅ xci yci =
0i y0i
i
2
i
2
ci
i
J x0 y0 =
x0i
0i y0i
+
i
c
2
∑ Ai (xi − xc ) ⋅ ( yi − y y ).
i
Wyznaczenie momentów bezwładności poszczególnych figur względem własnych osi środkowych,
równoległych do osi x0 i y0 , tzn. J x0i , J y0i , J x0i y0i , wymaga pewnych dodatkowych obliczeń.
Element 1
Najpierw trzeba ustalić momenty bezwładności dla osi x01 i y01 . Na podstawie tablic otrzymujemy:
J x01 = 279 cm4 ,
J y01 = 99,6 cm4 .
Moment dewiacyjny J x01 y01 można wyznaczyć kilkoma sposobami, ponieważ znamy zarówno
J min = JII , jak i tgϕ0 .
Sposób 1. Ponieważ JI + JII = J x01' + J y01' ,
J I = J x01' + J y01' − J II = 279,0 + 99,6 − 57,7 = 320,9 cm4 .
więc :
Ze wzoru (22.10) na obliczenie niezmiennika I3 otrzymujemy:
J x01' J y01' − J x2 y = J I J II ,
01' 01'
skąd
J x01 ' y01 ' =
J x01 ' J y01 ' − J I JII = 279 ⋅ 99,6 − 320,9 ⋅ 57,7 = 96,3 cm4 > 0,
bo w układzie osi x ' 01 , y ' 01 kątownik jest w położeniu dodatnim.
Sposób 2. Ze wzoru na obliczenie tg2ϕ0 mamy ( 2ϕ0 = 2arctg(0,436) = 47,11o ):
J x ' − J y01 '
279 − 99,6
J x01 ' y01 ' =
⋅ tg2ϕ 0 ,
⋅ tg47,11° = 96,6 cm4 .
J x01 ' y01 ' = 01
2
2
Sposób 3. Ze wzoru transformacyjnego na Jxy, wyrażonego przez główne momenty bezwładności
J I i J II , mamy:
320,9 − 57,7
J − JII
J x01 ' y01 ' = I
⋅ sin 2ϕ =
⋅ sin 47,11° = 96,4 cm4 .
2
2
J x01 ' y01 ' = 96,5 cm4 . W celu obliczenia J x01 , J y01 , J x01 y01
wykorzystamy wzory transformacyjne na obrót układu z położenia x ' 01 , y ' 01 do położenia x01, y01 o kąt
α = −53,13°.
Do dalszych obliczeń przyjmujemy, że
J x01 =
279 + 99,6 279 − 99,6
cos( −2 ⋅ 53,13° ) − 96,5 ⋅ sin( −2 ⋅ 53,13° ) = 256,8 cm4 ,
+
2
2
J y01 = 279 + 99.6 − 256,8 = 121,8 cm4 ,
J x01 y01 =
279 − 99,6
sin( −2 ⋅ 53,13° ) + 96,5 ⋅ cos( −2 ⋅ 53,13° ) = −113,1 cm4 .
2
Element 2 (blacha 250 mm×20 mm)
Momenty bezwładności względem osi x02' i y02'
Alma Mater
Dodatek
12
25,0 ⋅ 2,03
2,0 ⋅ 25,03
= 16,7 cm4 ; J y02 ' =
= 2604,2 cm4 .
12
12
Ponieważ osie x ' 02 , y ' 02 są głównymi osiami bezwładności, więc J x02 ' y02 ' = 0. Momenty bezwładności
względem osi środkowych x02 i y02 obliczymy podobnie jak dla elementu 1:
J x02 ' =
J x02 =
16,7 + 2604,2 16,7 − 2604,2
+
⋅ cos( −2 ⋅ 53,13° ) = 1672,7 cm4 ,
2
2
J y02 = 16,7 + 2604,2 − 1672,7 = 948,2 cm4 ,
J x02 y02 =
16,7 − 2604,2
sin( −2 ⋅ 53,13° ) = 1242,0 cm4 .
2
Element 3
J x03 = J y03 = 145 cm 4 .
Moment dewiacyjny J x 03 y 03 obliczymy ze wzorów transformacyjnych wiedząc, że główne osie
bezwładności są pochylone pod kątem −45° w stosunku do osi
i J II = 60 cm 4
J x03 y03 =
x 03 , y 03 , a J I = 230 cm 4
230,0 − 66,0
sin( −2 ⋅ 45° ) = −85,0 cm4 .
2
Element 4
Osie x04 i y04 są głównymi osiami bezwładności ceownika. Mamy więc:
J x04 = 1910 cm 4 ,
J y04 = 148 cm 4 ,
J x04 y04 = 0.
Dalsze obliczenia według wzorów (d) zamieszczono w tablicy. Momenty bezwładności całego przekroju
względem osi środkowych x0 , y0 wynoszą więc:
J x0 =
∑ J x + ∑ Ai ( yi − yc )2 = 3984,5 + 868,7 = 4853,2 cm4 ,
0i
i
J y0 =
i
∑ J y + ∑ Ai ( xi − xc )2 = 1363,0 + 14920,6 = 16283,6 cm4 ,
0i
i
J x0 y0 =
∑ Jx
i
i
0i y0i
+
∑ Ai ( xi − xc )( yi − yc ) = 1043,9 + 1736,8 = 2780,7 cm4 .
i
Sprawdzenie poprawności uzyskanych rezultatów jest w ogólności niemożliwe. Jednak w celu
wychwycenia oczywistych błędów warto zdać się na intuicję oraz sprawdzić nierówności (22.13). W
naszym zadaniu przekrój jest rozbudowany wzdłuż osi x0, jest więc intuicyjnie oczywiste, że moment
bezwładności J y0 musi być wyraźnie większy od momentu bezwładności J x 0 . Można też oszacować
„na oko” znak momentu dewiacyjnego, rozpatrując rozmieszczenie materiału w poszczególnych
ćwiartkach układu x0, y0. Na rysunku 22.8 widać, że większa część materiału jest rozmieszczona w
ćwiartkach I i III (ćwiartki dodatnie), a więc moment dewiacyjny J x 0 y 0 powinien być większy od zera.
Tak wiec przesłanki intuicyjne potwierdzają poprawność uzyskanych wyników. Również nierówności (a)
i (b) z p. 22.5 są spełnione:
J xy = 2780,7 cm4 < 4853,2 ⋅ 16283,6 = 8890,56 cm4 ,
J xy = 2780,7 cm4 <
4853,2 + 16283,6
= 10568,4 cm4 .
2
Powyższa krytyczna ocena uzyskanych rezultatów jest konieczna, gdyż − jak wykazuje doświadczenie
− największe błędy popełniamy właśnie podczas obliczania wyjściowych wartości momentów bezwładności.
Alma Mater
Dodatek
13
c) Obliczenie kierunków środkowych osi głównych
Położenie środkowych osi głównych I i II jest określone przez kąt ϕ0:
tg2ϕ 0 = −
2 J x0 y0
J x 0 − J y0
=−
2 ⋅ 2780,7
= 0,4865,
4853,2 − 16283,6
skąd ϕ 0 =
25,94°
= 12,97° .Ponieważ J x0 < J y0 ,
2
więc kąt ϕ0 jest kątem między osią x0 a osią II.
d) Obliczenie głównych środkowych momentów bezwładności
2
JI =
4853,2 + 16283,6
 4853,2 − 16283,6 
2
4
+ 
 + 2780,7 = 16924,2cm ,


2
2
J II =
4853,2 + 16283,6
 4853,2 − 16283,6 
2
4
− 
 + 2780,7 = 4212,6 cm .


2
2
2
Sprawdzimy jeszcze wartość niezmiennika I3:
I 3 = J I ⋅ J II = 16924,2 ⋅ 4212,6 = 7,129 ⋅ 107 cm8 = J x0 ⋅ J y0 − J x y 2 .
0 0
e) Obliczenie momentów bezwładności względem osi x ' 0 , y ' 0 , obróconych względem osi x 0 , y 0 o
kąt ϕ = −40°.
Do obliczenia wykorzystujemy wzory transformacyjne:
J x0 ' =
4853,2 + 16283,6 4853,2 − 16283,6
+
cos(−80° ) − 2780,7 sin(−80° ) = 12314,4 cm4 ,
2
2
J y0 ' = 4853,2 + 16283,6 − 12314,4 = 8822,4 cm4 ,
J x0 ' y0 ' =
4853,2 − 16283,6
⋅ sin(−80° ) + 2780,7 ⋅ cos(−80° ) = 6111,2 cm4 .
2
Sprawdzenie I3:
I 3 = 12314,4 ⋅ 8822,4 − 6111,2 2 = 7,129 ⋅ 107 cm8 .
Rezultaty obliczeń zawartych w punktach c), d) i e) sprawdzono za pomocą koła Mohra (rys. 22.9). Z
rysunku odczytano (w nawiasach podano wartości ścisłe):
ϕ 0 = 13o
(12,97 o ),
JI = 16940 cm4
(16924,2 cm4 ),
JII = 4200 cm4
(4212,6 cm4 ),
J x0 ' = 12390 cm4
(12314,4 cm4 ),
J y0 ' = 8780 cm4
(8822,4 cm4 ),
J x0 ' y0 ' = 6110 cm4
( 6111,2 cm4 ).
Alma Mater
Dodatek
14
Rys. 22.9
Alma Mater

22. parametry geometryczne figur płaskich

Transkrypt

Podobne dokumenty

przekrój

Ćwiczenie 2

Zadania typu 1 – „łamigłówka”. Dany jest moment bezwładności

Wyznaczyć główne, centralne momenty bezwładności powierzchni

Zestawienie elementów usługi zamierzone powierzyć

Dane samochodu ford transit

Charakterystyki geometryczne figur płaskich

VL - UWM

Wyznaczyć główne, centralne momenty bezwładności powierzchni

Wytrzymałość materiałów II ZAD 1 (wyniki)by Tommy