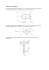Płaska geometria mas - przykładowe zadanie

POLITECHNIKA ŚLĄSKA. WYDZIAŁ ORGANIZACJI I ZARZĄDZANIA.
Katedra Podstaw Systemów Technicznych
-
Mechanika Stosowana –
____________________________________________________________________
Płaska geometria mas
2c
2c
3c
Dla zadanego pola przekroju wyznaczyć:
- połoŜenie środka cięŜkości S(xs, ys)
- momenty bezwładności (JxS, JyS) i dewiacji (JXsyS) względem osi xs, ys
(centralnych)
główne centralne osie (1, 2) oraz momenty bezwładności (J1, J2).
Dane: C= 2 [cm]
1. Środek cięŜkości
y
P1
Śr1(x1,y1)
4c
Śr2(x2,y2)
P2
2c
o
--- PŁASKA GEOMETRIA MAS ---
x
1
POLITECHNIKA ŚLĄSKA. WYDZIAŁ ORGANIZACJI I ZARZĄDZANIA.
Katedra Podstaw Systemów Technicznych
Mechanika Stosowana –
-
____________________________________________________________________
W pierwszej kolejności naleŜy przyjąć układ osi współrzędnych xy. W podanym
przykładzie oś pionowa oy stanowi oś symetrii przekroju.
Następnie naleŜy podzielić pole przekroju na figury proste i wyznaczyć dla tych
figur środki cięŜkości oraz pola powierzchni.
PowyŜsze pole przekroju da się podzielić na 2 figury: kwadrat i trójkąt.
Pola powierzchni wynoszą:
P = 4c
1
P = 2 2c * 3c = 3c
2
1
2
2
Środek cięŜkości kwadratu znajduje się w punkcie przecięcia przekątnych. Jego odległość
od osi X wynosi:4c = 3c (wysokość trójkąta) + 1c (połowa wysokości kwadratu).
Środek cięŜkości trójkąta znajduje się w 2/3 wysokości (Tablica 7.1 na stronie 222 ksiąŜki
”Metodyczny zbiór zadań z mechaniki”), stąd 2/3*3c = 2c.
Współrzędne środków cięŜkości figur składowych przekroju są następujące:
- dla kwadratu: (0, 4c)
- dla trójkąta: (0, 2c)
Współrzędne środka cięŜkości całego przekroju naleŜy wyznaczyć ze wzorów (1):
∑ (S x )
n
xs =
i
i =1
i =1
Gdzie:
y
n
∑S
∑ (S y )
n
i
i
s
=
i
i =1
i
n
∑S
i =1
(1)
i
Si - to pole i-tej figury wchodzącej w skład przekroju,
xi, yi – współrzędne środka cięŜkości i-tej figury.
Korzystając ze wzorów (1) wyznaczamy środek cięŜkości przekroju S0:
Współrzędna x środka cięŜkości znajduje się na osi symetrii przekroju – x0 = 0.
*
+
*
y = 4c 4c 3c 2c = 3,15c
4c + 3c
2
Współrzędna y0:
0
2
2
2
Współrzędne środka cięŜkości badanego przekroju: Śr0= (0; 3,15c).
W punkcie środka cięŜkości zaczepiony jest układ osi centralnych xs, ys.
--- PŁASKA GEOMETRIA MAS ---
2
POLITECHNIKA ŚLĄSKA. WYDZIAŁ ORGANIZACJI I ZARZĄDZANIA.
Katedra Podstaw Systemów Technicznych
-
Mechanika Stosowana –
____________________________________________________________________
y
ys
Śr0(0; 3,15c)
xs
3,15c
o
x
2. Momenty bezwładności względem osi centralnych
Momenty bezwładności względem osi centralnych – przechodzących przez środek
cięŜkości - wyznaczane są ze wzorów Steinera:
J
=
J
xs
+a
2
x
S
J
=
J
ys
+b
2
y
S
Jxs oraz Jys – momenty bezwładności poszczególnych figur względem osi x i y. Wartości
momentów bezwładności dla podstawowych figur – znajdują się w tablicy 7.1 na stronie
222 ksiąŜki ”Metodyczny zbiór zadań z mechaniki”.
Jx= Jxs+a2*S
momenty bezwładności względem osi x
 (2c )4
  2c * (3c )3

2
2
2
2
=
+
(
4
c
−
3
,
15
c
)
*
4
c
+
+
(
2
c
−
3
,
15
)
*
3
c




J x 12
36

 

1
2
3
4
5
6
1. moment bezwładności kwadratu względem osi x
2. odległość składowej x środka cięŜkości kwadratu od składowej x środka cięŜkości
całego przekroju
3. pole powierzchni kwadratu
4. moment bezwładności trójkąta względem osi x
5. odległość składowej x środka cięŜkości trójkąta od składowej x środka cięŜkości
całego przekroju
6. pole powierzchni trójkąta
--- PŁASKA GEOMETRIA MAS ---
3
POLITECHNIKA ŚLĄSKA. WYDZIAŁ ORGANIZACJI I ZARZĄDZANIA.
Katedra Podstaw Systemów Technicznych
-
Mechanika Stosowana –
____________________________________________________________________
Jx = 1,33 c4 + 2,89 c4 + 1,5 c4 + 3,97 c4 = 9,69 c4
Jx = 9,69 * 24 = 155,04 cm4
Jy= Jys+b2*S
momenty bezwładności względem osi y
 (2c )4
  3c * (2c )3

2
2
+ (0 − 0) * 4c  + 
+ (0 − 0) 2 * 3c 2 
Jy = 
 12
  36

1
2
3
4
5
6
1. moment bezwładności kwadratu względem osi y
2. odległość składowej y środka cięŜkości kwadratu od składowej y środka cięŜkości
całego przekroju (odległość ta wynosi 0 – poniewaŜ oba środki cięŜkości leŜą na
osi symetrii)
3. pole powierzchni kwadratu
4. moment bezwładności trójkąta względem osi y
5. odległość składowej y środka cięŜkości trójkąta od składowej y środka cięŜkości
całego przekroju
6. pole powierzchni trójkąta
J
y
 16 c
= 
 12
4
24 c
+
36
4

 = 1 , 33 c

4
+ 0 , 67 c
4
= 2c
Jy = 2 * 24 = 32
3. Moment dewiacji (moment dewiacji względem obu osi)
JxSyS = Jx1y1+a1b1S1+ Jx2y2+a2b2S2
Jx1y1 – moment dewiacji kwadratu = 0
Jx2y2 – moment dewiacji trójkąta =
JxSyS = 0 + 0,7225c2 *0*4c2
−
J xy = −
(2c )2 (3c )2
72
b2h2
72
+ 1,32*0*3c2 = - 0,5 c4
JxSyS = - 0,5 * 24 = - 8
--- PŁASKA GEOMETRIA MAS ---
4
4
POLITECHNIKA ŚLĄSKA. WYDZIAŁ ORGANIZACJI I ZARZĄDZANIA.
Katedra Podstaw Systemów Technicznych
-
Mechanika Stosowana –
____________________________________________________________________
4. Główne osie centralne
Główne osie stanowią układ współrzędnych, względem których moment dewiacji danej
figury jest równy zero. Osie główne oznaczane są przez 1, 2.
Główne osie centralne obrócone są względem osi centralnych figury płaskiej o pewien
kąt, taki Ŝe:
tg2φ =
−
tg2φ =
−
2 J xy
Jx − Jy
2 * (−8)
16
=
= 0,1300
155,04 − 32 123,04
tgφ = 0650
Po odczytaniu z tablic wartości kąta otrzymujemy: φ = 3°40` - oznacza to, Ŝe główne
osie centralne obrócone są względem osi centralnych o kąt: φ = 3°40`.
2
y
ys
φ = 3°40`.
1
Śr0(0; 3,15c)
o
xs
x
5. Osiowe momenty bezwładności
Osiowe momenty bezwładności wyznaczone względem osi głównych (tzw. Główne
momenty bezwładności) mają wartości ekstremalne: moment względem jednej z nich
jest maksymalny, oznaczamy go przez J1, drugi – minimalny, oznaczamy go przez J2:
J 1 = J max =
J 2 = J max =
Jx + Jy
2
Jx + Jy
2
 Jx − Jy
+ 
 2

 + J xy 2

 J − Jy
−  x
 2

 + J xy 2

2
2
--- PŁASKA GEOMETRIA MAS ---
5
POLITECHNIKA ŚLĄSKA. WYDZIAŁ ORGANIZACJI I ZARZĄDZANIA.
Katedra Podstaw Systemów Technicznych
-
Mechanika Stosowana –
____________________________________________________________________
2
J 1 = J max
 9,69c 4 + 2c 4 
9,69c 4 + 2c 4
 + (−0,5) 2
=
+ 
2
2


J 1 = J max
 9,69c 4 + 2c 4
9,69c 4 + 2c 4
=
− 
2
2

2

 + (−0,5) 2

--- PŁASKA GEOMETRIA MAS ---
6