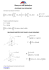(x, y) : x, y ∈ R

Funkcje dwóch i trzech zmiennych
Niech R2 = {(x, y) : x, y ∈ R} oznacza płaszczyznę,
R3 = {(x, y, z) : x, y, z ∈ R} przestrzeń.
Odległość punktów będziemy określali następująco:
|P1 P0 | =
|P1 P0 | =
q
(x1 − x0 )2 + (y1 − y0 )2 , P0 = (x0 , y0 ), P1 = (x1 , y1 ),
q
(x1 − x0 )2 + (y1 − y0 )2 + (z1 − z0 )2 , P0 = (x0 , y0 , z0 ), P1 = (x1 , y1 , z1 ).
Definicja 1 Otoczeniem o promieniu r > 0 punktu P0 na płaszczyźnie lub w przestrzeni
nazywamy zbiór
O(P0 , r) = {P : |P0 P | < r} .
Definicja 2 Zbiór jest otwarty, jeżeli każdy punkt tego zbioru jest zawarty w tym zbiorze
wraz z pewnym swoim otoczeniem
Definicja 3 Funkcją f dwóch zmiennych określoną na zbiorze A ⊂ R2 (R3 ) o wartościach
w R nazywamy przyporządkowanie każdemu punktowi ze zbioru A dokładnie jednej liczby
rzeczywistej.
z = f (x, y), (x, y) ∈ A
Zbiór A nazywamy dziedziną funkcji f i oznaczamy przez Df .
Definicja 4 Wykresem funkcji dwóch zmiennych nazywamy zbiór
{(x, y, f (x, y)) : (x, y) ∈ Df } .
Definicja 5 Poziomicą wykresu funkcji f , odpowiadającą poziomowi h ∈ R, nazywamy
zbiór
{(x, y) ∈ Df : f (x, y) = h} .
Niech f będzie określona na zbiorze otwartym D zawierającym punkt (x0 , y0 ).
Definicja 6 f jest ciągła w punkcie (x0 , y0 ), gdy
^ _
^
>0 δ>0 (x,y)∈D
q
[( (x − x0 )2 + (y − y0 )2 < δ) ⇒ (|f (x, y) − f (x0 , y0 )| < )]
Pochodne cząstkowe
Definicja 7 Pochodną cząstkową pierwszego rzędu funkcji f względem x w punkcie (x0 , y0 )
określamy wzorem
∂f
f (x0 + ∆x, y0 ) − f (x0 , y0 )
(x0 , y0 ) = lim
,
∆x→0
∂x
∆x
o ile ta granica istnieje.
Uwaga 1 Niech F (x) = f (x, y0 ). Wtedy
∂f
(x0 , y0 )
∂x
= F 0 (x0 ).
Analogicznie
∂f
f (x0 , y0 + ∆y) − f (x0 , y0 )
(x0 , y0 ) = lim
,
∆y→0
∂y
∆y
o ile ta granica istnieje.
Uwaga 2 Niech G(y) = f (x0 , y). Wtedy
∂f
(x0 , y0 )
∂y
= G0 (y0 ).
Definicja 8 Jeżeli f ma pochodne cząstkowe pierwszego rzędu w każdym punkcie zbioru
otwartego D ⊂ R2 , to funkcje
∂f
∂f
(x, y),
(x, y), gdzie (x, y) ∈ D
∂x
∂y
nazywamy pochodnymi cząstkowymi pierwszego rzędu f na zbiorze D.
Płaszczyzna styczna
Załóżmy, że pochodne cząstkowe ∂f
, ∂f są ciągłe w punkcie (x0 , y0 ). Wtedy płaszczyzna
∂x ∂y
o równaniu
∂f
∂f
(x0 , y0 )(x − x0 ) +
(x0 , y0 )(y − y0 ) + f (x0 , y0 )
z=
∂x
∂y
jest styczna do wykresu funkcji z = f (x, y) w punkcie (x0 , y0 , f (x0 , y0 )).
Pochodne cząstkowe wyższych rzędów
Niech f ma pochodne
∂f ∂f
,
∂x ∂y
na zbiorze otwartym D oraz niech (x0 , y0 ) ∈ D.
Definicja 9 Pochodne cząstkowe drugiego rzędu f w punkcie (x0 , y0 ) określamy wzorami:
∂ 2f
∂ ∂f
( )(x0 , y0 ) = fxx (x0 , y0 )
(x0 , y0 ) =
2
∂x
∂x ∂x
∂ 2f
∂ ∂f
(x0 , y0 ) =
( )(x0 , y0 ) = fxy (x0 , y0 )
∂x∂y
∂x ∂y
∂ 2f
∂ ∂f
(x0 , y0 ) =
( )(x0 , y0 ) = fyx (x0 , y0 )
∂y∂x
∂y ∂x
∂ 2f
∂ ∂f
( )(x0 , y0 ) = fyy (x0 , y0 )
(x0 , y0 ) =
2
∂y
∂y ∂y
Twierdzenie 1 (Schwartza o pochodnych mieszanych)
∂2f
∂2f
, ∂y∂x
istnieją na otoczeniu punktu (x0 , y0 ) oraz będą ciągłe
Niech pochodne cząstkowe ∂x∂y
w punkcie (x0 , y0 ). Wtedy
∂ 2f
∂ 2f
(x0 , y0 ) =
(x0 , y0 ).
∂x∂y
∂y∂x
Pochodna cząstkowa n-tego rzędu
∂ nf
(x0 , y0 ), gdzie k + l = n
∂y k ∂xl
-pochodna cząstkowa n-tego rzędu funkcji f w punkcie (x0 , y0 ) powstała w wyniku lkrotnego różniczkowania względem zmiennej x i następnie k-krotnego różniczkowania
względem zmiennej y
Pochodna kierunkowa funkcji
Niech ~v = (vx , vy ) będzie wersorem na płaszczyźnie. Niech f będzie określona na zbiorze
otwartym D ⊂ R2 oraz niech punkt (x0 , y0 ) ∈ D.
Definicja 10 Pochodną kierunkową funkcji f w punkcie (x0 , y0 ) w kierunku wersora ~v
określamy wzorem:
f (x0 + tvx , y0 + tvy ) − f (x0 , y0 )
∂f
(x0 , y0 ) = lim+
.
t→0
∂~v
t
Uwaga 3 Niech F (t) = f (x0 + tvx , y0 + tvy ). Wtedy
∂f
(x0 , y0 )
∂~v
= F+0 (0).
Gradient funkcji
Definicja 11 Niech istnieją pochodne cząstkowe
f w punkcie (x0 , y0 ) nazywamy wektor
grad f (x0 , y0 ) = (
∂f
(x0 , y0 ), ∂f
(x0 , y0 ).
∂x
∂y
∂f
∂f
(x0 , y0 ),
(x0 , y0 )).
∂x
∂y
Gradientem funkcji
Twierdzenie 2 Niech pochodne
punkcie (x0 , y0 ) ∈ D. Wtedy
∂f ∂f
,
∂x ∂y
istnieją na zbiorze otwartym D i będą ciągłe w
∂f
(x0 , y0 ) = grad f (x0 , y0 ) ◦ ~v .
∂~v
Interpretacja geometryczna
Gradient funkcji w punkcie wskazuje kierunek najszybszego wzrostu funkcji w tym punkcie.
Ekstrema lokalne
Niech f będzie określona na zbiorze otwartym D zawierającym punkt (x0 , y0 ).
Definicja 12 f ma w punkcie (x0 , y0 ) minimum lokalne, jeżeli
_
^
δ>0 (x,y)∈D
[(x, y) ∈ O((x0 , y0 ), δ) ⇒ f (x, y) ­ f (x0 , y0 )].
Twierdzenie 3 (Warunek konieczny istnienia ekstremum)
Niech f będzie określone na otoczeniu punktu (x0 , y0 ). Jeśli f ma ekstremum lokalne w
(x0 , y0 ) i istnieją pochodne cząstkowe ∂f
(x0 , y0 ), ∂f
(x0 , y0 ) to
∂x
∂y
∂f
∂f
(x0 , y0 ) =
(x0 , y0 ) = 0.
∂x
∂y
Twierdzenie 4 (Warunek wystarczający istnienia ekstremum)
Jeżeli f ma ciągłe pochodne cząstkowe rzędu drugiego na otoczeniu punktu (x0 , y0 ) i
∂f
(x0 , y0 ) = ∂f
(x0 , y0 ) = 0 oraz
∂x
∂y

det 
∂2f
(x0 , y0 )
∂x2
2
∂ f
(x0 , y0 )
∂x∂y
∂2f
(x0 , y0 )
∂x∂y
2
∂ f
(x0 , y0 )
∂y 2


>0
to f ma ekstremum lokalne w (x0 , y0 ) i jest to :
2
minimum lokalne właściwe , gdy ∂∂xf2 (x0 , y0 ) > 0 albo
2
maksimum lokalne właściwe, gdy ∂∂xf2 (x0 , y0 ) < 0.
Uwaga 4 Jeśli det[ ] < 0, to f nie ma w (x0 , y0 ) ekstremum lokalnego.
Ekstrema warunkowe
Definicja 13 Funkcja f ma w punkcie (x0 , y0 ) minimum lokalne właściwe z warunkiem
g(x, y) = 0 gdy g(x0 , y0 ) = 0 i
_
^
δ>0 (x,y)∈D
[(x, y) ∈ S((x0 , y0 ), δ) ∧ g(x, y) = 0] ⇒ [f (x, y) > f (x0 , y0 )]
Zbiory domknięte
Niech A będzie zbiorem na płaszczyźnie lub w przestrzeni:
Definicja 14 Punkt P jest punktem brzegowym zbioru A jeżeli
^
r>0
A0 -dopełnienie zbioru A.
O(P, r) ∩ A 6= ∅ oraz O(P, r) ∩ A0 6= ∅.
Definicja 15 Brzegiem zbioru nazywamy zbiór wszystkich jego punktów brzegowych.
Definicja 16 Zbiór jest domknięty jeżeli zawiera swój brzeg.
Definicja 17 Zbiór D jest ograniczony jeżeli jest zawarty w otoczeniu pewnego punktu
__
D ⊂ O(P0 , r).
P0 r>0
Twierdzenie 5 (Weierstrassa o osiąganiu kresów)
Jeżeli zbiór D jest domknięty i ograniczony i funkcja f jest ciągła na D, to
_
f (x1 , y1 ) = sup {f (x, y) : (x, y) ∈ D}
(x1 ,y1 )∈D
_
(x2 ,y2 )∈D
f (x2 , y2 ) = inf {f (x, y) : (x, y) ∈ D}
Znajdowanie wartości największej i najmniejszej funkcji ciągłej na
zbiorze domkniętym
1. Na zbiorze otwartym szukamy punktów, w których funkcja może mieć ekstrema lokalne.
2. Na brzegu zbioru szukamy punktów, w których funkcja może mieć ekstrema lokalne
(ekstrema warunkowe).
Wśród wartości funkcji w tych punktach znajduje się wartość największa i najmniejsza.
Całki podwójne
Całka podwójna po prostokącie
Niech P = {(x, y) : a ¬ x ¬ b, c ¬ y ¬ d} = [a, b] × [c, d]
i P = {P1 , P2 , ..., Pn } będzie podziałem prostokąta P na prostokąty Pk , 1 ¬ k ¬ n.
Oznaczmy
∆xk , ∆yk
-wymiary prostokąta Pk , 1 ¬ k ¬ n,
dk =
q
(∆xk )2 + (∆yk )2
-długość przekątnej prostokąta Pk , 1 ¬ k ¬ n,
δ(P) = max {dk : 1 ¬ k ¬ n}
-średnica podziału P,
(x∗k , yk∗ ) ∈ Pk
-punkt pośredni k-tego prostokąta podziału P, 1 ¬ k ¬ n
Σ = {(x∗k , yk∗ ) : 1 ¬ k ¬ n}
-zbiór punktów pośrednich podziału P.
Niech funkcja f będzie ograniczona na prostokącie P.
Definicja 18 Sumę
σ(f, P) =
n
X
f (x∗k , yk∗ )∆xk ∆yk
k=1
nazywamy sumą całkową.
Ciąg podziałów (Pn ) nazywamy ciągiem normalnym podziałów prostokąta P jeżeli
lim δ(Pn ) = 0.
n→∞
Definicja 19 Całkę podwójną z funkcji f po prostokącie P określamy wzorem
RR
P
f (x, y)dxdy = lim σ(f, Pn )
n→∞
gdzie (Pn ) jest normalnym ciągiem podziałów, o ile granica jest właściwa i taka sama dla
dowolnego normalnego ciągu podziałów (Pn ) oraz nie zależy od sposobów wyboru punktów
pośrednich Σn
Twierdzenie 6 (Warunek wystarczający całkowania funkcji)
Funkcja ograniczona w prostokącie P jest całkowalna, jeżeli wszystkie jej punkty nieciągłości leżą na skończonej ilości krzywych postaci y = y(x) lub x = x(y).
Twierdzenie 7 Jeżeli f i g są całkowalne na prostokącie P oraz c ∈ R, to
RR
P
(f (x, y) + g(x, y))dxdy =
RR
P
RR
P
RR
P
f (x, y)dxdy +
cf (x, y)dxdy = c
f (x, y)dxdy =
RR
P1
RR
P
RR
P
g(x, y)dxdy,
f (x, y)dxdy,
f (x, y)dxdy +
RR
P2
f (x, y)dxdy
gdzie {P1 , P2 } jest podziałem prostokąta P na prostokąty P1 , P2 .
Twierdzenie 8 Jeżeli istnieje
x, to
RR
P
RR
P
f (x, y)dxdy =
f (x, y)dxdy oraz istnieje całka
Rd
f (x, y)dy dla każdego
c
Zb
dx
Zd
f (x, y)dy =
dy
Zb
f (x, y)dx.
a
c
c
a
Zd
Wniosek 1 Niech funkcja f będzie ciągła na prostokącie P = [a, b] × [c, d]. Wtedy
RR
P
f (x, y)dxdy =
Zb
a
dx
Zd
c
f (x, y)dy =
Zd
c
dy
Zb
a
f (x, y)dx.
Interpretacja geometryczna
Niech V = {(x, y, z) : (x, y) ∈ P, 0 ¬ z ¬ f (x, y)} . Wtedy
|V | =
RR
P
f (x, y)dxdy.
Obszary
Definicja 20 Zbiór D ⊂ R2 (R3 ) nazywamy obszarem, jeżeli jest otwarty i każde dwa
punkty zbioru można połączyć łamaną całkowicie w nim zawartą.
Obszar łącznie ze swoim brzegiem nazywamy obszarem domkniętym.
Całka podwójna po obszarze
Niech f będzie funkcją ograniczoną na obszarze ograniczonym D ⊂ R2 .
Niech P będzie dowolnym prostokątem takim, że D ⊂ P. Określamy funkcję
(
∗
f (x, y) =
f (x, y) dla
(x, y) ∈ D
0
dla (x, y) ∈ R2 − D.
Definicja 21 Całkę podwójną z funkcji f po obszarze D określamy wzorem
RR
D
f (x, y)dxdy =
RR
P
f ∗ (x, y)dxdy.
Definicja 22 a) Obszarem normalnym względem osi Ox nazywamy zbiór
{(x, y) : a ¬ x ¬ b, g(x) ¬ y ¬ h(x)}
gdzie funkcje g i h są ciągłe na [a, b] oraz g(x) < h(x) dla każdego x ∈ (a, b).
b) Obszarem normalnym względem osi Oy nazywamy zbiór
{(x, y) : c ¬ y ¬ d, p(y) ¬ x ¬ q(y)}
gdzie funkcje p i q są ciągłe na [c, d] oraz p(y) < q(y) dla każdego y ∈ (c, d).
Twierdzenie 9 Jeżeli funkcja f jest ciągła na obszarze normalnym
a) D = {(x, y) : a ¬ x ¬ b, g(x) ¬ y ¬ h(x)}, to
RR
D
f (x, y)dxdy =
Zb h(x)
Z
f (x, y)dy)dx,
(
a g(x)
b)D = {(x, y) : c ¬ y ¬ d, p(y) ¬ x ¬ q(y)} , to
RR
D
f (x, y)dxdy =
Zd q(y)
Z
(
c p(y)
f (x, y)dx)dy.
Całka podwójna po obszarze regularnym
Definicja 23 Obszar D, który jest sumą skończonej liczby obszarów normalnych ( względem osi Ox lub Oy ) D1 , ..., Dn o parami rozłącznych wnętrzach nazywamy obszarem
regularnym na płaszczyźnie.
Twierdzenie 10 Jeżeli funkcja f jest całkowalna na obszarze regularnym D, to
RR
D
f (x, y)dxdy =
RR
f (x, y)dxdy + ... +
D1
RR
Dn
f (x, y)dxdy.
Zamiana zmiennych w całkach podwójnych
Współrzędne biegunowe
P = (x, y) ≈ (ϕ, ρ),
gdzie ϕ-miara kąta między dodatnią częścią osi Ox a promieniem wodzącym punktu P
0 ¬ ϕ < 2π (albo −π < ϕ ¬ π),
ρ-odległość punktu P od początku układu współrzędnych.
(
B :=
x = ρcosϕ
y = ρsinϕ.
B- przekształcenie, które parze (ϕ, ρ) przyporządkowuje parę (x, y).
Twierdzenie 11 Niech obszar U we współrzędnych biegunowych będzie obszarem normalnym i ma postać
U = {(ϕ, ρ) : α ¬ ϕ ¬ β, g(ϕ) ¬ ρ ¬ h(ϕ)} ,
gdzie funkcje nieujemne g i h są ciągłe na przedziale [α, β] ⊂ [0, 2π]. Niech f będzie ciągła
na obszarze D = B(U ). Wtedy
RR
D
f (x, y)dxdy =
Zβ h(ϕ)
Z
[
α g(ϕ)
RR
U
f (ρcosϕ, ρsinϕ)ρdρdϕ =
f (ρcosϕ, ρsinϕ)ρdρ]dϕ.
Całki potrójne
Całka potrójna po prostopadłościanie
Niech P = {(x, y, z) : a ¬ x ¬ b, c ¬ y ¬ d, p ¬ z ¬ q} = [a, b] × [c, d] × [p, q]
i P = {P1 , P2 , ..., Pn } będzie podziałem prostopadłościanu P na prostopadłościany Pk , 1 ¬
k ¬ n.
Oznaczmy
∆xk , ∆yk , ∆zk
-wymiary prostopadłościanu Pk , 1 ¬ k ¬ n,
dk =
q
(∆xk )2 + (∆yk )2 + (∆zk )2
-długość przekątnej prostopadłościanu Pk , 1 ¬ k ¬ n,
δ(P) = max {dk : 1 ¬ k ¬ n}
-średnica podziału P,
(x∗k , yk∗ , zk∗ ) ∈ Pk
-punkt pośredni k-tego prostopadłościanu podziału P, 1 ¬ k ¬ n
Σ = {(x∗k , yk∗ , zk∗ ) : 1 ¬ k ¬ n}
-zbiór punktów pośrednich podziału P.
Niech funkcja f będzie ograniczona na prostopadłościanie P.
Definicja 24 Sumę
σ(f, P) =
n
X
f (x∗k , yk∗ , zk∗ )∆xk ∆yk ∆zk
k=1
nazywamy sumą całkową.
Ciąg podziałów (Pn ) nazywamy ciągiem normalnym podziałów prostopadłościanu P jeżeli
lim δ(Pn ) = 0.
n→∞
Definicja 25 Całkę potrójną z funkcji f po prostopadłościanie P określamy wzorem
RRR
P
f (x, y, z)dxdydz = lim σ(f, Pn )
n→∞
gdzie (Pn ) jest normalnym ciągiem podziałów, o ile granica jest właściwa i taka sama dla
dowolnego normalnego ciągu podziałów (Pn ) oraz nie zależy od sposobów wyboru punktów
pośrednich Σn
Interpretacja fizyczna całki potrójnej
Niech f oznacza gęstość objętościową masy. Wtedy prostopadłościan P ma masę
M=
RRR
P
f (x, y, z)dxdydz.
Twierdzenie 12 Jeżeli f i g są całkowalne na prostopadłościanie P oraz α ∈ R, β ∈ R,
to
RRR
P
(αf (x, y, z) + βg(x, y, z))dxdydz = α
RRR
P
f (x, y, z)dxdydz =
RRR
P1
RRR
P
f (x, y, z)dxdydz + β
f (x, y, z)dxdydz +
RRR
P2
RRR
P
g(x, y, z)dxdydz,
f (x, y, z)dxdydz
gdzie {P1 , P2 } jest podziałem prostopadłościanu P na prostopadłościany P1 , P2 .
Twierdzenie 13 (O zamianie całki potrójnej na iterowaną)
Niech funkcja f będzie ciągła na prostopadłościanie P = [a, b] × [c, d] × [p, q]. Wtedy
RRR
P
f (x, y, z)dxdydz =
Zb
a
dx
Zd
c
dy
Zq
p
f (x, y, z)dz
Całka potrójna po obszarze
Niech f będzie funkcją ograniczoną na obszarze ograniczonym V ⊂ R3 .
Niech P będzie dowolnym prostopadłościanem zawierającym obszar V. Określamy funkcję
(
∗
f (x, y, z) =
f (x, y, z) dla
(x, y, z) ∈ V
0
dla (x, y, z) ∈ R3 − V.
Definicja 26 Całkę potrójną z funkcji f po obszarze V określamy wzorem
RRR
V
f (x, y, z)dxdydz =
RR
P
f ∗ (x, y, z)dxdydz.
Definicja 27 a) Obszarem normalnym względem płaszczyzny xOy nazywamy zbiór
{(x, y, z) : (x, y) ∈ U, D(x, y) ¬ z ¬ G(x, y)}
gdzie U jest obszarem regularnym na xOy, funkcje D i G są ciągłe na U , przy czym
D(x, y) < G(x, y) dla (x, y) należących do wnętrza obszaru U.
Analogicznie:
b) względem xOz
{(x, y, z) : (x, z) ∈ U, D(x, z) ¬ y ¬ G(x, z)}
c) względem yOz
{(x, y, z) : (y, z) ∈ U, D(y, z) ¬ x ¬ G(y, z)} .
Twierdzenie 14 Jeżeli funkcja f jest ciągła na obszarze
V = {(x, y, z) : (x, y) ∈ U, D(x, y) ¬ z ¬ G(x, y)}
normalnym względem płaszczyzny xOy, gdzie funkcje D i G są ciągłe na obszarze regularnym U , to
RRR
V
f (x, y, z)dxdydz =
RR
(
U
G(x,y)
Z
f (x, y, z))dxdy.
D(x,y)
Jeżeli
U = {(x, y) : a ¬ x ¬ b, d(x) ¬ y ¬ g(x)} ,
gdzie d i g są ciągłe na [a, b], to
RRR
V
f (x, y, z)dxdydz =
Zb
a
dx
g(x)
Z
d(x)
dy
G(x,y)
Z
D(x,y)
f (x, y, z)dz.
Całka potrójna po obszarze regularnym
Definicja 28 Obszar V , który jest sumą skończonej liczby obszarów normalnych ( względem płaszczyzn układu ) V1 , ..., Vn o parami rozłącznych wnętrzach nazywamy obszarem
regularnym na płaszczyźnie.
Twierdzenie 15 Jeżeli funkcja f jest całkowalna na obszarze regularnym V , to
RRR
V
f (x, y, z)dxdydz =
RRR
V1
f (x, y, z)dxdydz + ... +
RRR
Vn
f (x, y, z)dxdydz.
Zamiana zmiennych w całkach potrójnych
Współrzędne walcowe
P = (x, y, z) ≈ (ϕ, ρ, h),
gdzie (ϕ, ρ)- współrzędne biegunowe (x, y),
0 ¬ ϕ < 2π, (−π < ϕ ¬ π), 0 ¬ ρ < ∞, −∞ < h < ∞



x = ρcosϕ
W :=  y = ρsinϕ

z=
h.
W - przekształcenie, które trójce (ϕ, ρ, h) przyporządkowuje trójkę (x, y, z).
Twierdzenie 16 Niech obszar U we współrzędnych walcowych będzie obszarem normalnym i ma postać
U = {(ϕ, ρ, h) : α ¬ ϕ ¬ β, d(ϕ) ¬ ρ ¬ g(ϕ), D(ϕ, ρ) ¬ h ¬ G(ϕ, ρ)} ,
gdzie funkcje nieujemne d i g są ciągłe na przedziale [α, β], a D i G są ciągłe na obszarze
{(ϕ, ρ) : α ¬ ϕ ¬ β, d(ϕ) ¬ ρ ¬ g(ϕ)} .
Jeżeli f jest ciągła na obszarze V = W (U ), to
RRR
V
Zβ
α
dϕ
g(ϕ)
Z
d(ϕ)
dρ
f (x, y, z)dxdydz =
G(ϕ,ρ)
Z
D(ϕ,ρ)
f (ρcosϕ, ρsinϕ, h)ρdh.