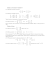Macierze stochastyczne

MACIERZE STOCHASTYCZNE
pij - prawdopodobieństwo przejścia od stanu i do stanu j w jednym (dowolnym) kroku,
P = [pij]- macierz prawdopodobieństw przejść (w jednym kroku),
Własności macierzy prawdopodobieństw przejść:
a)
pij ≥ 0
b) suma każdego wiersza jest równa 1.
Zauważmy też, że w macierzy tej nie może istnieć kolumna złożona z samych zer.
Każdą macierz spełniającą warunki a), b) nazywamy macierzą stochastyczną.
Uwaga.
Macierz stochastyczna i rozkład zmiennej losowej X0 określają pewien łańcuch Markowa.
Własności macierzy stochastycznych są zatem ściśle związane z własnościami łańcuchów
Markowa.
Własności macierzy stochastycznych.
Własność
Średnia arytmetyczna i iloczyn dwóch macierzy stochastycznych tego samego stopnia są
także macierzami stochastycznymi.
Przykład.
0,5 0 0,5
P1 = 0,5 0,5 0 
 0 0,5 0,5
1 / 3 1 / 3 1 / 3
P2 =  0
1
0 
 0,5 0 0,5 
Są macierzami stochastycznymi.
Ich średnia
5 / 12 1 / 6 5 / 12
 0,25 0,75
0 

 0,25 0,25 0,5 
jest macierzą stochastyczną
Ich iloczyn
5 / 12 1 / 6 5 / 12
 1/ 6 2 / 3 1/ 6 


 0,25 0,5 0,25 
jest macierzą stochastyczną
A - dowolna macierz kwadratowa stopnia r.
Wielomianem charakterystycznym tej macierzy nazywamy wielomian
W (λ ) = det(λI − A)
Równanie W (λ ) = 0 nazywamy równaniem charakterystycznym. Pierwiastki tego
równania to wartości własne lub pierwiastki charakterystyczne tej macierzy.
Niech λ1, ...., λk - wartości własne macierzy A o krotnościach α1, ...., αk (k ≤ r).
Wektorem własnym operatora f odpowiadającym wartości własnej λ nazywamy niezerowy
wektor v spełniający warunek f(v) = λv.
Własność:
I)
suma wartości własnych (z krotnościami) jest równa śladowi macierzy tzn. sumie
elementów jej przekątnej.
II)
Macierz jest osobliwa wtedy i tylko wtedy gdy zero jest jej wartością własną
Przykład.
1
4
Macierz P =  2

3
3
4
1  ma równanie charakterystyczne

3
1
3 

λ − 4 − 4 
7 5
W (λ ) = det 
= λ2 − λ −
=0

2
1
12
12
 −
λ− 
3
 3
i wartości własne: λ1 =1, λ 2 =
−5
.
12
Własności macierzy stochastycznych:
a) Wartością własną każdej macierzy stochastycznej jest λ = 1 (oznaczamy λ1 =1),
Dowód.
Dodajemy wszystkie kolumny macierzy
(λI − A) do pierwszej kolumny, sumy wierszy są
równe 1 więc po dodaniu wszystkie elementy pierwszej kolumny są równe λ - 1 i można tą
wartość wyłączyć przed wyznacznik.
b) Moduły wszystkich wartości własnych dowolnej macierzy stochastycznej są mniejsze
od 1,
1 n k
P = A,
∑
n →∞ n
k =1
c) (tw. Dooba ) istnieje granica lim
Macierz A ma własność PA = AP = A = A2 (macierz idempotentna),
Klasyfikacja macierzy stochastycznych.
∧
λi
i >1
α1 = 1
α1 > 1
Regularne
rozkładalne
(tzn. nierozkładalne i niecykliczne)
niecykliczne
nierozkładalne
rozkładalne
cykliczne
cykliczne
≠1
∨ λi = 1
i >1
Tw. Frecheta (tw. Dooba dla macierzy nierozkładalnych)
Dla każdej nierozkładalnej macierzy stochastycznej P istnieje granica
1 n k
P = E,
∑
n →∞ n
k =1
lim
 e1
e
E= 1
L

 e1
e2
e2
L
e2
L
L
L
L
er 
er 
L

er 
(macierz ergodyczna)
Macierz E ma własność PE = EP = E = E2 i spełnia warunki a), b) definicji macierzy
stochastycznej. Elementy macierzy E możemy wyznaczyć z warunków:
(P - I)eT = 0,
r
∑e
i =1
i
= 1,
gdzie e = (e1, ...., er )
Dla macierzy regularnych tw. Dooba ma postać:
Twierdzenie.
Jeśli macierz stochastyczna P jest regularna to istnieje granica
lim P n = E ,
n →∞
gdzie E - macierz ergodyczna.
Stochastyczne macierze regularne charakteryzuje też tzw. twierdzenie ergodyczne:
Twierdzenie.
Jeśli macierz stochastyczna P jest regularna to istnieje taka jej potęga w której co najmniej
jedna kolumna ma wszystkie elementy dodatnie.
Przykład.
Macierz
λ1 =1, λ 2 =
0
0,5 
0,5
P =  0 0,25 0,75
0,5 0,5
0 
ma wartości własne
− 1 + 17
− 1 − 17
, λ3 =
więc jest macierzą regularną.
8
8
Przykład.
Macierz
0 0,5 0,5
0
0

0
0
,
5
0
,
5
 ma wartości własne
P=
0,5 0,5 0
0


0
0,5 0,5 0
λ1 =1, λ 2 = −1 , λ3 = 0 o krotności 2, więc jest macierzą cykliczną nierozkładalną.
Macierz ta ma własność
 P gdy n nieparzyste
Pn =  2
.
 P gdy n parzyste
Przykład.
Macierz
1
2
1

2
P = 0
0


0

1
0
2
1
0
2
0 1
0
0

0

0

0
2
3
3

4
0
0
0
1
0
3
1
0
4
λ1 =1 o krotności 3, λ 2 = 0 , λ3 =
ma wartości własne
1
, więc jest macierzą niecykliczną rozkładalną.
12
Macierz stochastyczna rozkładalna (po ewentualnym przestawieniu wierszy i kolumn) ma
bloki diagonalne, które są macierzami stochastycznymi. Wartościami własnymi macierzy P są
wartości własne poszczególnych bloków. W tym przykładzie są trzy bloki diagonalne.
Przykład.
Macierz
0,5 0,5 0 0
0,5 0,5 0 0

P=
0
0 0 1


0 1 0
0
ma wartości własne
λ1 =1 o krotności 2, λ 2 = 0 , λ3 = −1 , więc jest macierzą cykliczną rozkładalną.
Macierz przywiedlna.
Macierz kwadratowa P stopnia n nazywa się przywiedlna, jeśli przez odpowiednie
permutacje wierszy i kolumn można przekształcić P do postaci
B
C

0
D 
gdzie B, D są kwadratowe.
W przeciwnym przypadku macierz P nazywa się nieprzywiedlna.
Macierz dodatnia jest nieprzywiedlna,
Jeśli macierz ma zerowy wiersz lub kolumnę zerową to jest przywiedlna.
Macierz diagonalna lub trójkątna jest przywiedlna.
Postać normalna macierzy stochastycznej.
Postać normalna macierzy stochastycznej P stopnia n to macierz
T1 0
0 T
2

L L
0 0

R

0
L 0 0 
L
L 
L Tg 0 

S
L
0
Otrzymana z P przez odpowiednie permutacje wierszy i kolumn, gdzie
Ti to macierze stochastyczne i nieprzywiedlne, 1 ≤ g ≤ n, g = krotność wartości własnej 1.
S kwadratowa, niestochastyczna i nieprzywiedlna (jeśli istnieje).
Przykład.
Macierz
0 0,5
0,5 0
 0 0,5 0,5 0 

P=
 0 0,5 0,5 0 


0 0,5
0,5 0
ma wartości własne λ1 =1 o krotności 2, λ 2 = 0 o krotności 2.
Jej postać normalna
0
0,5 0,5 0
0,5 0,5 0
0 

0
0 0,5 0,5


0 0,5 0,5
0
0,5 0,5

0,5 0,5
Ma dwie macierze stochastyczne T1 = T2 = 
Brak macierzy S i R.
Przykład.
Macierz
0
0
0
1
0

1
0
0

P=
0,5 0,5 0
0


0 0,5 0,5
0
ma wartości własne λ1 =1 o krotności 2, λ 2 = 0 , λ 2 = 0,5 . Jest to macierz rozkładalna
niecykliczna.
Jej postać normalna jest taka jak P
0
0
0
1
0
1
0
0 

0,5 0,5 0
0


0 0,5 0,5
0
Ma dwie macierze stochastyczne T1 = T2 = [1],
0
0,5 0,5
0
R=
, S=


0
0
0,5 0,5
ZADANIA
Zadanie 1.
Wyznacz wartości własne i ich krotności dla macierzy
0
0,5 
0,5

P =  0 0,25 0,75
0,5 0,5
0 
Do jakiej klasy należy ta macierz?
Zadanie 2.
Wyznacz wartości własne i ich krotności dla macierzy
 0,1 0,9
0,2 0,8
P=
0
0

0
0
0 0
0 0
0 1

1 0
Do jakiej klasy należy ta macierz?
Zadanie 3.
Wyznacz wartości własne i ich krotności dla macierzy
0 1 0 
P = 1 0 0
0 0 1
Do jakiej klasy należy ta macierz?
k
P ?
Czy istnieje lim
n →∞
1 n k
P ?
Czy istnieje lim
∑
n →∞ n
k =1
Zadanie 4.
Wyznacz wartości własne i ich krotności dla macierzy
1 / 3 1 / 3 1 / 3
P =  0
0
1 
 0
1
0 
Do jakiej klasy należy ta macierz?
Czy istnieje lim P k ?
n →∞
1 n k
Czy istnieje lim ∑ P ?
n →∞ n
k =1
Zadanie 5.
Wyznacz wartości własne i ich krotności dla macierzy
0,2 0,1 0,7
P =  0
0
1 
 0
1
0 
Do jakiej klasy należy ta macierz?
Przedstaw macierz P w postaci normalnej.
L.Kowalski, 22.10.09