Regionalne Koło Matematyczne

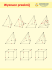
Regionalne Koło Matematyczne
Uniwersytet Mikołaja Kopernika w Toruniu
Wydział Matematyki i Informatyki
http://www.mat.umk.pl/rkm/
Lista rozwiązań zadań nr 19 (20.03.2010)
Zastosowania izometrii
Pragniemy pokazać zastosowania izometrii na przykładzie zadań konstrukcyjnych
i rozwiązywania zadań ekstremalnych w geometrii. Zilustrujemy to na przykładzie
rozważań w kilku zadaniach.
1. Dane są dwa okręgi przecinające się w punktach A i B. Przez punkt A poprowadzić prostą, która nie przechodzi przez punkt B i która wycina w okręgach
cięciwy tej samej długości.
Rozwiązanie. Analiza.
Skoro cięciwa XA ma być równa AY , to punkt A jest środkiem odcinka XY
lub inaczej: Y jest obrazem punktu X w symetrii środkowej SA , tzn. Y jest
punktem wspólnym okręgu o2 i obrazu okręgu o1 w symetrii SA .
X
o1
A
Y
B
o2
Konstrukcja.
1) Konstruujemy obraz okręgu o1 w symetrii SA .
2) Znajdujemy punkty wspólne o2 i SA (o1 ). Są nimi A i Y .
1
3) Przez punkty A i Y prowadzimy prostą m.
Niech m przecina okrąg o1 w punkcie X. Zauważmy, że Y = SA (X) (!). Zatem
|AX| = |AY |.
2. Skonstruować trójkąt mając dane dwa środki boków i prostą zawierającą dwusieczną poprowadzoną do jednego z tych boków.
Rozwiązanie. Analiza.
Dane są punkty M, N – środki boków AC i BC oraz prosta n zawierająca
dwusieczną kąta BAC. Wiadomo, że prosta n jest osią symetrii kąta BAC.
Zatem obraz punktu M w symetrii osiowej Sn leży na ramieniu AB. Ponadto
prosta AB jest równoległa do prostej MN.
C
n
M
N
A
B
Konstrukcja.
1) Znajdujemy punkt M ′ będący obrazem punktu M w symetrii osiowej Sn .
2) Prowadzimy przez punkt M ′ prostą równoległą do prostej MN.
3) Punkt przecięcia prostej poprowadzonej w punkcie 2) z prostą n jest wierzchołkiem A.
4) Mając wierzchołek A łatwo konstruujemy wierzchołki C i B.
3. Opisać konstrukcję trójkąta równobocznego, którego wierzchołki leżą na trzech
danych prostych równoległych.
Rozwiązanie tego zadania znajduje się na liście rozwiązań zadań grupy zaawansowanej.
4. Punkty A i B leżą w jednej z półpłaszczyzn wyznaczonych przez prostą p. Na
prostej p znaleźć taki punkt X, aby suma |AX| + |BX| była najmniejsza.
Rozwiązanie. Niech A′ = Sp (A) i niech X będzie punktem przecięcia prostej p
i prostej AB. Pokażemy, że dla dowolnego punktu Y ∈ p zachodzi nierówność
|AX| + |XB| 6 |AY | + |Y B|.
2
B
A
X
Y
A′
Zauważmy, że
|A′ B| = |A′ X| + |XB| = |AX + |XB|.
Z drugiej strony
|A′ B| 6 |A′ Y | + |Y B| = |AY | + |Y B|.
5. Dany jest kąt ostry AOB i punkt P leżący wewnątrz tego kąta. Poprowadzić
prostą przez ten punkt tak, aby odcięła od kąta trójkąt o najmniejszym polu.
Rozwiązanie. Poprowadźmy przez punkt P dwie proste, które przecinają ramiona kąta w punktach M, N oraz X, Y i niech |MP | =
6 |NP |, tzn. punkt P
nie jest środkiem odcinka MN.
B
M
X
P
X′
O
N
Y
A
Zauważmy, że N = SP (M), SP – symetria środkowa. Niech X ′ = SP (X), gdy
|P X| < |P Y |, w przeciwnym wypadku weźmiemy Y ′ = SP (Y ). Oczywistym
jest, że P△XM P = P△X ′ N P – pola trójkątów XMP i X ′ NP są równe. Wówczas
P△OXY = PON P X +P△N X ′ P +P△N X ′ Y > PON P X +P△N X ′ P = PON P X +P△XP M = P△ON M .
Zatem minimalne pole otrzymamy wtedy, gdy prosta przechodząca przez punkt
P przecina ramiona tak, by punkt P był środkiem odcinka, którego końcami
są punkty przecięcia prostej z ramionami kąta.
6. Zadanie Schwarza. Dany jest trójkąt ostrokątny ABC. Wyznaczyć punkty P ,
Q, R leżące odpowiednio na bokach AB, BC, CA tego trójkąta tak, aby obwód
trójkąta P QR był najmniejszy.
Rozwiązanie tego zadania znajduje się na liście rozwiązań zadań grupy zaawansowanej.
3