Metoda Eulera, Newtona, twierdzenie Pascala i grupa na krzywej

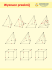
Metoda Eulera, Newtona, twierdzenie Pascala
i grupa na krzywej stożkowej
Przetnijmy parabolę poziomą prostą l. Wybierzmy dwa punkty A, B leżące
na paraboli. Załóżmy na początek, że A 6= B oraz, że prosta AB przecina
prostą l. Poprowadźmy przez punkt przecięcia prostej l z prostą AB prostą
pionową. Prosta ta przetnie parabolę w nowym punkcie, który oznaczymy
symbolem A + B.
A
B
l
A+B
Umawiamy się, że w przypadku, kiedy A = B zamiast prostej przechodzącej przez punkty A, B rysujemy styczną do paraboli w punkcie A. Poza tym
umawiamy się, że w przypadku, kiedy proste się nie przecinają, A + B = ∞.
Okazuje się, że tak określone działanie definiuje pewną grupę przemienną.
Elementem neutralnym jest punkt ∞. Dowód łączności pozostawimy na
koniec.
Metoda Eulera pozwala znaleźć punkt przecięcia osi poziomej z krzywą.
Wybieramy dwa punkty A1 , A2 , a dalsze punkty znajdujemy stosując wzór
rekurencyjny An+1 = An−1 + An .
Metoda Newtona działa szybciej. Wybieramy pewien punkt A0 i znajdujemy kolejne punkty stosując wzór An+1 = 2An .
A teraz zobaczmy, jak można określić w podobny sposób dodawanie punktów na elipsie.
W tym celu wybierzmy pewną prostą l i jakiś punkt O na elipsie. Zakładamy, że punkt O nie leży na prostej l.
Załóżmy na początek, że A 6= B, A 6= O, B 6= O oraz, że prosta AB
przecina prostą l. Prowadzimy prostą przez punkty O i punkt przecięcia
prostej AB z prostą l. Prosta ta przetnie elipsę w drugim punkcie, który
oznaczymy symbolem A + B.
1
W przypadku, kiedy A = B zamiast prostej AB rozpatrujemy styczną
do elipsy w punkcie A. Jeśli prosta AB jest równoległa do prostej l, to
umawiamy się, że A + B = O. Poza tym umawiamy się, że A + O = A.
A
O
l
B
A+B
Dowód łączności wykorzystuje twierdzenie Pascala.
Popatrzmy na pierwszy rysunek.
Twierdzenie Pascala mówi, że jeśli odpowiednie linie przecinają się po trzy
w ośmiu dowolnie wybranych punktach, to przetną się również pozostałym
dziewiątym punkcie.
A
O
l
C
S
R
B
Q=B+C
P=A+B
Dowód łączności. Niech P = A + B i Q = B + C. Z twierdzenia Pascala
wynika, że proste P C i AQ przecinają prostą l w tym samym punkcie S.
Dlatego R = A + (B + C) = (A + B) + C.
Jerzy Cisło
2