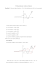Regionalne Koło Matematyczne

Regionalne Koło Matematyczne
Uniwersytet Mikołaja Kopernika w Toruniu
Wydział Matematyki i Informatyki
http://www.mat.umk.pl/rkm/
Lista rozwiązań zadań nr 18 (13.03.2010)
O izometriach (c.d.)
Wektorem uporządkowanej pary prostych równoległych (a, b) nazywamy wektor ~u
równy wektorowi, którego początek znajduje się na prostej a, a koniec na prostej b
−→
oraz wektor ten jest prostopadły do prostych a, b. Wektor ten oznaczamy (a, b).
Translacją (przesunięciem) o wektor ~u nazywamy przekształcenie, które punktowi
−−→
X ∈ P przyporządkowuje taki punkt X ′ , że XX ′ = ~u. Translację oznaczamy symbolem Tu~ .
1. Udowodnić, że Sb ◦ Sa , gdy a k b, jest przesunięciem.
Rozwiązanie. Niech X będzie dowolnym punktem płaszczyzny. Oznaczmy
X1 = Sa (X) i
X ′ = Sb (X1 ) = Sb (Sa (X)) = Sb ◦ Sa (X).
d
x
X
Y1
d−x
x
X1
y
y
d−x
X′
d+y
Y
Y′
Zauważmy, że prosta XX ′ jest prostopadła do prostych a i b. Ponadto
|XX ′ | = x + x + d − x + d − x = 2d.
1
Odległość między X i X ′ równa jest dwukrotnej odległości między prostymi a
i b. Podobne rozważania mamy dla punktu Y . Czytelnik zechce rozważyć inne
położenia punktu X.
−−→
−→
→ (X).
Podsumowując, widzimy, że XX ′ = 2 · (a, b), tzn. X ′ = T2·(−
a,b)
2. Udowodnić, że każdą translację można przedstawić jako złożenie dwóch symetrii osiowych o osiach równoległych.
Rozwiązanie. Niech dana będzie translacja Tu~ . Jeśli ~u = ~0, to Tu~ = 1P = Sa ◦ Sa ,
gdzie a jest dowolną prostą.
Niech ~u będzie wektorem niezerowym. Wybierzmy dwie proste równoległe a,
−→
b takie, że (a, b) = 12 ~u. Wówczas istotnie Tu~ = Sb ◦ Sa .
−→
−→
Wniosek. Sb ◦ Sa = Sd ◦ Sc wtedy i tylko wtedy, gdy (a, b) = (c, d).
3. Jeśli proste a, b, c przecinają się w punkcie O, to Sc ◦Sb ◦Sa jest symetrią osiową.
Rozwiązanie. Dowód jest identyczny jak dla translacji, korzystamy z faktu, że
Sy ◦ Sx = Sz ◦ St wtedy i tylko wtedy, gdy ∠(x, y) = ∠(t, z).
4. Zbadać, jakim przekształceniem jest złożenie dwóch, trzech symetrii środkowych.
Rozwiązanie. Zauważmy, że symetrię środkową można uważać za obrót o
180◦ . Zatem złożenie dwóch symetrii środkowych jest translacją, a złożenie
trzech symetrii środkowych jest obrotem o kąt 3 · 180◦, a więc jest symetrią
środkową.
Czytelnikom pozostawiamy inne rozwiązanie powyższego zadania.
Uogólnienie. Złożenie parzystej liczby symetrii środkowych jest translacją, a
złożenie nieparzystej liczby symetrii środkowych jest symetrią środkową.
2