rozkład gamma

Wybrane rozkłady zmiennych
losowych
Matematyczne podstawy teorii
ryzyka i ich zastosowanie
R. Łochowski
Rozkłady dyskretne
• Rzeczywista zmienna losowa X ma rozkład
dyskretny jeżeli wartości które przyjmuje
można ponumerować liczbami naturalnymi
(
)
P X ∈ {x 1, x 2 ,...} = 1
• Oznaczmy ∞pi = P (X = x i ), i = 1,2,...,
wówczas ∑ pi = 1, oraz dla dowolnego zbioru
i =1
liczb rzeczywistych A
P (X ∈ A ) =
∑p
x i ∈A
i
Przykłady rozkładów dyskretnych
• Rozkład 0-1:
P (X = 0) = q, P (X = 1) = p, p ∈ (0,1), p + q = 1
• Rozkład dwumianowy Bin(n,p):
n 
  k n −k
P (X = k ) =   p q , k = 0,1,..., n
k 
• Rozkład geometryczny Geom(q)
P (X = k ) = pq k , k = 0,1,..., ∞
• Rozkład Poissona Poi(λ)
P (X = k ) = e
−λ
k
λ
, k = 0,1,..., ∞
k!
Podstawowe charakterystyki
rozkładów dyskretnych
• Wartość oczekiwana – średnia ważona
wartości, które przyjmuje zmienna z wagami
odpowiadającymi prawdopodobieństwom ich
∞
przyjęcia
EX = ∑ pi x i
i =1
• Wariancja i odchylenie standardowe:
∞
2
D X = ∑ pi (x i − EX ) , DX = D X
2
2
i =1
• Obliczyć wartość oczekiwaną i wariancję
rozkładu geometrycznego i rozkładu Poissona
Rozkład geometryczny i rozkład
ujemny dwumianowy
• Jeżeli X = liczba porażek w nieskończonym
schemacie Bernoulliego do uzyskania 1.
sukcesu, to X ma rozkład geometryczny
• Jeżeli Y = liczba porażek w nieskończonym
schemacie Bernoulliego do uzyskania r.
sukcesu, to X ma rozkład ujemny dwumianowy
NegBin(r,q)
k + r − 1

 p rq k , k = 0,1,..., ∞
P (Y = k ) = 

k


• Zadanie: Uzasadnić powyższą równość
Charakterystyki ujemnego rozkładu
dwumianowego
• Jeżeli X1, X 2 ,..., X r są niezależne i mają rozkład
Geom(q), wówczas Y = X1 + X 2 + ...X r
ma rozkład NegBin(r, q), stąd
EY = rEX1 = rqp −1, D2Y = rD2X1 = rqp −2
• Uogólnienie rozkładu ujemnego
dwumianowego – r jest dowolną liczbą
dodatnią oraz
k + r − 1 r (r + 1) ⋅ ... ⋅ (r + k − 1)

=



k
k!


Rozkłady ujemne dwumianowe
r = 10;
p = 0.2 (niebieski), p = 0.5 (zielony)
p = 0.8 (czerwony)
Źródło: Wikipedia
Rozkłady ciągłe
• Niektóre zmienne losowe mogą przyjmować
wszystkie wartości z pewnego przedziału liczb
rzeczywistych a, b  , −∞ ≤ a < b ≤ +∞, których
 
nie da się ponumerować za pomocą liczb
naturalnych
a, b  →  0, +∞), że
• Jeżeli
istnieje
taka
funkcja
g
:
 

b
∫ g (x )dx = 1 oraz dla a ≤ c < d ≤ b
a
(
)
P X ∈ c, d  = ∫ g (x )dx ,
c
to mówimy, że zmienna losowa X jest ciągła i ma
gęstość g
d
Przykłady rozkładów ciągłych i ich
gęstości
• Rozkład jednostajny na przedziale [a,b], U[a,b]
d −c
1


P X ∈ c,d  =
,a ≤ c < d ≤ b, g (x ) =
,a ≤ x ≤ b
b −a
b −a
(
)
• Rozkład wykładniczy Exp(λ)
(
)
P X ∈ c,d  = e−λc − e−λd ,0 ≤ c < d, g (x ) = λ e−λx ,0 ≤ x < ∞
• Rozkład normalny N(μ,σ2)
(
)
P X ∈ c, d  = Φ (d ) − Φ (c ), −∞ ≤ c < d ≤ ∞
2
2
a
−(x −µ) /(2 σ 2 )
−(x −µ) /(2 σ 2 )
1
1
Φ (a ) =
e
dx , g (x ) =
e
∫
2πσ −∞
2πσ
Gęstości rozkładu normalnego
Źródło: Wikipedia
Charakterystyki rozkładów ciągłych
• Wartość oczekiwaną zmiennej o rozkładzie
ciągłym definiujemy za pomocą wzoru
∫
EX =
b
a
x ⋅ g (x )dx
• Wariancję zmiennej o rozkładzie ciągłym
definiujemy za pomocą wzoru
DX =
2
∫ (x − EX )
b
2
a
⋅ g (x )dx
• Zadanie: udowodnić, że
DX =
2
∫
b
a
x ⋅ g (x )dx − (EX )
2
2
Rozkład gamma
• Jeżeli X1, X 2 ,..., X r są niezależne i mają rozkład
Exp(λ), wówczas o zmiennejY = X1 + X 2 + ...X r
mówimy, że ma rozkład gamma z parametrami
λ i r, Γ(r, λ), o gęstości
g (x ) =
λr
(r − 1)!
x r −1 e−λx , 0 ≤ x < +∞
• Uwaga: powyższa funkcja jest gęstością dla
dowolnego r>0, jeżeli zdefiniujemy
(r − 1)! = Γ (r ) := ∫
∞
0
x
r −1
−x
e dx
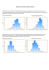
Gęstości rozkładu gamma
k=r, θ=1/λ
Źródło: Wikipedia
Charakterystyki rozkładu gamma
• Zadanie: obliczyć wartość oczekiwaną i
wariancję rozkładu wykładniczego a następnie
wartość oczekiwaną i wariancję rozkładu Γ(r, λ)
• Zadanie: obliczyć wartość oczekiwaną i
wariancję rozkładu Γ(r, λ) korzystając z
ogólnych wzorów na wartość oczekiwaną i
wariancję rozkładu ciągłego
Charakterystyki rozkładu gamma odpowiedzi
• Wartość oczekiwana rozkładu Γ(r, λ)
r
EX =
λ
• Wariancja rozkładu Γ(r, λ)
r
DX = 2
λ
2
• Drugi moment zwykły (wartość oczekiwana
kwadratu)
r (r + 1)
EX 2 =
λ2