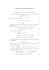Ekonometria Lista 9 Z2ZF01 Lista zadań obejmuje następujące

Ekonometria
Lista 9
Z2ZF01
Lista zadań obejmuje następujące zagadnienia:
• Modele jakościowych cech zależnych
• Liniowy model prawdopodobieństwa
• Liniowy model regresji logistycznej
Modele jakościowych cech zależnych
Rozważania ograniczymy do binarnej cechy zależnej, tzn. będziemy zakładać, że zmienna objaśniana Y może przyjmować dwie wartości: 0 lub 1. Często modele tego typu pojawiają się, gdy
interesują nas przyczyny podejmowania określonych decyzji przez jednostki, np.:
• Dlaczego część ludzi podejmuje studia, podczas gdy inni nie?
(Yi = 1 jeśli i-ta osoba podjęła studia, Yi = 0 w przeciwnym wypadku; X = (X1 , . . . , Xm )
– zbiór m czynników, które mogą mieć wpływ na podjętą decyzję, np. płeć, wykształcenie
rodziców, dochody, itp.)
• Dlaczego niektórzy przedsiębiorcy decydują się na zakup samochodów, podczas gdy inni
wybierają leasing?
Innym popularnym zastosowaniem tego typu modeli jest ocena zdolności kredytowej (credit scoring).
W rozpatrywanym do tej pory liniowym modelu ekonometrycznym modelowano za pomocą liniowego predyktora η = Xα = α0 +α1 X1 +· · ·+αm Xm warunkową wartość oczekiwaną ilościowej
b |X) = ηb = Xα.
b
zmiennej Y : E(Y |X) = η = Xα. W wyniku estymacji otrzymywano: Yb = E(Y
Zauważmy, że binarna zmienna Y posiada rozkład zero-jedynkowy, tzn. przyjmuje wartość 1
z prawdopodobieństwem Pr(Y = 1|X) oraz wartość 0 z prawdopodobieństwem Pr(Y = 0|X) =
1 − Pr(Y = 1|X). Uogólnimy też rozważania do przypadku, w którym warunkowa wartość
oczekiwana modelowana jest za pomocą pewnej monotonicznej funkcji liniowego predyktora, tj.
E(Y |X) = g(η).
1
Pokazać, że w przypadku binarnej zmiennej objaśnianej E(Y |X) = Pr(Y = 1|X).
Liniowy model prawdopodobieństwa
Jest to najprostszy model, w którym zakłada się, że funkcja g jest tożsamościowa:
Pr(Y = 1|X) = η = Xα.
(1)
Parametry liniowego modelu prawdopodobieństwa można oszacować za pomocą KMNK.
Liniowy model regresji logistycznej (logitowy)
W modelu tym zakłada się, że g jest funkcją logistyczną:
Pr(Y = 1|X) =
1
1
=
.
1 + exp(−η)
1 + exp(−Xα)
Parametry modeli logitowych można oszacować Metodą Największej Wiarogodności.
1
(2)
Ekonometria
Lista 9
Z2ZF01
2
W 18-sto osobowej grupie studentów ekonometrii przeprowadzono test zaliczeniowy. Postawiono
hipotezę, że prawdopodobieństwo zdania testu zależy w sposób liniowy od liczby dni jakie i-ty
student poświęcił na naukę tuż przed testem (Xi ). Yi jest zmienną sztuczną, przyjmującą wartość
1 jeśli i-ty student zdał test, a 0 w przeciwnym wypadku. Na podstawie poniższych danych:
i
1
2
3
4
5
6
7
8
9
Yi
0
0
0
0
0
0
0
1
0
Xi
5
5
5
6
6
6
7
7
10
i
10
11
12
13
14
15
16
17
18
Yi
1
0
1
1
0
1
1
1
1
Xi
10
10
11
11
12
12
12
12
12
a)
b)
c)
d)
Zapisać liniowy model prawdopodobieństwa.
Oszacować parametry modelu.
Podać interpretację wartości oszacowanych parametrów.
Wyznaczyć wartości prawdopodobieństwa Pr(Y = 1|X) oraz reszty modelu ei . Jakie
mankamenty liniowego modelu prawdopodobieństwa dostrzegasz?
e) Stworzyć wykres linii regresji.
3
Pokazać, że dla modelu logitowego (2), gdzie Pi = Pr(Yi = 1|Xi ):
a)
b)
c)
d)
Pi = exp(Xi α)/[1 + exp(Xi α)]
exp(Xi α) = Pi /(1 − Pi )
(iloraz szans, ang. odds)
ln[Pi /(1 − Pi )] = Xi α
(logarytm ilorazu szans, ang. log odds)
1 − Pi = 1/[1 + exp(Xi α)]
4
Pokazać, że logarytm naturalny funkcji wiarogodności ` dla n-elementowej próby dla modelu
logitowego (2) wyraża się następującym wzorem:
ln ` =
n
X
i=1
Yi · Xi α −
n
X
ln[1 + exp(Xi α)].
(3)
i=1
Wskazówki:
a) Zmienna losowa Y ma rozkład zero-jedynkowy: Pr(Y = Yi ) = PiYi ·(1−Pi )1−Yi , Yi ∈ {0, 1}.
b) Skorzystać z równości z zadania 3.
2
Ekonometria
Lista 9
Z2ZF01
5
Na podstawie obserwacji zmiennych z zadania 2 oszacować parametry modelu logitowego, maksymalizując logarytm naturalny funkcji wiarogodności ` podany w zadaniu 4. Skorzystać z narzędzia Solver w programie MS Excel. Jako początkowe wartości oszacowań parametrów przyjąć
oszacowania MNK z zadania 2.
Na wykres z zadania 2(e) nanieść wartości prawdopodobieństwa Pi wyznaczone na podstawie
oszacowanego modelu logitowego.
Aby oszacować wpływ zmiany liczby dni, jakie i-ty student poświęcił na naukę tuż przed testem
(Xi ) na prawdopodobieństwo zdania testu, należy wyznaczyć pochodną funkcji g(α1 X + α0 ) po
X. Pokazać, że
∂g(α1 X + α0 )
exp(−(α1 X + α0 ))
=
· α1
∂X
[1 + exp(−(α1 X + α0 ))]2
(4)
a) Wyznaczyć i zinterpretować wartości pochodnej dla X̄, X = 5, X = 12. Dla każdej
wartości X obliczyć prawdopodobieństwo zdania testu Pi .
b) Porównać interpretację oszacowania parametru α1 z zadania 2 z interpretacją wartości
pochodnej w punkcie X = X̄.
6
Historia współpracy pewnego banku z klientami pozwoliła stworzyć próbę uczącą, składającą się
z klientów dobrych, którzy spłacili kredyt bez większych problemów, oraz klientów złych, którzy
mieli trudności w spłacie kredytu. Na podstawie tej próby oszacowano dla celów aplikacyjnego
credit scoringu liniowy model prawdopodobieństwa:
Ybi = −0.475 + 0.234HOM Ei + 0.02IN Ci + 0.002AGEi − 0.011LOANi ,
gdzie: Y to zmienna przyjmująca wartość 1, gdy klient był dobry oraz 0 — gdy klient okazał
się zły, HOM E to zmienna przyjmująca wartość 1, gdy klient był właścicielem domu oraz 0
w przeciwnym razie, IN C oznacza przeciętny roczny dochód klienta z ostatnich 3 lat w tys.
USD, AGE to wiek klienta w latach, a LOAN to kwota kredytu w tys. USD.
a) Stosując standardową regułę mikroprognozy (punkt odcięcia 12 ), zakwalifikować do odpowiedniej grupy ryzyka 30-letniego aplikanta, który nie jest właścicielem domu, jego przeciętny roczny dochód z ostatnich trzech lat wyniósł 35 tys. USD, a wniesiono o kredyt
w wysokości 8 tys. USD.
b) Wiedząc, że diag(XT X) = (60, 37, 128806, 73385, 6212) podać liczbę obserwacji tworzących próbę uczącą .
c) Podać próbkową liczbę kredytowo wiarygodnych klientów, jeśli w próbie otrzymano Ȳ =
0.55.
3