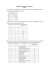1. Sprawdzić czy dany schemat jest tautologią rachunku zdań. 1.1

AlgTM, Kolokwium I, zima 2013/2014, A.Sz.
1. Sprawdzić czy dany schemat jest tautologią rachunku zdań.
1.1. [q ∨(∼ r ⇒ q)∨r∨ ∼ p] ⇒ [(∼ p∧r)∨(p ⇒ q)]
1.2. [(p ⇒ r)∧ ∼ (∼ q ∨p)] ⇒ [q∧ ∼ (r ⇒∼ q)∧(r ⇒ p)]
2. Czy dany schemat jest prawem rachunku kwantyfikatorów? Podać dowód lub kontrprzykład.
2.1. [∃x ∈ X (φ(x) ⇒ ψ(x))] ⇒ [(∃x ∈ X φ(x)) ∨ (∀x ∈ X ψ(x))]
2.2. [∀x ∈ X (φ(x) ⇒ ψ(x))] ⇒ [(∃x ∈ X φ(x)) ⇒ (∃x ∈ X ψ(x))]
3. Wyznaczyć zbiór elementów x ∈ R spełniających formę zdaniową ϕ(x).
3.1. ϕ(x) : ∃y x · y = 1
3.2. ϕ(x) : ∀y x · y 6= 1
3.3. ϕ(x) : ∃y x < sin y
3.3. ϕ(x) : ∀y x2 + y 2 > 5
4. Sformułować implikację odwrotną, przeciwną i przeciwstawną do implikacji y ¬ |x| ⇒ |x| + |y| < 2.
Dla każdej z tych implikacji zaznaczyć na płaszczyźnie zbiór punktów, które ją spełniają.
5. Wykazać metodą indukcji matematycznej.
2
2
5.1. ∀n ∈ N+ 13 + 23 + ... + n3 = n (n+1)
4
5.2. ∀n ∈ N0 25|2n+2 · 3n + 5n − 4
5.3. ∀n ∈ N+ 1 · 1! + 2 · 2! + ... + n · n! = (n + 1)! − 1
6. Udowodnić równość lub podać kontrprzykład.
6.1. [(C ∪ A) ÷ B] ∪ (A ∩ B) = A ∪ (B − C)
6.2. (A − B) − C = A − (B ∪ C)
7. Sprawdzić, czy zbiory A = ∅, B = {∅, {∅}} i C = {∅, 2} spełniają równość
(A ∪ C) ÷ B = (A − C) ∪ (B ∩ A) ∪ [(B ∪ C) − A].
8. Niech At = {x ∈ R : (x + 2t)(x − 1t ) ­ 0}. Wyznaczyć zbiory
[
At oraz
t∈N+
\
At .
t∈N+
9. Zaznaczyć w układzie współrzędnych zbiory
9.1. A1 , A3 ,
9.2. A1 , A2 ,
∞
[
At ,
t=1
\
∞
\
At , jeśli At = {(x, y) ∈ R2 : y ­ |x + t| − t}.
t=1
An , jeśli An = {(x, y) ∈ R2 :
1
n2 (|x|
− n) ¬ y ¬ 0}.
n∈N+
9.3. A1 , A3 ,
[
n∈N+
An ,
\
An , jeśli An = {(x, y) ∈ R2 : (x − n)2 + y 2 = n2 }.
n∈N+
10. Czy dana funkcja jest różnowartościowa? Czy jest ’na’ ?
10.1. f : R × R → R, f (x, y) = (x + 3)(5 − y 2 ). Opisać i naszkicować f −1 (f (A)) dla A = (−∞, −3] × {−4}.
x + y2 − 3
10.2. f : R2 → R, f (x, y) =
. Wyznaczyć f ([3, 5) × {2}). Opisać i narysować zbiór f −1 (R+ ).
y2 + 1
10.3. f : R → R2 , f (x) = (x2 , (x + 1)2 ). Wyznaczyć f (R+ ), f −1 ([1, 9)2 ).
10.4. f : R2 → R, f (x, y) = max{x, y}. Wyznaczyć f ((1, 4) × [−1, 3)). Opisać i narysować zbiór f −1 ({3}).
−1 ((−∞, 0i).
10.5. f : R2 → R, f (x, y) = (sin x + 1 + y) · y 2 . Wyznaczyć f (h− π4 , 3π
4 ) × {1}). Narysować zbiór f
11. Sprawdzić, czy dla f : R → R, f (x) = x(x+2), A = (−3, 0] jest spełniona równość f −1 (f (A)) = f (f −1 (A)).
12. Sprawdzić czy relacja jest relacją równoważności w zbiorze X.
Jeśli tak, wyznaczyć klasę abstrakcji podanego elementu.
12.1. X = R+ , mRn ⇔ x−y
12.2. X = Q, xρy ⇔ ∃n ∈ N 2n (x − y) ∈ Z, x = 0
xy ∈ Z
12.3. X = R+ , xρy ⇔ x12 − y12 ∈ Z, x = 12 12.4. X = R2 , (x1 , y1 )ρ(x2 , y2 ) ⇔ x1 + y2 = x2 + y1
12.5 X = R+ , x ∼ y ⇔ xy ∈ Q, x = π
12.6. X = N, nρm ⇔ 3|(n3 − 4m).
13. Czy działanie ◦ w zbiorze X jest przemienne, łączne? Czy ma element neutralny?
Dla jakich elementów zbioru X istnieją elementy odwrotne?
p
2xy
12.1. X = R+ , x ◦ y = xy+2x+2y
12.2. X = R, x ◦ y = x2 + y 2 12.3. X = R, x ◦ y = 16 (3x + 3y − 9xy + 1)
1