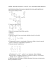Algebra liniowa, WNE, 2016/2017 ćwiczenia 19

Algebra liniowa, WNE, 2016/2017
ćwiczenia 19. – rozwiązania
13 grudnia 2016
1. Niech W = lin((0, 1, 2, 1), (2, 1, −6, −1)). Znaleźć bazę podprzestrzeni W ⊥ w przestrzeni R4 .
Rozwiązanie: W ⊥ to przestrzeń rozwiązań jednorodnego układu równań:
0 1 2
1
1 0 −4 −1
→
,
2 1 −6 −1
0 1 2
1
czyli baza to {(4, −2, 1, 0), (1, −1, 0, 1)}.
2. Niech W będzie podprzestrzenią przestrzeni R4 opisaną układem równań:
(
x1 + 2x2 − x3 + x4 = 0
x1 + 3x2 + x3 − x4 = 0
oraz niech Wt = lin((2, 5, 0, 0), (t+2, 4+3t, −2+t, (t−2)2 )). Dla jakich wartości parametru t ∈ R zachodzi:
• Wt ⊆ W ⊥ ?
• Wt = W ⊥ ?
Rozwiązanie: Baza W to {(5, −2, 1, 0), (−5, 2, 0, 1)}, czyli równania opisujące W ⊥ to
(
5x1 − 2x2 + x3 = 0
−5x1 + 2x2 + x4 = 0
Aby Wt ⊆ W ⊥ wektory (2, 5, 0, 0), (t + 2, 4 + 3t, −2 + t, (t − 2)2 ) muszą spełniać te równania. Pierwszy
rzeczywiście zawsze spełnia natomiast rozważając drugi, otrzymujemy układ równań:
(
5(t + 2) − 2(4 + 3t) − 2 + t = 0
−5(t + 2) + 2(4 + 3t) + (t − 2)2 = 0
pierwsze równanie jest tautologią, natomiast drugie daje: t2 − 3t + 2 = 0, co daje rozwiązania t = 1, 2.
Czyli dla t = 1 lub t = 2 zachodzi Wt ⊆ W ⊥ .
Aby Wt = W ⊥ muszą się zgadzać jeszcze wymiary, to znaczy dim Wt = 2, czyli wektory (2, 5, 0, 0), (t +
2, 4 + 3t, −2 + t, (t − 2)2 ) muszą być liniowo niezależne, co nie jest prawdą w przypadku t = 2 i jest w
przypadku t = 1. Więc ostatecznie Wt = W ⊥ wtedy i tylko wtedy, gdy t = 1.
3
3. W
ze standardowym iloczynem skalarnym rozważmy wektory: α = (−1, 2, 2), β = (−1 +
√ R √
√ przestrzeni
2 3, 2 + 2 3, 2 − 3), γ = (2, 1, t). Obliczyć kąt między wektorami α i β oraz określić dla jakich wartości
parametru t ∈ R kąt między wektorami α i γ wynosi 120◦ .
Rozwiązanie: cos(α, β) =
−1
2
= cos(α, γ) =
√2t
,
3· 5+t2
hα,βi
||α||·||β||
=
9
3·6
czyli t = −
q
= 21 , czyli szukany kąt to 60◦ .
45
7 .
4. Obliczyć współrzędne wektora (1, 3, 4) w bazie ortogonalnej (2, 2, −1), (2, −1, 2), (−1, 2, 2).
Ponieważ jest to baza ortogonalna, to współrzędne liczy się stosunkowo prosto: pierwsza to
4
7
13
9 , druga to 9 , a trzecia 9 .
1
h(1,3,4),(2,2,−1)i
h(2,2,−1),(2,2,−1)i
=
5. Niech W = lin((1, 1, 2, 1), (2, 3, 1, 3), (3, 5, 0, 5)) oraz V dana jako przestrzeń rozwiązań układu równań:
(
x1 + x2 − x3 + 2x4 = 0
−x1 + x2 + 2x3 − x4 = 0
będą podprzestrzeniami przestrzeni R4 ze standardowym iloczynem skalarnym. Znaleźć bazy ortogonalną
przestrzeni W i ortonormalną przestrzeni V .
W pierwszym przypadku stosujemy po prostu ortogonalizację Grama-Schmidta:
w1 = (1, 1, 2, 1)
w2 = (2, 3, 1, 3) −
w3 = (3, 5, 0, 5) −
10
1
h(1, 1, 2, 1), (2, 3, 1, 3)i
(1, 1, 2, 1) = (2, 3, 1, 3) − (1, 1, 2, 1) = (4, 11, −13, 11)
h(1, 1, 2, 1), (1, 1, 2, 1)i
7
7
h(1, 1, 2, 1), (3, 5, 0, 5)i
h(4, 11, −13, 11), (3, 5, 0, 5)i
(1, 1, 2, 1) −
(4, 11, −13, 11) =
h(1, 1, 2, 1), (1, 1, 2, 1)i
h(4, 11, −13, 11), (4, 11, −13, 11)i
13
122
1
2
(1, 1, 2, 1) −
(4, 11, −13, 11) = (8, 22, −26, 22) − (4, 11, −13, 11) = (0, 0, 0, 0)
7
427
7
7
A więc dim W = 2 i baza ortogonalna to np. {(1, 1, 2, 1), (4, 11, −13, 11)}.
Tymczasem bazą V jest np. {(−3, 1, −2, 0), (−3, 0, −1, 1)}. Ortogonalizujemy:
= (3, 5, 0, 5) −
v1 = (−3, 1, −2, 0)
v2 = (−3, 0, −1, 1) −
11
h(−3, 1, −2, 0), (−3, 0, −1, 1)i
(−3, 1, −2, 0) = (−3, 0, −1, 1) − (−3, 1, −2, 0) =
h(−3, 1, −2, 0), (−3, 1, −2, 0)i
14
=
1
(−9, −11, 8, 14).
14
1
Jeszcze trzeba znormalizować, czyli baza ortonormalna w V to { √114 (−3, 1, −2, 0), √462
(−9, −11, 8, 14)}.
2