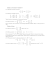Grupa obrotów

Grupa obrotów
- wszystkie możliwe obroty o dowolne
kąty wokół osi przechodzących przez
środek kuli
+
inaczej O (3) – grupa obrotów właściwych
- grupa symetrii kuli,
R
- grupa ciągła
- każdy obrót określa się przez podanie osi
Cl (α)
- obrót Cl (α)
α
l,
i kąta obrotu
α
defniuje się przez podanie wektora
= (αx,αy,αz )
wzdłuż osi l, i o długości
α = α x2 + α y2 + α z2 ≤ 2π
R x Ci = Rh
tzn. dodanie inwersji do R, tworzy tzw. pełną grupę ortogonalną
każda skończona grupa punktowa jest podgrupą grupy
ortogonalnej
obroty o nieskończenie małe kąty
obrót o dowolny kąt - ciąg obrotów o dowolnie małe kąty φ
dla „małego” φ
(X)
x' = x + x × ϕ
(tu
X oznacza dowolny wektor
r o 3 składowych x,y,x)
gdzie φ można złożyć z 3 obrotów o kąty φx , φy , φz ,
wokół osi – odpowiednio – x, y, z
zobaczmy jak zmienia się funkcja F(x,y,z) (różniczkowalna) przy
„nieskończenie małym obrocie” o
φ
D(ϕ ) F ( x, y, z ) = F (x') =
F ( x + zϕ y − yϕ z , y − zϕ x + xϕ z , z + yϕ x − xϕ y )
rozkładając w szereg Taylora i zachowując tylko wyrazy liniowe
(Y)
D(ϕ ) F ( x, y, z ) = F ( x, y, z ) +
( zϕ y − yϕ z ) ∂∂Fx + ( xϕ z − zϕ x ) ∂∂Fy + ( yϕ x − xϕ y ) ∂∂Fz + ..
= (1 + iLϕ ) F ( x, y, z )
(pominąłem chwilowo dalsze wyrazy .. )
gdzie
L = −ix × ∇
(tu X = r)
jest (z dokładnością do stałej Plancka) operatorem momentu pędu –
a tu nazywa się operatorem nieskończenie małego obrotu
można dość łatwo pokazać, że pełne rozwinięcie (Y) daje
(i (Lϕ )) 2
(i (Lϕ ))n
D(ϕ ) = 1 + i (Lϕ ) +
+ ... +
+ ... = ei ( Lϕ )
2
n!
(*L)
widzimy związki:
• grupa translacji - operator pędu
• grupa obrotów - operator momentu pędu
związek z macierzami Pauliego i spinem
niech kula ma promień jednostkowy i środek w (0,0,0),
każdemu punktowi P kuli przyporządkowujemy pewien punkt
płaszczyzny P’ o współrzędnych (ζη) lub ( z = ζ + i η ) – jako
liczbę zespoloną
każdy obrót kuli przeprowadzający punkt P w M przeprowadza
P’ w M’ tzn. (ζη) w (ζ’η’) ;
jest to pewne przekształcenie płaszczyzny
można pokazać, że
z' =
αz + β
γz + δ
(s1)
z zespolonymi współczynnikami, zależnymi od składowych wektora
obrotu
ϕ
to przekształcenie płaszczyzny można opisać za pomocą
macierzy unitarnej u (gdyż dwie składowe: ζ, η )
α β
u=
γ δ
i det | u | = 1,
uwaga: unitarność
UT = U-1 tzn. UUT = I
(s2)
każdemu obrotowi można więc przyporządkować macierz unitarną,
o dim=2, macierze te tworzą grupę - tzw. grupę unitarną U
istnieje odpowiedniość między U a grupą sferyczną – ale nie
izomorfizm gdyż, jednemu obrotowi kuli odpowiadają dwa
przekształcenia płaszczyzny u oraz -u
jądrem homomorfizmu jest tu podgrupa składająca się z 2 macierzy
jednostkowej, I, oraz -I
(rzeczywiście, z (s1) i (s2) wynika, źe I i -I prowadzą do tego samego Z’ )
macierz u odpowiadająca obrotowi
ma postać (bez dowodu)
ϕ
o składowych ϕx , ϕy , ϕz
[
]
u (ϕ ) = exp i (σ xϕ x + σ yϕ y + σ zϕ z ) / 2 = exp[i (σϕ ) / 2]
gdzie
σx =
σi
- macierze Pauliego
0 1
0 −i
1 0
, σy =
, σz =
,
i 0
1 0
0 −1
+
(pamiętamy, że obrotowi w O (3) odpowiada
ei(Lφ)
)
korzystając z (*L) można pokazać, że
u (ϕ ) = I cos
ϕ
2
+i
(σϕ )
ϕ
sin
ϕ
2
(wyrazy o potęgach parzystych, korzystając z własności macierzy σi ,
zwijają się do cos , a nieparzyste do sin )
obrotom wokół osi Z odpowiada:
e iϕ / 2
u (ϕ z ) = I cos + iσ z sin =
2
2
0
ϕ
ϕ
0
e − iϕ / 2
σi2 = 1,
stąd widać, że obroty o
znakiem
ϕ
i
ϕ +2π
mają macierze różniące się
kontynuując związki:
• grupa unitarna - operator „spinu”
Grupa SU(2)
===========
 a
− b *

grupa macierzy unitarnych postaci
b
a * 
z własnością
aa* + bb* = 1, a,b – zespolone
istnieje związek między SU(2) a O+(3) – pełną grupą obrotów
właściwych
fragment dowodu:
1. przypomnijmy macierze Pauliego
0 1 
σx = 
,
1
0


0
i
σy = 
,
0
−
i


− 1 0
1
σz = 
0
2. zdefiniujmy macierz
 −z
 
r ⋅ σ = xσ x + yσ y + zσ z = 
 x − iy
x + iy 
z 
macierz ta jest hermitowska o znikającym śladzie
3. dokonajmy transformacji podobieństwa na rσ za pomocą u ∈SU(2)
 
u (r ⋅ σ )u −1
można pokazać (na ćwiczeniach), że wynik jest też macierzą
hermitowską o Tr = 0, zatem musi odpowiadać mu macierz typu
 − z ' x'+iy '  
 x'−iy '
 = r 'σ ,
z
'


dla r’ = (x’, y’, z’)
zatem powyższej transformacji podobieństwa za pomocą u odpowiada
jakaś Ru , która w O+(3) odpowiada jakiemuś obrotowi
przeprowadzającemu wektor r w wektor r’ .
Odwzorowanie SU(2) -> O+(3) jest homomorficzne
1 0 − 1 0 
jądrem tego homomorfizmu są dwie macierze 
,  0 − 1
0
1

 

każdemu
Ru ∈ O+(3)
odpowiadają dwie:
u, -u ∈SU(2)
def.
Grupa podwójna (grupy punktowej)
zbiór macierzy SU(2) odpowiadających operacjom danej grupy
punktowej będącej podgrupą O+(3)