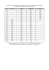zestaw nr 26.

26. Modele wartości pieniądza w czasie. Współczynnik
akumulacji kapitału. Kapitalizacja okresowa, kapitalizacja
ciągła. Wartość bieżąca, wartość przyszła. Pojęcia kredytu,
renty, renty wieczystej, zadłużenia bieżącego.
1
Podstawowe pojęcia i oznaczenia.
Kapitał początkowy (P) - wartość początkowa; kwota, która została wpłacona na początku
inwestycji.
Kapitał końcowy (F) - wartość końcowa; kwota, jaką uzyskamy po pewnym czasie inwestycji
(lub na jej koniec).
Odsetki (I) - zysk; różnica pomiędzy wartością końcową a początkową.
I =F −P
Stopa procentowa (i) - stosunek odsetek do kapitały początkowego.
i=
F −P
I
=
P
P
Oprocentowanie - generowanie zysku przez ustalony kapitał.
Okres oprocentowania - najkrótszy przedział czasu, po którym zostaną dopisane odsetki.
Kapitalizacja (odsetek) - dołączanie odsetek do kapitału.
Oprocentowanie zgodne - gdy okres stopy procentowej pokrywa się z okresem oprocentowania.
Oprocentowanie niezgodne - gdy okres stopy procentowej i oprocentowania nie pokrywają się.
Oprocentowanie proste - opocentowaniu podlega wyłącznie kapitał początkowy.
Oprocentowanie składane - oprocentowaniu podlega zarówno kapitał początkowy jak i wygenerowane w czasie inwestycji odsetki.
Dyskontowanie - działanie odwrotne do oprocentowania; wyznaczanie wartości początkowej na
podstawie wartości końcowej.
Dyskonto - kwota o jaką trzeba pomniejszyć wartość końcową aby otrzymać wartość początkową.
2
Współczynnik akumulacji.
Niech [0, T ] będzie czasem inwestycji jednej jednostki kapitału T , T ≥ 0.
Niech a(t) ≥ 0 oznacza wartość przyszłą tego kapitału w momencie t ∈ [0, T ].
Funkcję a : t → a(t) nazywamy funkcją akumulacji jednej jednostki kapitału.
Dla ustalonego t ∈ [0, T ] wartość a(t) nazywamy t-okresowym współczynnikiem akumulacji.
Wówczas, gdy inwestycją będzie kapitał o wartości P, to jego wartość przyszła w czasie t ∈ [0, T ]
wyrazi się wzorem
Ft = P · a(t)
Oczywiście F0 = P .
Analogicznie dla ustalonego t ∈ [0, T ] wartość a(t)−1 nazywamy t-okresowym współczynnikie
dyskontowania. Wtedy dla kapitału Ft jego wartość początkowa wyraża się wzorem
P = Ft · a(t)−1
Własności funkcji akumulacji:
1. a(0) = 1
2. a jest funkcją rosnącą. Gdyby funkcja przyjmowała wartości mniejsze przy wzroście t, to
generowałaby ujemne odsetki. Od strony matematycznej jest to możliwe natomiast od strony
funansowej takimi przypadkami nie będziemy się zajmować.
1
3. Jeżeli generowane odsetki będą gromadzić się w sposób ciągły, to funkcja akumulacji też
będzie ciągła. Jeżeli odsetki będą gromadzić się w sposób skokowy zależnie od okresu oprocentowania, to funcja akumulacji będzie w tych punktach nieciągła, a dokładnie będzie ciągła
z prawej strony.
3
Oprocentowanie zgodne.
Załóżmy, że czas oprocentowania składa się z n podokresów będących okresami oprocentowania
oraz, ze okres stopy procentowej pokrywa się z okresem oprocentowania.
3.1
Oprocentowanie proste
Kapitalizację w której podstawą naliczania odsetek jest tylko kapitał początkowy nazywamy oprocentowaniem prostym (kapitalizacją prostą). W kapitalizacji prostej odsetki nie podlegają oprocentowaniu.
Zasada oprocentowania prostego stosowana jest w transakcjach bankowych krótkoterminowych do
jednego roku albo też w umowach poza sferą bankową.
Zatem jeżeli mamy oprocentowanie roczne i stopę procentową roczną, to po roku otrzymamy
P · i odsetek, po dwóch latach P · 2i itp.
W efekcie tego mamy po n latach:
Kapitał końcowy:
Fn = P (1 + ni)
Funcja akumulacji:
a(n) = 1 + ni
Przykład 1. Jaka kwota w oprocentowaniu prostym na 40% rocznie pozwoli po 5 latach uzyskać
kwotę 30 mln złotych?
30 = P (1 + 5 · 0, 4)
30
= 10 (mln zł)
3
Zatem, jakbyśmy teraz zainwestowali 10 mln zł to po 5 latach mielibyśmy 30 mln zł.
P =
3.2
Oprocentowanie składane
Model oprocentowania, w którym odsetki wygenerowane po każdym okresie oprocentowania podlegają kapitalizacji nazywamy oprocentowaniem składanym.
Stosowany jest z reguły w inwestycjach średnioterminowych (1−5 lat) i długoterminowych (powyżej
5 lat).
Jeżeli procent jest dopisywany do rachunku corocznie, to po jednym roku pieniądze złożone na
rachunku zostają pomnożone przez 1 + i. Po drugim roku czynnik ten rośnie do (1 + i)2 .
W efekcie tego mamy po n latach:
Kapitał końcowy:
Fn = P (1 + i)n
Funcja akumulacji:
a(n) = (1 + i)n
4
Oprocentowanie niezgodne.
W dotychczasowych rozważaniach odsetki dopisywaliśmy do kapitału na końcu kolejnych lat. Jednak większość banków podaje stopę procentową roczną a odsetki nalicza i wypłaca częściej - co
kwartał, co miesiąc. W takiej sytuacji korzystamy z modelu oprocentowania niezgodnego.
Oprocentowanie jest niezgodne jeżeli okres stopy procentowej nie jest równy okresowi kapitalizacji. Możemy podzielić takie sytuacje na dwie klasy:
2
1. Kapitalizację w podokresach, gdy okres stopy procentowej jest całkowitą wielokrotnością
okresu kapitalizacji, np. roczna stopa procentowa i kapitalizacja miesięczna.
2. Kapitalizację w nadokresach, gdy okres kapitalizacji jest całkowitą wielokrotnością okresu
stopy procentowej, np. roczna stopa procentowa i kapitalizacja 4-letnia.
Niech i oznacza teraz roczną stopę procentową. Niech k oznacza stosunek:
k=
okres stopy procentowej
okres kapitalizacji
W przypadku oprocentowania niezgodnego odsetki przypadające na jeden okres kapitalizacji wyznacza się na podstawie stopy, której okres pokrywa się z okresem kapitalizacji. Nazywamy ją
stopą podokresową (dostosowaną, względną) i oznaczamy przez ik . Wyznaczamy ją ze wzoaru:
i
k
W takim przypadku stopę i nazywamy nominalną stopą procentową.
Wyznaczenie wartości przyszłej jest tu analogiczne do przypadku kapitalizacji zgodnej. Jedynie w
miejscu stopy i używa się stopy podokresowej ik , zaś liczbę okresów kapitalizacji łatwo wyznaczyć
można jako:
mk = n · k
ik =
gdzie n - liczba okresów stopy nominalnej mieszcząca się w czasie oprocentowania inwestycji.
Zgodnie z tym wartość przyszła kapitału P po mk okresach kapitalizacji wynosi odpowiednio:
dla oprocentowania prostego
Fmk = P (1 + mk ik )
dla oprocentowania składanego
Fmk = P (1 + ik )mk
Przykład 2. Obliczyć wartość przyszłą kapitału w wysokości 1000 zł po półtora roku w modelu
składanej kapializacji kwartalnej przy nominalnej stopie 8%.
Z treści zadania wynika, że:
P = 1000
i = 0, 08
k=4
n = 1, 5
Obliczmy:
0, 08
= 0, 02
4
mk = 1, 5 · 4 = 6
ik =
W konsekwencji mamy:
F6 = 1000(1 + 0, 02)6 = 1126, 16 (zł)
5
Dyskontowanie
Dyskontowanie dzielimy na dyskontowanie matematyczne i handlowe.
1. Dyskontowanie matematyczne (rzeczywiste) - wyznaczanie wartości początkowej P na podstawie znanej wartości kapitału końcowego F przy ustalonej stopie i, n - czas oprocentowania.
Oblicza się je ze wzoru:
ni
F
=F·
- kapitalizacja prosta
1 + ni
1 + ni
F
1
D =F −P =F −
= F · (1 −
) - kapitalizacja składana
(1 + i)n
(1 + i)n
D =F −P =F −
2. Dyskontowanie handlowe - wyznaczanie wartości początkowej P na podstawie znanego kapitału końcowego F przy ustalonej stopie dyskontowej d, n - czas oprocentowania.
Oblicza się je ze wzoru:
Dh = F · d · n - kapitalizacja prosta
P = F − D = F (1 − d)n - kapitalizacja składana
3
6
Kapitalizacja ciągła
Rok można podzielić na coraz mniejsze okresy stosując kapitalizację miesięczną, tygodniową, dzienną a nawet dopisywać odsetki co minutę lub co sekundę. Dalsze zmniejszanie długości okresu prowadzi w efekcie do kapitalizacji ciągłej.
Kapitalizacją ciągła to graniczny przypadek złożonej kapitalizacji w podokresach tzn. gdy liczba
okresów kapitalizacji k w ustalonym okresie n dąży do nieskończoności. Inaczej mówiąc mamy do
czynienia z sytuacją, gdy odsetki kapitalizowane są w każdym momencie czasu.
Stąd otrzymujemy:
i ki ni
i nk
= lim P 1 +
= P eni
lim P 1 +
n→∞
k→∞
k
k
W efekcie tego mamy po n latach:
Kapitał końcowy:
Fn = P eni
Funcja akumulacji:
a(n) = eni
7
Renty.
7.1
Definicja renty.
Renta (ang. annuity) jest zdefiniowana jako ciąg płatności dokonywanych w równych odstępach
czasu. Płatności, które składają się na renty nazywane są ratami.Okres pomiędzy kolejnymi ratami
nazywa się okresem bazowym.
Momentem początkowym renty jest t = 0, natomiast momentem końcowym renty jest koniec
okresu, za który płacona jest ostatnia rata.
Rentę charakteryzują następujące elementy:
1. Liczba rat
2. Długość okresu bazowego.
3. Wysokość rat.
4. Moment pierwszej płatności.
5. Stopa procentowa okresu bazowego.
6. Zasady naliczania odsetek w podokresach.
Różne klasy rent:
1. renta prosta - okres kapitalizacji pokrywa się z okresem bazowym
renta uogólniona - okres kapitalizacji i okres bazowy nie pokrywają się
2. renta czasowa - renta o skończonej liczbie rat
renta wieczysta - renta o nieskończonej liczbie rat
3. renta płatna z góry - raty płacone na początku okresu bazowego
renta płatna z dołu - rata płacona na koniec okresu bazowego
7.2
Podstawowe wzory.
Wprowadźmy następujące oznaczenia:
P - wartość początkowa renty
F - wartość końcowa renty
Cj - rata płatna w momencie j, j = 1, 2, . . .
C - wielkość raty w przypadku równych płatności, tj. Cj = C dla każdego j = 1, . . . , n
i - stopa procentowa okresu bazowego
Kapitalizacja prosta odsetek, renta płatna z dołu.
Rozważmy ciąg skończony wpłat (Cj )nj=1 dokonywanych z dołu. Niech i będzie stopą procentową
4
dostosowaną do okresu bazowego.
Wartość przyszła ciągu wpłat po n płatnościach wynosi:
F =
n
X
Cj (1 + (n − j)i)
j=1
W przypadku równych rat wartość przyszła ciągu wpłat po n płatnościach wynosi:
n−1 ·i
F =C ·n· 1+
2
Natomiast wartość początkowa:
P =F·
1
1 + ni
Kapitalizacja prosta odsetek, renta płatna z góry.
Rozważmy ciąg skończony wpłat (Cj )nj=1 dokonywanych z góry. Niech i będzie stopą procentową
dostosowaną do okresu bazowego.
Wartość przyszła ciągu wpłat po n płatnościach wynosi:
F (+1) =
n
X
Cj (1 + ((n + 1) − j)i)
j=1
W przypadku równych rat wartość przyszła ciągu wpłat po n płatnościach wynosi:
n+1 ·i
F (+1) = C · n · 1 +
2
Natomiast wartość początkowa:
P (+1) = F (+1) ·
1
1 + ni
Kapitalizacja złożona odsetek, renta płatna z dołu.
Rozważmy ciąg skończony wpłat (Cj )nj=1 dokonywanych z dołu. Niech i będzie stopą procentową o
okresie oprocentowania równym okresowi bazowemu oraz niech okres bazowy pokrywa się z okresem
kapitalizacji.
Wartość przyszła ciągu wpłat po n płatnościach wynosi:
F =
n
X
Cj (1 + i)n−j
j=1
W przypadku równych rat wartość przyszła ciągu wpłat po n płatnościach wynosi:
(1 + i)n − 1
i
F =C·
Natomiast wartość początkowa:
P =C·
1 − (1 + i)−n
i
Kapitalizacja złożona odsetek, renta płatna z góry.
Rozważmy ciąg skończony wpłat (Cj )nj=1 dokonywanych z góry. Niech i będzie stopą procentową o
okresie oprocentowania równym okresowi bazowemu oraz niech okres bazowy pokrywa się z okresem
kapitalizacji.
Wartość przyszła ciągu wpłat po n płatnościach wynosi:
F (+1) =
n
X
Cj (1 + i)(n+1)−j
j=1
W przypadku równych rat wartość przyszła ciągu wpłat po n płatnościach wynosi:
F (+1) = C ·
(1 + i)n − 1
· (1 + i)
i
5
Natomiast wartość początkowa:
P (+1) = C ·
1 − (1 + i)−n
· (1 + i)
i
Renta wieczysta.
Renta wieczysta jest wypłacana nieskończenie długo. Nie można wyznaczyć jej wartości przyszłej.
P =
P (+1) =
8
R
i
R
· (1 + i)
i
Kredyt.
Zaciągnięty dług, inaczej kredyt, oznaczamy przez S. Dług ten jest najczęściej spłacany w częściach
zwanych ratami łącznymi lub płatnościami.
Mówimy, że dług został spłacony jeżeli w określonym przedziale czasu suma spłaconych rat jest
równa zaciągniętej pożyczce wraz z odsetkami z tytułu "użytkowania" wypożyczonego kapitału.
Przyjmuje się, że do rozliczeń długów krótkoterminowych stosuje się model kapitalizacji prostej,
a do rozliczeń długów średnio- i długoterminowych stosuje się model kapitalizacji złożonej z dołu.
Przyjmijmy oznaczenia:
S - wartość początkowa długu
N - ilość rat
i - stopa okresu bazowego
Rn - n-ta spłata długu
Tn - część kapitałowa (procentująca) długu spłacana w n-tej racie
In - odsetki spłacane w n-tej racie
Sn - reszta długu pozostała po spłaceniu n-tej raty
I - suma wszystkich odsetek
Ciąg (Rn ), (Tn ), (In ), (Sn ), I określa plan spłaty długu. Natomiast każda rata łączna zawiera
dwa składniki: ratę kapitałową i odsetki, tzn. Rn = Tn + In dla n = 1, . . . , N .
8.1
Spłata długów krótkoterminowych
Rozważmy dług o wartoścy S w momencie t = 0. Spłacamy go ratami Rn . Załóżmym, że od długu
naliczone są odsetki proste przy stopie okresu bazowego i.
Dług o wartości S w momencie t = 0 jest równiważmy w momencie t = j ciągowi rat Rn płatnych
w momencie n = 1, . . . , N jeżeli kapitały wzajemnie sobie przekazane przez wierzyciela i dłużnika
są równoważne w momencie j.
Fakt spłacenia długu S ratami R1 , . . . , RN oznacza zachodzenie równości:
S(1 + ji) =
j
X
Rn [1 + (j − n)i] +
n=1
N
X
n=j+1
Rn
1
1 + (n − j)i
dla dyskonta matematycznego, lub
S(1 + ji) =
j
X
Rn [1 + (j − n)i] +
n=1
N
X
Rn [1 + (j − n)i]
n=j+1
dla dyskonta handlowego.
Wartość zadłużenia po spłacie n rat zaktualizowana na moment t=0 wynosi:
dla dyskonta matematycznego:
(
Pn
jeżeli1 ≤ n ≤ j
S − l=1 Rl 1+(j−l)i
0
1+ji
Pj
Pn
Sn =
1
S − l=1 Rl 1+(j−l)i
−
R
dla
n>j
l=j+1 l (1+ji)(1+(l−j)i)
1+ji
6
dla dystonta handlowego:
Sn0 = S −
n
X
Rn
l=1
1 + (j − l)i
1 + ji
Spłata długu w równych ratach łącznych:
1. Dla dyskonta matematycznego otrzymujemy:
1 + ji
PN
R = S · Pj
n=1 (1 + (j − n)i) +
1
n+j+1 1+(n−j)i
Natomiast rozkład raty na część kapitałową i odsetkową przedstawia się następująco:
T =
2(S(1 + N i) − RN )
(N − 1)N i
I =R−T
2. Dla dyskonta handlowego:
R=
S
1 + ji
·
N 1 + (j − N2+1 · i)
Rozkład raty na część kapitałową i odsetkową są takie same jak w dyskoncie matmatycznym.
I =R−T
Szczególnym przypadkiem rat umarzających dług krótkoterminowy są tzw. raty kupieckie.
Wyrażają się one wzorem:
1 + Ni
S
·
R=
N 1 + N 2−1 · i
Rata kupiecka składa się tylko z raty kapitałowej, czyli T = R oraz I = 0. Odsetki od długu są
umarzane przez odsetki od raty.
8.2
Spłata długów średnio- i długoterminowych.
W modelu kapitalizacji złożonej moment aktualizacji nie jest istatny. Dlatego mamy:
S(1 + i)N =
N
X
Rn (1 + i)N −n
n=1
W tym modelu występują następujące zależności:
Sn = Sn−1 (1 + i) − Rn
In = Sn−1 · i
Rn = Tn + In
PN
Tn = Sn−1 − Sn oraz n=1 Tn = S
Spłata długu w równych ratach:
Niech dany będzie ciąg o stałych płatnościach w wysokości R w równych odstępach czasu. Umarza
on dług S jaki powstał w momencie t = 0 przy stopie okresu bazowego i.
Wysokość takiej raty wynosi:
S(1 + i)N · i
R=
(1 + i)N − 1
Przykład 3. Dług 20 jp ma zostać spłacony w czterech ratach rocznych. Wiemy, ze części kapitałowe wynoszą: T1 = 5 jp, T3 = 8jp, T4 = 3 jp. Roczna stopa procentowa wynosi 15%, kapitalizacja
złożona. Ułóż plan spłaty kredytu.
T2 = 20 − 5 − 8 − 3 = 4
S1 = 20 − 5 = 15
I1 = 20 · 0, 15 = 3
R1 = 5 + 3 = 8
S2 = 20 − 5 − 4 = 11
itd.
7
n
1
2
3
4
Sn−1
20
15
11
3
Rn = Tn +In
8
6,25
9,65
3,45
In = Sn−1 · i
3
2,25
1,65
0,45
Tn
5
4
8
3
8
Sn = S −
15
11
3
0
PN
n=1
Tn