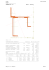Momenty bezwładności figur płaskich

MOMENTY BEZWŁADNOŚCI
FIGUR PŁASKICH
Przekroje poprzeczne prętów, wałów i belek – figury płaskie,
charakteryzujące się następującymi parametrami:
– polem powierzchni przekroju
[mm2, cm2, m2],
– położeniem środka ciężkości przekroju,
– momentami statycznymi
[cm3, m3],
– momentami bezwładności
[cm4, m4].
Definicja momentu statycznego w w
układzie osi X i Y:
Sx   ydA, Sy   xdA
A
A
W zależności od położenia przekroju względem osi układu współrzędnych mogą przyjmować wartości
dodatnie i ujemne.
Definicja momentu statycznego
Wykorzystując znane ze statyki pojęcie środka sił, dla środka
ciężkości można napisać:
Sx  yc A,
Sy  xc A.
Korzystając z tych zależności, współrzędne środka ciężkości
figury płaskiej można obliczyć ze wzoru:
Sy
S
xc  , yc  x .
A
A
Środek ciężkości przekrojów złożonych –podział przekroju na
figury proste.
n
xc 
 A i xi
i1
n
 Ai
i1
n
,
yc 
 A i yi
i1
n
 Ai
,
i1
Ai – pola powierzchni figur prostych, xi, yi – współrzędne środków ciężkości poszczególnych figur prostych.
09 Momenty bezwładności figur płaskich.doc
104
PRZYKŁAD
Określić położenie środka ciężkości figury przedstawionej na rysunku.
Przekrój podzielono na trzy prostokąty
o następujących polach powierzchni:
A1 = 1  1 = 1 cm2,
A2 = 2  5 = 10 cm2,
A3 = 2  2 = 4 cm2.
Współrzędne środka ciężkości całej figury wynoszą
A1x1  A 2 x 2  A 3 x 3 1 1,5  10  3  4  5

 3,43 cm,
A1  A 2  A 3
1  10  4
A y  A 2 y 2  A 3 y 3 1  1,5  10  3,5  4  5
yc  1 1

 3,77 cm.
A1  A 2  A 3
1  10  4
xc 
Momenty bezwładności
Definicja momentów bezwładności:
– osiowe momenty bezwładności
Jx   y 2 dA, Jy   x 2 dA,
A
A
– biegunowy moment bezwładności
J0   2dA   x 2  y 2 dA  Jx  Jy,

A

A
– moment dewiacyjny (zboczenia, odśrodkowy)
Jxy   xydA .
A
Momenty osiowe oraz moment biegunowy są
zawsze dodatnie, natomiast
moment dewiacyjny może być dodatni lub ujemny.
09 Momenty bezwładności figur płaskich.doc
105
Momenty bezwładności figur złożonych są sumą momentów
bezwładności prostych figur składowych. Figura złożona może
składać się z figur „pełnych” oraz „pustych”. Przy sumowaniu
momentów bezwładności figury „puste” uważa się za figury z
ujemnymi polami powierzchni.
PRZYKŁAD
Figury złożone przedstawione na rysunku podzielić na figury proste.
Podział
figury złożonej
na figury proste
(jeden z możliwych
do zastosowania
podziałów figury).
Twierdzenie Steinera
Twierdzenie Steinera umożliwia obliczanie momentów
bezwładności figur płaskich
względem
osi
równolegle
przesuniętych w stosunku do
osi centralnych (osi przechodzących przez środek ciężkości przekroju).
Dla figury płaskiej o powierzchni A, obliczyć momenty bezwładności względem osi X–Y, równolegle przesuniętych w stosunku do osi centralnych (środkowych) X0–Y0 o odcinki a i b.
Na podstawie definicji momentu bezwładności moment osiowy względem osi X dla y1 = y + a wyraża wzór:
Jx   y1dA 
A
 y  a
2
A
dA   y 2dA  2a  ydA  a2  dA  Jx 0  Aa2.
A
09 Momenty bezwładności figur płaskich.doc
A
A
106
W powyższym równaniu całka
 ydA opisuje moment statycz-
A
ny, który względem osi centralnych jest równy zeru. W podobny
sposób określa się moment względem osi Y oraz moment dewiacyjny
Jy 
 x  b
2
A
Jxy 
dA  Jx 0  Ab2,
 x  ax  bdA  Jx 0 y 0
 Aab.
A
Wyprowadzone wyżej zależności noszą nazwę twierdzenia
Steinera.
Osiowy moment bezwładności figury płaskiej względem osi
równoległej odległej od środka ciężkości o określoną wartość
jest równy momentowi względem osi równoległej przechodzącej przez środek ciężkości figury, powiększonemu o iloczyn
powierzchni figury i kwadratu odległości między osiami.
Moment dewiacyjny figury płaskiej względem osi równolegle
przesuniętych jest równy momentowi dewiacyjnemu względem osi centralnych, powiększonemu o iloczyn powierzchni i
obu składowych równoległego przesunięcia.
Twierdzenie Steinera ma następująca postać matematyczną:
Jx  Jx 0  Aa2,
Jy  Jy 0  Ab2,
Jxy  Jx 0 y 0  Aab.
GŁÓWNE MOMENTY BEZWŁADNOŚCI
Osie przechodzące przez środek ciężkości przekroju – OSIE
CENTRALNE. Osie obrócone pod odpowiednim katem, powodującym wyzerowanie momentów dewiacyjnych – GŁÓWNE
OSIE BEZWŁADNOŚCI.
Momenty względem tych osi – GŁÓWNE MOMENTY BEZWŁADNOŚCI
09 Momenty bezwładności figur płaskich.doc
107
MOMENTY BEZWŁADNOŚCI DLA PRZEKROJU PROSTOKĄTNEGO
Momenty bezwładności względem osi centralnych XC–YC
Y
YC
dA = bdy
XC
C
h
y
dy
Osie
centralne
X
b
IXc   y 2dA 
A
h
2
2
 y b dy 
h

2
bh3
,
12
IYc 
hb3
,
12
IXc Yc  0
Momenty bezwładności względem osi X–Y
Y
dA
y
h
dy
Y
X
X
x
b
h
h 2
bh3
hb3
b
b2h2
b
IX   y dA   y b dy 
, IY 
, IXY   xydA    y b dy   y dy 
.
3
3
4
A
0
A
02
0 2
h
2
2
TWIERDZENIE STEINERA
2
IX  IXc
bh3 bh3 bh3
h
 A  


,
12
4
3
 2
IXcYc  IXY
2
IY  IYc
hb3 hb3 hb3
b
 A  


,
12
4
3
 2
bh b 2h2
hb
 A       0  (bh)

.
4
4
 2 2
09 Momenty bezwładności figur płaskich.doc
108
Przykład:
Dla trójkąta prostokątnego przedstawionego na rysunku
wyznaczyć momenty bezwładności względem osi X–Y oraz
osi centralnych X0–Y0.
Osie centralne
Wyznaczyć główne momenty bezwładności oraz ich położenie.
Osiowy moment bezwładności względem osi X:
b
Jx   y 2dA   y 2udy, u 
A
0
b
3
a
b  y y2dy  ab .
b
12
0
a
b  y ,
b
Jx  
Osiowy moment bezwładności względem osi Y:
a
Jy   x 2dA   x 2 tdx, t 
A
0
b
3
b
a  x  x 2dx  ba .
a
12
0
b
a  x ,
a
Jy  
Moment dewiacyjny wyznacza się po określeniu współrzędnych środka ciężkości powierzchni:
b
b
1
1 a2
a2b2
2
Jxy   xydA   xyudy, x  u,
Jxy   2 b  y  ydy 
.
2
20b
24
A
0
Momenty bezwładności względem osi centralnych (twierdzenia Steinera):
2
2
ab3 ab b2 ab3
ba3 ab a 2 ba3
b
a
Jx 0  J x  A   


, Jy 0  J y  A   


,
12
2 9
36
12
2 9
36
3
3
2 2
a 2b2
a 2b2
 a  b  a b
Jx0y0  Jxy  A   


.
24
18
72
 3  3 
Główne momenty bezwładności:
J1,2 
ab(a 2  b2 ) ab 4

a  b4  a 2b2 .
72
72
Osie główne
Położenie głównych centralnych osi bezwładności:
tg2o  
2Jx0y0
Jx0 Jy0
a 2b2
ab
  3 72 2  2 2  0.
ab ba
b a

12 12

Kąt o jest dodatni i wskazuje kierunek momentu J1.
09 Momenty bezwładności figur płaskich.doc
109
Momenty bezwładności figur prostych
Figura
Jx
Jy
bh3
J xo 
12
bh3
Jx 
3
hb 3
J yo 
12
hb 3
Jy 
3
bh3

36
hb 3

36
J xo
bh3
Jx 
12
Jx 

J xo
D 4

64
R
4
4
D4   8 

 

16  8 9 
 0,00686D 4 
 0,1098R 4
D 4 R 4
Jx 

128
8
J xo
hb 3
Jx 
12
Jy 

D 4

64
R
4
D 4 R 4
Jx 

256
16
4
D 4
Jy 

128

R 4
8
J xo yo  0
b 2h 2

4
J xy
b 2h 2
72
2 2
b h

24
J xo yo  
J xy
Jxy  0
J xy  0
J xo yo  0
J xy 
4
 
J xo  R 4  

 16 9 
 0,0549R 4
Jxy
Jx 
4
R
16
J xo y0 

R4
8
R4

8
4R 4

9
 0,0165R 4
09 Momenty bezwładności figur płaskich.doc
110
PRZYKŁAD
Dla figury płaskiej pokazanej wyznaczyć wartości centralnych momentów bezwładności.
3t
Y = Ys
1
Y1
2t
C1
X1
2
t
C2
2t
3'
7t
C'3
Y3 C
X3
Y4
4
X2
Y3
Xs
X3
3"
C"3
ys
5t
Y
2
t
X4
C4
X
Figura złożona zostaje podzielona na figury proste. Korzystając ze
wzorów na wyznaczanie środka ciężkości względem osi X-Y otrzymuje
się
6t 9t   6t 5t   2  1,5t  2 31 t   14t t  105t




6t   6t   2  1,5t   14t 
29t
2
ys
2
2
2
2
2
2
2
3
2
 3,62t ,
xs  0.
Osiowe momenty bezwładności wynoszą
Jx s
2
 6t  2t 3
2   t  6t 
2
2

 6t 9t  3,62t    
 6t 2 5t  3,62t   
5,38 t
 12 Figura 1
  12 Figura 2 1,38 t

 
 

2
3
3
3
t

t
1
   7t  2t 
2
2 

 2
 1,5t  3,62t  2 t   
 14t 2 3,62t  t   
 36
3    12
 2,62 t


Figura 4
1,287 t
 Figura 3’ i 3”


Jy s



 175,67t 4  29,43t 4  2  2,57t 4  100,77t 4  311,00t 4 ,

2
3
 2t  3t 3   6t  t 3 


t

3
t
1



 Jy  
 1,5t 2  0,5t   3t   

  2
36
3

 
 12   12 


1,5 t

Figura 3’ i 3”
Figura 1
Figura 2


 2 t  ( 7 t )3 
4
4
4
4
4

  4,5t  0,5t  2  4,125t  57,17t  70,42t .
 12 
Figura 4
09 Momenty bezwładności figur płaskich.doc
111