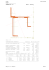Przykład 4.1.´Sci ˛ag stalowy I120 L200x100x10 P 10 cm 10 cm

Przykład 4.1.´Sci ˛ag stalowy I120 L200x100x10 P 10 cm 10 cm

Przykład 4.1. Ściag
˛ stalowy
10 cm
Obliczyć dopuszczalna˛ sił˛e P rozciagaj
˛ ac
˛ a˛ ściag
˛ stalowy o przekroju pokazanym na poniższym
rysunku jeśli napr˛eżenie dopuszczalne wynosi 215 MPa. Szukana siła P przyłożona jest w środku ci˛eżkości dwuteownika.
P
10 cm
L200x100x10
I120
Rozwiazanie
˛
Rozpatrywany przekrój ściagu
˛ jest przekrojem złożonym z dwóch kształtowników: dwuteownika I120 i katownika
˛
nierównoramiennego L200x100x10. Wartości charakterystyk geometrycznych użytych kształtowników zaczerpni˛eto z „Tablic do projektowania konstrukcji stalowych”, W. Bogucki i M. Żyburtowicz, wyd. 6, Warszawa, 1995r. Poniżej, i na stronie nast˛epnej,
zamieszczono potrzebne do rozwiazania
˛
rozpatrywanego zadania wielkości charakterystyczne
w takim układzie współrz˛ednych, jaki przyj˛ety jest w „Tablicach”.
- dwuteownik I120:
Y
h = 120 mm
bf = 58 mm
A = 14,2 cm2
Ix = 328 cm4
Iy = 21,5 cm4
h
X
bf
1
- katownik
˛
nierównoramienny L200x100x10:
η
Y
α
b
ξ
ey
X
b = 200 mm
a = 100 mm
ex = 2,01 cm
ey = 6,93 cm
tg α = 0,263
A = 29,2 cm2
Ix = 1219 cm4
Iy = 210 cm4
Iη = 135,2 cm4 = Imin
ex
a
W celu obliczenia maksymalnej dopuszczalnej wartości siły P należy obliczyć ekstremalne
napr˛eżenia w ściagu,
˛ traktujac
˛ wartość siły P jako znana,˛ a nast˛epnie tak obliczone napr˛eżenie
porównać z wartościa˛ dopuszczalna.˛
W poniższym przykładzie zaprezentowane sa˛ dwa sposoby obliczenia napr˛eże ń normalnych.
W pierwszym napr˛eżenia określa si˛e korzystajac
˛ ze wzoru na napr˛eżenia normalne wzgl˛edem
osi głównych centralnych, w drugim z bardziej ogólnego wzoru na napr˛eżenia normalne wzgl˛edem osi centralnych.
Niezależnie od przyj˛etego sposobu rozwiazanie
˛
zadania rozpoczać
˛ należy od określenia charakterystyk geometrycznych rozpatrywanego przekroju złożonego.
2
1. Wyznaczenie środka ci˛eżkości
W celu wyznaczenia środka ci˛eżkości przyj˛eto wst˛epny układ
˛ współrz˛ednych Y1 OZ1 .
10 cm
2,01 cm
O = CI
Z1
6,93 cm
10 cm
CL
Y1
12 cm
10 cm
W tym układzie obliczone sa˛ momenty statyczne Sy1 i Sz1 :
1
· 12 + 2,01 = 0 + 29,2 · 8,01 = 233,9 cm3
Sy1 = 14,2 · 0 + 29,2 ·
2
Sz1 = 14,2 · 0 + 29,2 · (10 − 6,93) = 0 + 29,2 · 3,07 = 89,64 cm3
Pole przekroju A ma zaś wartość
A = 14,2 + 29,2 = 43,4 cm2
Tak wi˛ec, środek ci˛eżkości C ma nast˛epujace
˛ współrz˛edne w układzie Y1 OZ1 :
Sz 1
89,64
=
= 2,066 cm
A
43,4
Sy
233,9
zc = 1 =
= 5,389 cm
A
43,4
yc =
3
2. Wyznaczenie centralnych momentów bezładności
Przyjmijmy nowy centralny układ współrz˛ednych Yc CZc .
2,01 cm
O = CI
C
10 cm
CL
Y1
Yc
12 cm
Z1
Zc
6,93 cm
2,066 cm
10 cm
5,389 cm
10 cm
Dla tak przyj˛etego układu współrz˛ednych obliczane sa,˛ przy pomocy wzorów Steiner’a, centralne momenty bezwładności:
Iyc = 328 + 14,2 · (−5,389)2 + 210 + 29,2 · (−5,389 + 8,01)2 =
= 328 + 412,4 + 210 + 29,2 · 2,6212 = 1151 cm4
Izc = 21,5 + 14,2 · (−2,066)2 + 12194 + 29,2 · (−2,066 + 3,07)2 =
= 21,5 + 60,58 + 1219 + 29,2 · 1,0042 = 1331 cm4
Aby obliczyć dewiacyjny moment bezwładności Iyc zc rozpatrywanego przekroju potrzebna jest
znajomość dewiacyjnego momentu bezwładności katownika
˛
nierównoramiennego wchodza˛
cego w skład przekroju złożonego (dla dwuteownika jest on oczywiście równy zeru, gdyż dwuteownik jest figura˛ symetryczna).
˛ Nieznany moment katownika
˛
można łatwo obliczy ć wykorzystujac
˛ inne wielkości charakterystyczne katownika.
˛
W tym celu wystarczy przekształcić
znany wzór na wartośc kata
˛ nachylenia osi głównych:
tg 2α =
−2Ixy
Ix − I y
=⇒
1
Ixy = − (Ix − Iy ) · tg 2α
2
Wartości Ix i Iy sa˛ dane, zaś kat
˛ α obliczamy nast˛epujaco:
˛
tg α = 0,263
=⇒
α = 14, 74o
Stad
˛ wartość biegunowego momentu bezwładności katownika
˛
nierównoramiennego wchodza˛
cego w skład przekroju złożonego jest równa:
1
Ixy = − (1219 − 210) · tg(2 · 14,74o ) = −285,1 cm4
2
4
Inna metoda obliczenia nieznanej wartości Ixy polega na wykorzystaniu zależności pomi˛edzy
warościami momentów bezwładności:
- wzoru na promień koła Mohra
Jx − J y
2
2
+
Jxy2
=
J1 − J 2
2
2
=⇒
Jxy2
=
J1 − J 2
2
2
−
Jx − J y
2
2
- niezmiennika sumy momentów bezwładności
Jx + Jy = J1 + J2 =⇒ J1 = Jx + Jy − J2
Po podstawieniu odpowiednich wartości otrzymujemy:
J1 = 1219 + 210 − 135,2 = 1293,8 cm4
2 2
2
1293,8 − 135,2
1219 − 210
2
Jxy =
−
= −284,7 cm4
2
2
Jak widać wyniki otrzymane dwoma metodami różnia˛ si˛e. Jest to spowodowane zaokragleniami
˛
wartości tg α oraz Jmin charakteryzujacych
˛
przekrój katownika
˛
L200x100x10, które zostały
wykorzystane do obliczenia Jxy . Zakładajac,
˛ że obie te wielkości charakterystyczne obarczone
sa˛ identycznym bł˛edem zasadne jest przyj˛ecie do dalszych oblicze ń średnia˛ arytmetyczna˛ tych
dwóch wartości.
Jxy =
−285,1 − 284,7
= −284,9 cm4
2
Tak wi˛ec, można już obliczyć wartość momentu dewiacyjnego Iyc zc rozpatrywanego przekroju
złożonego:
Iyc zc = 0 + 14,2 · (−5,389) · (−2,066) + 284,9 + 29,2 · 1,004 · 2,621 = 519,8 cm 4
Dalszy algorytm post˛epowania uzależniony jest od przyj˛etego sposobu rozwiazywania.
˛
W przypadku obliczania napr˛eżeń normalnych wzgl˛edem osi głównych centralnych należy w pierwszej
kolejności wyznaczyć te osie.
SPOSÓB A - obliczenia przy użyciu wzorów określonych dla osi głównych centralnych
3.A. Wyznaczenie głównych centralnych osi i momentów bezładności
Kat
˛ nachylenia osi głównych Y i Z obliczamy nast˛epujaco:
˛
−2 · 519,8
−2Iyc zc
=
= 5,790
Iyc − I zc
1151 − 1331
=⇒ α = 40,10o
tg 2α =
5
=⇒
2α = 80,20o
=⇒
2,01 cm
10 cm
Z
O = CI
Zc
10 cm
CL
Y
Yc
12 cm
6,93 cm
C
10 cm
Zaś w celu obliczenia momentów głównych centralnych korzystamy z poniższego wzoru:
q
1
1
(Iyc − Izc )2 + 4Iyc z2c
I1,2 = (Iyc + Izc ) ±
2
2
W rozpatrywanym przypadku
I1,2
1
1
= (13314 + 1151) ±
2
2
= (1241 ± 527,5) cm4
q
(1331 − 1151)2 + 4 (−519,8)2 =
Tak wi˛ec, maksymalny główny centralny moment bezwładności I1 odpowiadajacy
˛ momentowi
Iz (gdyż Izc > Iyc ) oraz moment minimalny I2 = Iy maja˛ wartości:
I1 = 1241 + 527,5 = 1768 cm4
I2 = 1241 − 527,5 = 713,2 cm4
= Iz
= Iy
Sprawdzenie poprawności obliczeń można wykonać na dwa sposoby:
Iyc + I zc = I 1 + I 2
1331 cm + 1151 cm4 = 1768 cm4 + 713,2 cm4
2482 cm4 = 2482 cm4
4
Iyc Izc − (Iyc zc )2 = I1 I2
1331 cm4 · 1151 cm4 − (−519,8 cm4 )2 = 1768 cm4 · 713,2 cm4
1261194 cm8 = 1261194 cm8
Równoznaczność otrzymanych wyników z lewej i prawej strony potwierdza poprawność obliczeń.
6
4.A. Obliczenie mimośrodów siły
Aby wyznaczyć współrz˛edne punktu przyłożenia siły we współrz˛ednych Y CZ, które sa˛ jednocześnie mimośrodami przyłożenia siły, konieczne jest wyprowadzenie wzoru transformujacego
˛
znane współrz˛edne Yc CZc na współrz˛edne szukane. W rozpatrywanym przypadku wzór
ten ma postać:
y = yc cos α + zc sin α = yc cos 40,10o + zc sin 40,10o = 0,7649yc + 0,6441zc
(?)
z = −yc sin α + zc cos α = −yc sin 40,10o + zc cos 40,10o = −0,6441yc + 0,7649zc
Współrz˛edne punktu P przyłożenia obciażenia
˛
w układzie Y c CZc maja˛ wartość:
ycP = −2,066 cm
zcP = −5,389 cm
co oznacza, że mimośrody siły sa˛ równe:
y P = 0,7649 · (−2,066) + 0,6441 · (−5,389) = −5,051 cm
= ey
z P = −0,6441 · (−2,066) + 0,7649 · (−5,389) = −2,792 cm
= ez
5.A. Obliczenie sił przekrojowych
Zakłada si˛e, że składowe
˛
momentu zginajacego
˛
maja˛ znak dodatni, jeśli wektory, które je
reprezentuja˛ maja˛ kieruneki zgodne z kierunkami osi. Siła normalna jest zaś dodatnia wtedy,
gdy powoduje rozciaganie
˛
przekroju. Przy takich założeniach w dowolnym przekroju ściagu
˛
wyst˛epuja˛ nast˛epujace
˛ siły wewn˛etrzne:
N =P
My = N · ez = −2,792 · P
Mz = −N · ey = 5,051 · P
6.A. Wyznaczenie wzoru na napr˛ezenia normalne
Ponieważ mimośrodowe rozciaganie
˛
można traktować jako złożenie dwóch przypadków zginania prostego i rozciagania
˛
osiowego, napr˛eżenia normalne można zapisa ć w nast˛epujacej
˛
postaci:
σx = σxN + σxMz + σxMy =
Mz
My
N
±
y±
z
A
Iz
Iy
Znak przed składnikami napr˛eżenia zależnymi od momentów zginajacych
˛
ustala si˛e przeprowadzajac
˛ nast˛epujac
˛ a˛ analiz˛e:
Załóżmy, że moment Mz jest dodatni. Reguła śruby prawoskr˛etnej mówi, że taki
moment powoduje ściskanie włókien o dodatniej współrz˛ednej y. Oznacza to, że
dla Mz > 0 i y > 0 napr˛eżenie σxMz jest ujemne. Ponieważ moment bezwładności
Iz jest zawsze wi˛ekszy od zera napr˛eżenie normalne zależne od momentu M z musi
być wi˛ec opisane wzorem:
σxMz = −
Mz
y
Iz
7
Analogicznie określamy znak we wzorze na napr˛eżenie normalne zależne od momentu M y :
Załóżmy, że moment My jest dodatni. Reguła śruby prawoskr˛etnej mówi, że taki
moment powoduje rozciaganie
˛
włókien o dodatniej współrz˛ednej z. Oznacza to, że
M
dla My > 0 i z > 0 napr˛eżenie σx y jest dodatnie. Ponieważ moment bezwładności
Iy jest zawsze wi˛ekszy od zera napr˛eżenie normalne zależne od momentu M z musi
być opisane wzorem:
σxMy = +
My
z
Iy
Stad
˛ ostatecznie:
σx = σxN + σxMz + σxMy =
Mz
My
N
−
y+
z
A
Iz
Iy
7.A. Wyznaczenie osi oboj˛etnej
Oś oboj˛etna˛ wyznaczamy wiedzac,
˛ że napr˛eżenia na niej panujace
˛ sa˛ równe zero, stad:
˛
σx = 0
=⇒
=⇒
=⇒
Mz
My
N
−
y+
z = 0 =⇒
A
Iz
Iy
P
5,051P
−2,792P
−
y+
z = 0 =⇒
43,4
1768
713,2
2,304 · 10−2 P − 2,857 · 10−3 P y − 3,914 · 10−3 P z = 0
Aby obliczyć współrz˛edne przeci˛ecia osi głównych centralnych Y i Z przez szukana˛ oś oboj˛etna˛ należy przekształcić powyższe równanie prostej na postać odcinkowa.˛
y
z
+
=1
ay az
Przy czym
2,304 · 10−2
= 8,066 cm
−2,857 · 10−3
2,304 · 10−2
= 5,886 cm
az = −
−3,914 · 10−3
ay = −
Tak wi˛ec równanie osi oboj˛etnej ma postać:
σx = 0
=⇒
z
y
+
=1
8,066 5,886
Z powyższych przekształceń wynika, że oś oboj˛etna przechodzi przez punkty (5,886 cm;0)
i (0;8,066 cm).
8
Z
1
C
2
Y
8.A. Wyznaczenie napr˛eżeń w punktach przekroju najbardziej oddalonych od osi oboj˛etnej
Najbardziej oddalone od osi oboj˛etnej punkty przekroju oznaczono jako 1 i 2. Współrz˛edne
tych punktów w układzie Yc CZc wynosza˛ odpowiednio:
1
· 5,8 = 0,834 cm
2
1
zc1 = −5,389 − · 12 = −11,389 cm
2
yc1 = −2,066 +
yc2 = −2,066 + 10 = 7,934 cm
1
zc2 = −5,389 + · 12 + 10 = −11,611 cm
2
zaś ich współrz˛edne w układzie Y CZ obliczam wykorzystujac
˛ wzór (?) wyprowadzony w podrozdziale 4.A.:
y 1 = 0,7649 · 0,834 + 0,6441 · (−11,389) = −6,698 cm
z 1 = −0,6441 · 0,834 + 0,7649 · (−11,389) = −9,904 cm
y 2 = 0,7649 · 7,934 + 0,6441 · (−11,611) = −9,249 cm
z 2 = −0,6441 · 7,934 + 0,7649 · (−11,611) = 3,006 cm
9
Podstawiajac
˛ otrzymane współrz˛edne do wzoru na napr˛eżenia, otrzymujemy maksymalne i minimalne wartości napr˛eżeń w przekroju złożonym.
σx1 = σx (−6,698 cm; −9,904 cm) =
= 2,304 · 10−2 P − 2,857 · 10−3 P · (−6,698) − 3,914 · 10−3 P · (−9,904) =
= 7,838 · 10−2 P = σmax
σx2 = σx (−9,249 cm; 3,006 cm) =
= 2,304 · 10−2 P − 2,857 · 10−3 P · (−9,249) − 3,914 · 10−3 P · 3,006 =
= −2,558 · 10−2 P = σmin
W ten sposób obliczone zostały interesujace
˛ nas ekstremalne wartości napr˛eżeń normalnych.
oś oboj˛etna
7,838
σ [10 -2 P/cm 2 ]
-2,558
9.A. Obliczenie dopuszczalnej siły P
Dopuszczalna˛ wartość siły P obliczymy porównujac
˛ najwi˛eksze, niezależnie od znaku, napr˛eżenie w przekroju z napr˛eżeniem dopuszczalnym. Ponieważ oblicze ń dokonywaliśmy w centymetrach musimy przekształcić wartość σdop .
σdop = 215 MPa = 215 · 103
kN
kN
kN
= 215 · 103 4 2 = 21,5 2
2
m
10 cm
cm
10
max σx1 ; |σx2 | = σx1 = 7,838 · 10−2 P
=⇒
≤
P ≤
σdop = 21,5
kN
=⇒
cm2
21,5
= 274,3 kN
7,838 · 10−2
Tak wi˛ec ostatecznie
Pdop = 274,3 kN
Te same wyniki otrzymać można stosujac
˛ obliczenia wzgl˛edem osi centralnych, tj. w rozpatrywanym przypadku osi Yc i Zc .
SPOSÓB B - obliczenia przy użyciu wzorów określonych dla osi centralnych
3.B. Obliczenie mimośrodów siły
Współrz˛edne punktu P przyłożenia obciażenia
˛
w układzie Y c CZc maja˛ wartość:
ycP = −2,066 cm
zcP = −5,389 cm
4.B. Obliczenie sił przekrojowych
Niezmieniajac
˛ opisanych w punkcie 5.A. założeń dotyczacych
˛
znaków sił wewn˛etrznych można
zapisać wartości sił przekrojowych:
N =P
Myc = −5,389 · P
Mzc = 2,066 · P
5.B. Wyznaczenie wzoru na napr˛eżenia normalne
Wzór na napr˛eżenia normalne w rozpatrywanym układzie współrz˛ednych ma posta ć:
σx =
N
Jy z M y + J y c M z c
Jy z M z + J z c M y c
+ cc 2 c
y− c c 2 c
z
A
Jy c z c − J y c Jz c
Jy c z c − J y c Jz c
11
Podstawiajac
˛ znane wartości sił i momentów bezwładności otrzymujemy:
519,8 · (−P · 5,389) + 1151 · P · 2,066
P
+
y+
43,4
519,82 − 1151 · 1331
519,8 · P · 2,066 + 1331 · (−P · 5,389)
−
z=
519,82 − 1151 · 1331
−424,2 · P
−6097
P
+
y −
z=
=
43,4
−1261194
−1261194
= 2,304 · 10−2 P + 3,363 · 10−4 P y − 4,834 · 10−3 P z
σx =
6.B. Wyznaczenie osi oboj˛etnej
W celu wyznaczenia równania osi oboj˛etnej należy przyrównać wzór na napr˛eżenia normalne
do zera. Niezerowe współrz˛edne punktów przeci˛ecia osi współrz˛ednych z osia˛ oboj˛etna˛ maja˛
wartości:
2,304 · 10−2
= −68,51 cm
3,363 · 10−4
2,304 · 10−2
= 4,766 cm
a zc = −
−4,834 · 10−3
a yc = −
oś oboj˛etna
1
C
Yc
Zc
2
12
7.B. Wyznaczenie napr˛eżeń w punktach przekroju najbardziej oddalonych od osi oboj˛etnej
Z zamieszczonego na poprzedniej stronie rysunku widać, że najbardziej oddalonymi od osi
oboj˛etnej punktami sa˛ punkty 1 i 2, których współrz˛edne wynosza:
˛
y1 = −2,066 cm + 2,9 cm = 0,8345 cm
z1 = −5,389 cm − 6 cm = −11,389 cm
y2 = −2,066 cm + 10 cm = 7,934 cm
z2 = −5,389 cm + 6 cm + 10 cm = 10,61 cm
Podstawiajac
˛ obliczone współrz˛edne do wzoru na napr˛eżenia otrzymujemy napr˛eżenia ekstremalne.
σx1 = σx (0,8345 cm; −11,389 cm) =
= 2,304 · 10−2 P + 3,363 · 10−4 P · 0,8345 − 4,834 · 10−3 P · (−11,389) =
= 7,838 · 10−2 P = σmax
σx2 = σx (7,934 cm; 10,61 cm) =
= 2,304 · 10−2 P + 3,363 · 10−4 P · 7,934 − 4,834 · 10−3 P · 10,61 =
= −2,558 · 10−2 P = σmin
oś oboj˛etna
7,838
σ [10 -2 P/cm 2 ]
13
-2,558
8.B. Obliczenie dopuszczalnej siły P
Sprawdzenie warunku nośności przekroju ze wzgl˛edu na napr˛eżenia normalne prowadzi do
obliczenia dopuszczalnej wartości siły P .
max (σmax ; |σmin |) 6 σdop
=⇒
=⇒
=⇒
1
P 6
cm2
P 6 274,3 kN
=⇒
7,838 · 10−2
215 MPa = 215 ·
103 kN
kN
= 21,5 2
4
2
10 cm
cm
=⇒
Pdop = 274,3 kN
Jak łatwo zauważyć zastosowanie ogólniejszego wzoru (obowiazuj
˛ acego
˛
w układzie współrz˛ednych nie b˛edacych
˛
głównymi) nie wymaga wyznaczania współrz˛ednych punktu w obróconym
układzie współrz˛ednych oraz obliczania charakterystyk przekroju w osiach głównych. Tak wi˛ec
zastosowanie sposobu B w rozpatrywanym przypadku jest bardziej racjonalne ze wzgl˛edu na
nakład obliczeń.
14