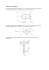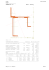pomoc dydaktyczna

GEOMETRIA MAS – momenty bezwładności i dewiacji
Zasady ogólne:
1) Moment bezwładności względem osi równy jest sumie momentów bezwładności względem dwóch
prostopadłych płaszczyzn zawierających tę oś:
I x =I π xy+ I π xz
I y =I π xy+ I π yz
I z= I π xz +I π yz
2) Moment bezwładności względem punktu równy jest sumie momentów bezwładności względem trzech
prostopadłych płaszczyzn przecinających się w tym punkcie:
I o=I π xy + I π xz + I π yz
lub równy jest połowie sumy momentów bezwładności względem trzech prostopadłych osi przechodzących
przez ten punkt:
1
I o= (I x + I y + I z)
2
3) Dla ciał jednorodnych czyli o stałym rozkładzie gęstości (lub układu ciał o jednakowej gęstości) masowy
moment bezwładności to iloczyn gęstości ciała i geometrycznego momentu bezwładności:
I = ρ IG
Aby przejść z masowego momentu na geometryczny należy moment masowy podzielić przez gęstość ciała
lub zastąpić masę objętością (bryła – 3D), polem powierzchni (cienka płytka lub figura – 2D), długością (cienki
pręt-1D) (gęstość odpowiednio objętościowa, powierzchniowa, liniowa).
4) W mechanice wykorzystuje się masowe momenty bezwładności, jednostka [kg m^2],
w wytrzymałości materiałów (dla przekrojów ciał – 2D) stosuje się geometryczne momenty bezwładności,
jednostka [m^4].
5) Momenty bezwładności są zawsze dodatnie, momenty dewiacji mogą być dodanie, ujemne lub równe zero.
6) Twierdzenie Steinera dla momentów bezwładności
Moment bezwładności ciała względem danej osi równy jest sumie momentu bezwładności ciała względem
osi do niej równoległej i przechodzącej przez środek masy ciała (centralnej) oraz iloczynu masy ciała przez
kwadrat odległości między osiami, np. dla osi x:
I x = I x + me 2
C
Twierdzenie to obowiązuje również dla płaszczyzny i punktu.
7) Twierdzenie Steinera dla momentów dewiacji
Moment dewiacji ciała względem dwu prostopadłych płaszczyzn równy jest sumie momentu dewiacji
względem dwu płaszczyzn równoległych do danych płaszczyzn i zawierających środek masy (centralnych)
ciała oraz iloczynu masy ciała przez współrzędne określające położenie obu płaszczyzn względem płaszczyzn
centralnych, np.:
I xy = I π xz π yz = I x y + mek
C
C
W przypadku figur płaskich twierdzenie to dotyczy momentów dewiacji względem osi.
Anna Perek „Mechanika ogólna – pomoc dydaktyczna”, marzec 2014
str. 1
MOMENTY BEZWŁADNOŚCI – podstawowe wzory dla ciał jednorodnych
GRANIASTOSŁUP
WALEC
1
2
2
m(a + c )
12
1
2
2
I y = m(b + c )
12
1
I z = m(a 2 +b 2)
12
1 2 1
2
I x = I y = mr + mh
4
12
1
2
I z = mr
2
I x=
z
C
c
y
x
x’
y’
b
a
x’’
1
mc2
12
1
I π xz = ma 2
12
1
I π yz = mb2
12
z
z”
I π xy =
C
h
y
x
r
C
m = ρV =ρ π r 2 h
x’
I x' = ?
I y' = ?
I z' ' = ?
Rozwiązanie dokładne :
1
1
I x = I y = mr 2 + mh2
4
12
1 2
I z = mr
2
z
h
y
b
z
ale h≃0, stąd
(rozwiązanie przybliżone):
C
ale h≃0, stąd
(rozwiązanie przybliżone) :
a
x
y
r
1
I x =I y = mr 2
4
1
2
I z =I C = mr
2
x
1
2
ma
12
1
2
I y = mb
12
1
I z = m(a 2 +b 2)
12
I x=
(oś z skierowana jest prostopadle do
płytki - do nas)
1
I π xz =I π yz = mr 2
4
CIENKA PŁYTKA KOŁOWA
Rozwiązanie dokładne :
1
2
2
I x = m( a + h )
12
1
2
2
I y = m(b + h )
12
1
2
2
I z = m( a + b )
12
h
1
mh2
12
y’
I x' = ?
I y' = ?
I x'' = ?
CIENKA PŁYTKA PROSTOKĄTNA
I π xy =
2
m = ρV =ρ π r h
2
lub m = ρa A =ρa π r
gdzie ρa=ρ h
3
2
ρ [ kg / m ] ; ρa [ kg / m ]
PROSTOKĄT [przekrój
(figura) --> momenty geometryczne]
y’
1
1
IG=
Aa2 =
ba 3
12
12
x
1
1
2
3
IG=
Ab =
ab
12
12
y
C
y
b
a
x’
x
KOŁO [przekrój
(figura) --> momenty geometryczne]
y’
y
1 2
I G =I G = Ar
x
y 4
1
I G = Ar 2
C 2
C
gdzie : A=ab
r
I x' = ?
I y' = ?
Anna Perek „Mechanika ogólna – pomoc dydaktyczna”, marzec 2014
x
gdzie : A=π r 2
I y' = ?
str. 2
GRANIASTOSŁUP PROSTY (dowolna figura w
podstawie)
CIENKI PRĘT
Rozwiązanie dokładne :
1
1
I x = I y = mr 2 + mh2
4
12
z
1
I z = mr 2
2
z
h
I π xy=
1
mh2
12
ale r ≃0, stąd
(rozwiązanie przybliżone) :
C
C
y
c
gdzie :
m = ρV =ρ Ah
x
h
I x= I y=
x
1
2
mh
12
I z =0
A− pole powierzchni
podstawy
b
y
2r
m = ρV =ρ π r 2 h
lub m = ρb h
a
gdzie ρb=ρ A=ρ π r
2
3
ρ [ kg / m ] ; ρb [ kg / m ]
STOŻEK PROSTY
z
TRÓJKĄT [przekrój
I x = I y=
I z=
h
C
3
1
2
2
mr + mh
20
10
1
1
I G = Ah 2= ah 3
12
x 6
h
3
2
mr
10
I π xy =
1
gdzie : A= ah
2
1
2
mh
10
I π xz =I π yz =
r
(figura) --> momenty geometryczne]
y
3
mr 2
20
gdzie :
a
x
y
1
1
2
3
I G = Aa = ba
12
x 6
1
1
I G = Ab 2= ab 3
12
y 6
a
1
2
m = ρV = ρ π r h
3
x
KULA
1
gdzie : A= ab
2
x
b
PÓŁKULA
2 2
I x = I y =I z = mr
5
1 2
I π xz =I π yz =I π xy = mr
5
2 2
I x = I y =I z = mr
5
z
1 2
I π xz =I π yz =I π xy= mr
5
3 2
I C = mr
5
z
3 2
I O = mr
5
y’
r
C
r
gdzie :
y
4 3
m = ρV =ρ π r
3
C
O
gdzie :
y
x
x
1 4 3
2 3
m = ρV =ρ ( π r )=ρ π r
2 3
3
UWAGA : wzory te same co dla kuli , ale
masa we wzorach o połowę mniejsza ,
zatem moment wyjdzie o połowę mniejszy
IC = ?
I y' = ?
Anna Perek „Mechanika ogólna – pomoc dydaktyczna”, marzec 2014
str. 3
MASA SKUPIONA
PÓŁKOLE [przekrój
(figura) --> momenty geometryczne]
1
I G =I G = Ar 2
x
y 4
rotu
o ś ob
1 2
I G = Ar
O 2
x
y
I x =mr 2
r
x’
r
C
O
UWAGA: masa skupiona−ciało
o masie nie do pominięcia ,
jednak o niewielkich
wymiarach do pominięcia
m
gdzie :
1
2
A= ( π r )
2
UWAGA: wzory te same co dla koła ,
ale pole powierzchni we wzorach
o połowę mniejsze , zatem moment
wyjdzie o połowę mniejszy
x
IC = ?
I x' = ?
PÓŁ WALCA
ĆWIERĆ WALCA
I x= I y=
1
1
mh2+ mr 2
12
4
z
z
1
2
mh
12
1
I π xz =I π yz = mr 2
4
I π xy=
h
O
x
1
2 1
2
I x = I y = mH + mr
3
4
1 2
I z = mr
2
1 2
I z = mr
2
C
gdzie :
r
y’
y
1
m = ρV =ρ( π r 2) h
2
UWAGA: wzory te same co dla
walca , ale masa we wzorach
o połowę mniejsza , zatem
moment wyjdzie o połowę
mniejszy
O
H=½ h
1
I π xy = mH 2
3
1
I π xz =I π yz = mr 2
4
C
gdzie :
x
r
y
1
1
m = ρV =ρ( π r 2)( h)
2
2
UWAGA: wzory te same co dla walca
względem układu osi w podstawie ,
ale masa we wzorach 4 razy mniejsza
zatem moment wyjdzie 4 razy mniejszy
I y' = ?
Anna Perek „Mechanika ogólna – pomoc dydaktyczna”, marzec 2014
str. 4
PRZYKŁADOWE ZADANIA
ZAD.1
Wyznaczyć momenty bezwładności względem osi x i y cienkiej jednorodnej płytki stalowej o gęstości ρ i grubości b, w kształcie i
wymiarach pokazanych na rysunku. Dane: ρ=7.8 [g/m^3], a=5[cm], b=0.5 [cm].
y
Płytkę dzielimy na 3 części o prostych kształtach i znanych momentach bezwładności: [1] prostokąt, [2]
trójkąt, [3] półkole.
Moment bezwładności płytki względem danej osi jest sumą momentów od każdej części względem tej
osi:
I x =I x − I x + I x
I y =I y − I y + I y
4a
1
2
3
1
2
3
[1] prostokąt
Z tw. Steinera:
2
I x =I x +m( 2a)
1
2
I x = m( 4a)
12
1
1
2
2
2
I x = m( 4a) + m(2a ) =5 ma
12
3
1
O
C1
x
a
m=ρa A
ρa=ρ b
A=( 2a)( 4a)=8a 2
C1
3
2
y
I y = I y + m(a )
1
2
I y = m( 2a )
12
1
1
2
2
2
I y = m(2a ) +m(a ) =1 ma
12
3
1
yC1
C1
a=0.05[m]
2
2
2
m=39[kg / m ]8(0.05) [m ]=0.78 [kg]
C1
1
3
ρ=7.8[ g /cm ]=7800[ kg/ m ]
b=0.5[cm ]=0.005[m]
3
2
ρa=7800[kg / m ]0.005 [m]=39[ kg/ m ]
1
1
1
I x =5 ⋅0.78 [ kg]⋅(0.05)2 [ m2 ]=0.0104[kgm2 ]
3
1
I y =1 ⋅0.78[ kg]⋅(0.05)2 [ m2 ]=0.0026[ kgm2 ]
3
1
C1
1
4a
xC1
2
I x =0.0104 [kgm ]
I y =0.0026[kgm2 ]
1
1
[2] trójkąt
O
x
2a
y
Wiemy, że dla płytki trójkątnej moment bezwładności względem osi (xT) wzdłuż krawędzi
wynosi:
1
a
I x = mh2
6
45
gdzie:
h=a
1
2
2
45
m=ρa A=ρa ( 2a) h=ρa ah=ρa a =39⋅(0.05) =0.0975[kg ]
2
1
I x = ⋅0.0975⋅(0.05)2=4.0625⋅10−5 [kgm2 ]
6
T
2
yC2
2a
1/3 h
xT
C2
h
xC2
o
o
T
−5
2
I x =4.0625⋅10 [ kgm ]
T
4a
Aby policzyć Ix2 trzeba dwukrotnie skorzystać z twierdzenia Steinera:
2
2
1
1
I x =I x + m( h) ⇒ I x = I x −m( h)
3
3
T
C2
C2
T
2
2
I x = I x + m( 4a + h)
3
2
C2
2
O
2
x
2
1
2
I x = I x −m( h) + m(4a + h)
3
3
T
2
1
2
1
7
2
2 196
2
2
I x = I x − ma + m (4a + a) =I x − ma +
ma = I x + 21 ma
9
3
9
9
9
2
T
T
Anna Perek „Mechanika ogólna – pomoc dydaktyczna”, marzec 2014
T
str. 5
7
−5
2
−3
2
I x =4.0625⋅10 +21 ⋅0.0975⋅(0.05) =5.349⋅10 [kgm ]
9
2
−3
2
I x =5.349⋅10 [kgm ]
2
yC2
y
A
C
a
D
a
Moment bezwładności trójkąta względem osi (y).
Z tw. Steinera:
I y =I y +ma 2
2
C2
Aby wyznaczyć moment względem osi yC2 podzielmy trójkąt na dwa ABC i BCD, każdy o
połowie masy całego. Wtedy oś yC2 będzie przechodziła przez krawędź każdego z nich.
1 1
2
I y ( jednego)= ( m)a
6 2
1 1
1
I y =2⋅ ( m)a 2= ma2
6 2
6
1
1
2
2
−5
2
I y = ma = ⋅0.0975⋅(0.05) =4.0625⋅10 [ kgm ]
6
6
B
C2
C2
C2
I y =4.0625⋅10−5+ 0.0975(0.05)2=2.8437⋅10−4 [ kgm2 ]
2
[3] półkole
y
yC3
Wiemy, ze dla płytki w kształcie półkola moment bezwładności względem średnicy (oś x)
wynosi:
1
2
O
3
a C
2
x
I x = ma
4
1
1
2
2
m = ρa A =ρa ( π a )=39⋅ ⋅(π⋅0.05 )=0.1531[kg ]
2
2
1
2
−5
2
I x = ⋅0.1531⋅0.05 =9.568⋅10 [kgm ]
4
I x =9.568⋅10−5 [ kgm2 ]
3
Moment bezwładności trójkąta względem osi (y).
Z tw. Steinera:
I y =I y +ma 2
3
C3
1
1
I y = ma 2= ⋅0.1531⋅0.052=9.5687⋅10−5 [kgm2 ]
4
4
−5
I y =9.5687⋅10 +0.1531⋅0.05 2=4.7844⋅10−4 [ kgm2 ]
C3
3
I y =4.7844⋅10−4 [kgm2 ]
3
Całkowite momenty bezwładności wynoszą:
I x = I x − I x + I x =0.0104−5.349⋅10−3 +9.568⋅10−5=5.1467⋅10−3 [kgm 2]
I y =I y − I y + I y =0.0026−2.8437⋅10−4+ 4.7844⋅10−4=2.7941⋅10−3 [kgm2 ]
1
2
3
1
2
3
ostatecznie:
I x =5.1467⋅10−3 [kgm2 ]
I y =2.7941⋅10−3 [ kgm2 ]
Anna Perek „Mechanika ogólna – pomoc dydaktyczna”, marzec 2014
str. 6