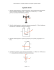W punkcie K przekroju α−α obliczyć naprężenia główne i określić

W punkcie K przekroju α−α obliczyć naprężenia główne i określić (obliczyć i narysować) kierunki
główne.
α
z
30 kNm
α
x
3m
3m
Przekrój poprzeczny (α−α i każdy inny), wymiary w [cm]:
4
24
K
5
2
20
2
Rozwiązanie:
Wyznaczenie sił przekrojowych w przekroju α−α.
α−α
Siły przekrojowe w przekroju α−α można obliczyć bezpośrednio, ale dla przypomnienia narysowano
wykresy M i Q (N≡0).
M
30
[kNm]
10
[kN]
30
Q
W przekroju α−α występuje moment zginający 30 kNm rozciągający włókna dolne i siła poprzeczna 10 kN, czyli naprężenia styczne τxz będą dodatnie (układ: x-prawo, z-góra)
Charakterystyki geometryczne przekroju:
Przekrój ma pionową oś symetrii, czyli jest na osią centralną główną – oznaczymy ją z .
Druga oś centralna główna jest prostopadła do z i przechodzi przez środek ciężkości, więc trzeba go
znaleźć.
Moment statyczny względem dolnej krawędzi przekroju Syo obliczymy dzieląc przekrój na trzy części:
górną półkę 4*24 cm i dwa „boki” 24*2 cm. Licząc dalsze charakterystyki wykorzystamy ten sam
podział.
z
4
9
y
24
zK= -14
zo=19
K
5
I
2
yo
20
2
Syo = 4*24*26 + 2 [24*2*12] = 24 (104+48) = 3648 cm3
Pole: F = 4*24 + 2 [24*2] = 24*8 = 192 cm2
Położenie środka ciężkości: zo = Syo/F = 19 cm (pokazano na rysunku powyżej)
Moment bezwładności względem osi centralnej głównej y.
Jy = 43*24/12 + 4*24*(9-2)2 + 2 [243*2/12 + 24*2*(19-12)2] = 14144 cm4
W obliczeniach powyżej zastosowano wzór Steinera.
Naprężenie normalne σx w punkcie K przekroju α−α.
α−α
Zastosujemy konwencję znakowania momentów zginających: momenty rozciągające „spody” (które
domyślnie przyjęto na dole) są dodatnie. W takim razie Mα = 30 kNm (plus)
Jeżeli stosujemy tą konwencję, to trzeba zastosować wzór:
− Mα
(rozkład σx w przekroju α−α)
σ x (α) =
z
Jy
Naprężenie σx w p. K wyniesie:
σ x(K) =
− Mα
zK
Jy
gdzie współrzędna z punktu K w układzie (y-z) wynosi zK = - 14 cm (patrz rysunek powyżej)
− 30 ⋅ 10 3 Nm
czyli:
σ x(K) =
− 14 ⋅ 10 2 m = 29,695 MPa
−8
4
14144 ⋅ 10 m
Naprężenie styczne τxz w punkcie K przekroju α−α.
Przekrój poprzeczny podzielono na wysokości punktu K na dwie części. Obliczono wartość
bezwzględną momentu statycznego części zakreskowanej:
|SyI| = 5*2*(14+2,5) = 165 cm3
Szerokość przecięcia: b = 2 cm
− Q α ⋅ S Iy
10 ⋅ 10 3 N ⋅ 165 ⋅ 10 −6 m 3
τ xz ( K ) =
=
= 0,5833 MPa
Jy ⋅b
14144 ⋅ 10 −8 m 4 ⋅ 2 ⋅ 10 − 2 m
Uwaga: Gdyby przecięto przekrój poziomą linią na wysokości zK to na dole byłyby dwie części o
momencie statycznym dwa razy większym niż jedna (zakreskowana) część, ale szerokość przecięcia też
wzrosłaby dwukrotne. Wynik liczbowy po zastosowaniu wzoru na τxz byłby identyczny jak powyżej, ale
należy unikać podziału przekroju na trzy lub więcej części. Proszę pamiętać że wyprowadzając wzór
rozpatrywano równowagę przy podziale przekroju poprzecznego na dwie części.
Stan naprężenia w punkcie K.
W układzie współrzędnych (x-z) stan naprężenia w punkcie K opisuje tensor:
 σ x ( K ) τ xz ( K )  29,695 0,5833
Tσ( K ) = 
MPa
=
0 
τ xz ( K ) σ z ( K )  0,5833
(
)
Nie zapisywano drugiego wiersza i drugiej kolumny tensora ponieważ występują tam wartości zerowe,
czyli w punkcie K istnieje płaski stan naprężeń.
Naprężenia główne obliczymy ze wzoru: σ1 / 2 =
czyli: σ1 = 29,706 MPa,
σx 1
±
σ 2x + 4 τ 2xz
2 2
(bo σz = 0)
σ2 = - 0,01145 MPa
− τ xz
τ
Kierunki główne naprężeń:
tg α i =
= xz
σz − σi
σi
czyli
tg α1 = 0,5833/29,706 = 0,019636
α1 = 1,125o
tg α2 = 0,5833/(-0,01145) = -50,943
α2 = -88,875o
Graficzne obrazy Tσ w punkcie K w płaszczyźnie pionowej prostopadłej do płaszczyzny przekroju:
0,01145
0,5833
29,706
29,695
0,5833
29,695
29,706
α1
0,5833
z
x
0,5833
0,01145
- w układzie osi (x-z)
- w układzie osi głównych Tσ
Na rysunku strzałki nie są w skali reprezentującej wartości naprężeń (niektóre musiałyby być
niezauważalnie małe), ale poprawnie reprezentują znaki naprężeń. Kąt α1 też jest powiększony na
rysunku w stosunku do rzeczywistości.