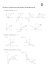Pochodna funkcji jednej zmiennej - Polsko

Analiza Matematyczna
Pochodna funkcji jednej zmiennej
Alexander Denisjuk
[email protected]
Polsko-Japońska Wyższa Szkoła Technik Komputerowych
zamiejscowy ośrodek dydaktyczny w Gdańsku
ul. Brzegi 55
80-045 Gdańsk
Analiza Matematyczna – p. 1
Pochodna funkcji jednej zmiennej
Najnowsza wersja tego dokumentu dostepna
˛
jest pod adresem
http://users.pjwstk.edu.pl/~denisjuk/
Analiza Matematyczna – p. 2
Pojecie
˛
pochodnej
Niech dana bedzie
˛
funkcja y = f (x), określona w otoczeniu
(a, b) punktu x.
Definicja 1. 1. Liczba ∆x, taka że x + ∆x ∈ (a, b) nazywa sie˛
przyrostem zmiennej niezależnej x.
2. Liczba ∆y =
w punkcie x.
f (x + ∆x) − f (x) nazywa sie˛ przyrostem funkcji f
Lemat 2. Funkcja y = f (x) jest ciagła
˛
w punkcie x wtedy i tylko wtedy, gdy
przyrost funkcji w tym punkcie, ∆y = o(1) przy ∆x → 0.
Definicja 3.
∆y
1. Iloraz ∆x nazywa sie˛ ilorazem różniczkowym
2. Granica (o ile istnieje) f ′ (x)
∆y
∆x→0 ∆x
= lim
f (x+∆x)
nazywa
∆x
∆x→0
= lim
sie˛ pochodna˛ funkcji f w punkcie x.
3. Alternatywne oznaczenia: f ′ (x)
=
df
dx ,
y ′ (t) = ẏ(t).
Analiza Matematyczna – p. 3
Przykłady
Przykład 4.
2.
1.
f (x) = const =⇒ f ′ (x) = 0.
f (x) = x =⇒ f ′ (x) = 1.
3. Funkcja f (x)
= |x| nie ma pochodnej w punkcie 0.
Analiza Matematyczna – p. 4
Sens geometryczny pochodnej funkcji w punkcie
f (x + ∆x) − f (x)
P
ϕ(∆x)
M
∆x
ϕ0
ϕ(∆x)
x
N
x + ∆x
Analiza Matematyczna – p. 5
Komentarze do rysunku
Definicja 5. Prosta, przechodzaca
˛ przez punkty M i P nazywa sie˛ sieczna˛
• Kat
˛ pochylenia stycznej M P jest funkcja˛ od ∆x, oznaczmy
jego przez ϕ(∆x).
• Z trójkata
˛ M P N widać, że tg ϕ(∆x) =
∆y
∆x .
• W taki sposób, przy ∆x → 0 (P → M ) istnieje położenie
graniczne stycznej wtedy i tylko wtedy, gdy istnieje f ′ (x).
Definicja 6. Prosta y = f (x0 ) + f ′ (x0 )(x − x0 ) jest styczna˛ do wykresu
funkcji y = f (x) w punkcie x0 .
f ′ (x) zgadza sie˛ z tangensem kata
˛ pochylenia stycznej.
Uwaga 8. Funkcja y = f (x), która ma pochodna˛ nazywa sie˛ również gładka.
˛
Uwaga 7.
Analiza Matematyczna – p. 6
Funkcje różniczkowalne
Definicja 9. Funkcja y = f (x) nazywa sie˛ różniczkowalna˛ w punkcie x,
jeżeli ∃A ∈ R, takie że ∆y = A · ∆x + o(∆x) przy ∆x → 0.
= f (x) jest różniczkowalna w punkcie x0 wtedy
i tylko wtedy, gdy istnieje f ′ (x0 ).
∆y
Dowód. ⇒: lim ∆x = lim A + o(1) = A.
Twierdzenie 10. Funkcja y
∆x→0
∆y−f ′ (x0 )·∆x
⇐: lim
∆x
∆x→0
∆x→0
= 0 =⇒ ∆y = f ′ (x0 )∆x + o(∆x).
Wniosek 11. Liczba A w definicji 9 równa jest f ′ (x0 ).
Twierdzenie 12. Funkcja różniczkowalna w punkcie jest ciagł
˛ a˛ w tym punkcie.
Analiza Matematyczna – p. 7
Różniczkowalnie funkcji złożónej
Twierdzenie 13. Niech funkcja x = ϕ(t) bedzie
˛
różniczkowalna˛
w punkcie t0 , zaś funkcja y = f (x) bedzie
˛
różniczkowalna˛
w punkcie x0 = ϕ(t0 ). Wtedy funkcja złożona f (ϕ(t)) bedzie
˛
różniczkowalna˛ w punkcie t0 , przy czym
Dowód.
′
′
′
f ϕ(t0 ) = f ϕ(t0 ) · ϕ (t0 )
• ∆x = φ′ (t0 )∆t + o(∆t).
′
• ∆y =
ϕ(t0 ) ϕ (t0 )∆t + o(∆t) +
0 )∆x + o(∆x) =
o(∆t) = f ′ ϕ(t0 ) ϕ′ (t0 )∆t + o(∆t).
f ′ (x
f′
Analiza Matematyczna – p. 8
Różniczkowalnie funkcji odwrotnej
Twierdzenie 14. Niech f (x) bedzie
˛
funkcja˛ rosnac
˛ a˛ (malejac
˛ a)
˛ i ciagl
˛ a˛
w otoczeniu punktu x0 , oraz różniczkowalna˛ w punkcie x0 i f ′ (x) 6= 0.
Wtedy w otoczeniu punktu y0 = f (x0 ) określona jest funkcja odwrotna
x = f −1 (y), która jest rosnac
˛ a˛ (malejac
˛ a)
˛ i ciagł
˛ a˛ w otoczeniu y0 oraz
różniczkowalna w punkcie y0 i
Dowód.
•
∆x
∆y
=
1
∆y
∆x
f
−1
′
(y0 ) =
1
.
f ′ (x0 )
.
• Za moca˛ ciagłości
˛
∆y → 0 ⇐⇒ ∆x → 0.
∆x
∆y→0 ∆y
• Wiec
˛ lim
=
1
lim
∆y
∆x
∆x→0
.
Analiza Matematyczna – p. 9
Sens geometryczny pochodnej funkcji odwrotnej
y
α
x
β
tg α =
1
tg β ,
gdy α + β =
π
2
Analiza Matematyczna – p. 10
Różniczkowanie sumy, różnicy, iloczynu i ilorazu funkcji
Twierdzenie 15. Niech funkcje u(x) oraz v(x) bed
˛ a˛ różniczkowalne
w punkcie x. Wtedy suma, różnica, iloczyn i iloraz (iloraz w przypadku
v(x) 6= 0) sa˛ różniczkowalne w punkcie x, przy czym
′
1. u(x) ± v(x) = u′ (x) ± v ′ (x),
′
2. u(x) · v(x) = u′ (x) · v(x) + u(x) · v ′ (x),
i′
h
u′ (x)·v(x)−u(x)·v ′ (x)
u(x)
.
3. v(x) =
v 2 (x)
Analiza Matematyczna – p. 11
Pochodne funkcji elementarnych
Twierdzenie 16.
1.
(loga x)′ =
2.
(lna
x)′
=
1
x
· loga e,
1
x,
(ax )′ = ax · ln a,
4. (ex )′ = ex ,
3.
(xa )′ = a · xa−1 ,
6. (sin x)′ = cos x,
7. (cos x)′ = − sin x,
5.
1
cos2 x ,
9. (ctg x)′ = − sin12 x ,
8.
(tg x)′ =
√ 1
,
1−x2
10.
(arcsin x)′ =
11.
1
(arccos x)′ = − √1−x
,
2
12.
(arctg x)′ =
13.
1
(arcctg x)′ = − 1+x
2,
14.
(sinh x)′ = cosh x,
15.
(cosh x)′ = sinh x,
1
1+x2 ,
1
,
cosh2 x
1
.
17. (ctgh x)′ = sinh
2
x
16.
(tgh x)′ =
Analiza Matematyczna – p. 12
Dwód twierdzenia 16
∆ loga x
loga (x+∆x)−loga (x)
1 x
=
=
x ∆x
i ∆x
h ∆x
x
1
∆x ∆x
1
−→
1
+
log
loga e.
a
x
x
x
∆x→0
Dowód.
3 (ax )′
1
=
1
(loga y)′
=
1
y
1
loga e
=
y
loga e
loga (1 +
∆x
x )
=
= ax · ln a.
= (ea ln x )′ = ea ln x · (a ln x)′ = xa · a x1 = axa−1 .
∆x
2 cos x+ 2 sin ∆x
sin(x+∆x)−sin x
∆ sin x
2
6 ∆x =
=
=
∆x
∆x
∆x
∆x sin 2
cos x + 2
−→ cos x.
∆x
∆x→0
2
′
π
′
7 (cos x) = sin( 2 − x) = cos( π2 − x) · ( π2 − x)′ = − sin x.
′
(sin x)′ cos x−sin x(cos x)′
sin x
cos2 x+sin2 x
1
′
=
8 (tg x) = cos x
=
=
2
2
cos x
cos x
cos2 x .
5 (xa )′
–verte–
Analiza Matematyczna – p. 13
Dwód twierdzenia 16, cd
Dowód. cd.
10 (arcsin x)′
=
1
(sin y)′
=
1
cos y
=
1
cos arcsin x
= (tg1y)′ = cos2 y = cos2 (arctg x) =
x −x ′
ex +e−x
=
= cosh x.
14 (sinh x)′ = e −e
2
2
12 (arctg x)′
=
√ 1
.
1−x2
1
1+x2 .
Analiza Matematyczna – p. 14