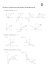Analiza Matematyczna 1 MAP 1091 Lista 1

Analiza Matematyczna 1
MAP 1091
Lista zdań obejmuje cały materiał kursu i jest podzielona na 15 jednostek odpowiadających zakresem kolejnym wykładom. Na ćwiczeniach należy rozwiązać przynajmniej jeden podpunkt z każdego
zadania. Wyjątkiem są zadania oznaczone literą (P) oraz symbolem (*). Zadania oznaczone literą (P)
są proste. Z reguły są to jednoetapowe zadania typu „wstaw do wzoru”. Te zadania należy rozwiązać
samodzielnie. Z kolei zadania oznaczone gwiazdką (*) są trudniejsze. Te nieobowiązkowe zadania kierujemy do ambitnych studentów.
Zachęcamy studentów do weryfikowania rozwiązań zadań za pomocą programów komputerowych.
W Internecie można znaleźć wiele programów do obliczeń numerycznych i symbolicznych. Programy
te można wykorzystać m.in. do rysowania wykresów funkcji, obliczania granic ciągów i funkcji, znajdowania pochodnych, wyznaczania całek nieoznaczonych i oznaczonych, rozwiązywania układów równań
algebraicznych i różniczkowych, badań statystycznych itp. Szczególnie polecamy stronę internetową
Wolfram Alpha. Można także korzystać z darmowych programów: Maxima, Microsoft Mathematics, Octave, R, Sage, Scilab, a także programów płatnych: Derive, Mathematica, Matlab,
Maple, Scientific WorkPlace. Wiele popularnych kalkulatorów naukowych jest zaprogramowanych
do wykonywania obliczeń numerycznych i symbolicznych oraz do prezentowania wykresów funkcji.
Uzdolnionych studentów zachęcamy do przygotowania się w czasie semestru i następnie udziału w
egzaminach na ocenę celującą z algebry i analizy. Zadania z tych egzaminów z ubiegłych lat można
znaleźć na stronie internetowej
http://www.im.pwr.wroc.pl/kursy-ogolnouczelniane/oceny-celujace.html
Przed kolokwiami i egzaminami warto zapoznać się z zestawieniem typowych błędów popełnianych
przez studentów na sprawdzianach z matematyki.
http://prac.im.pwr.wroc.pl/˜skoczylas/typowe bledy studentow.pdf
Opracowanie: dr Marian Gewert, doc. Zbigniew Skoczylas
Wrocław, wrzesień 2013
Lista 1
1. Określić i narysować dziedziny funkcji:
x
x−2
(a) f (x) = 2
; (b) f (x) = 2
;
x − 2x − 3
x +4
2*. Wyznaczyć zbiory wartości funkcji:
√
(a) f (x) = x2 + 2x;
(b) f (x) = − x + 2;
(d) f (x) = 1 +
1
;
x+1
(e) f (x) =
x2 − 1
;
x+1
(c) f (x) =
p
16 − x2 ;
x2
;
x2 + 1
x4 − 9
(f) f (x) = 2
.
x −3
(c) f (x) =
1
x−1
(d) f (x) = √
.
x−1
3. Na podanych przedziałach uzasadnić monotoniczność funkcji:
√
(a) f (x) = x2 , (−∞, 0] ;
(b) f (x) = x − 1, [1, ∞);
1
(c) f (x) =
, [0, ∞) ;
(d*) f (x) = x + |x|, R.
1 + x2
4 (P). Wyznaczyć współczynnik kierunkowy a oraz wyraz wolny b funkcji liniowych y = ax + b:
(a) y = 1;
(b) y − x = 0;
(c) y = −x + 4;
(d) y + 2x = 2;
(e) 3x + 4y − 2 = 0;
(f) x − 5y = 3.
5 (P). W podanych przedziałach uprościć wyrażenia:
(a) x + |2 − x| + 3|1 − x|, gdzie x ∈ (1, 2);
(b) |2x| − |x + 1| + 2|x − 2|, gdzie x ∈ (2, ∞);
|x − 1|
− |2 − 3x|, gdzie x ∈ (−∞, −1);
(d) ||1 − x| − 1| − 2|x − 2|, gdzie x ∈ (0, 1).
(c)
|x + 1|
6 (P). Funkcje kwadratowe sprowadzić do postaci iloczynowej (jeżeli istnieje) i naszkicować ich wykresy:
1
(a) f (x) = −x2 + x;
(b) f (x) = 2x2 + 1;
(c) f (x) = x2 + x + ;
4
3
9
(d) f (x) = x2 + 2x − 3;
(e) f (x) = −2x2 − 2x + ;
(f) f (x) = −x2 − 3x − .
2
4
7 (P). Wyznaczyć współczynniki oraz określić stopień funkcji wielomianowych:
(a) W (x) = (x + 1)3 − x(x − 1)2 ;
(b) W (x) = x4 + 4x3 − x2 (x + 2);
(c) W (x) = (x + 2)3 − (x − 2)2 ;
(d) W (x) = (x + 1)2 − (2x + 3)3 − 2x.
8. Naszkicować przykład wykresu funkcji wielomianowej, dla której podano jej pierwiastki, ich krotności oraz znak współczynnika przy najwyższej potędze zmiennej x:
(a) x1 = −2 (2–krotny), x2 = 0, x3 = 2, a4 > 0;
(b) x1 = −2, x2 = 1 (3–krotny), x3 = 2, a5 < 0;
(c) x1 = −2 (4–krotny), x2 = 0 (2–krotny), x3 = 2 (2–krotny), a8 > 0;
(d) x1 = −2 (3–krotny), x2 = 0 (3–krotny), x3 = 2 (2–krotny), a8 > 0.
9. Rozwiązać równania wymierne:
4x − 6
3
2
1
(a)
= 0;
(b)
+
= ;
2x2 − x + 4
4x − 6 2x − 3
5
(d)
2
21
3
+
= 2
;
x+1 x−2
x −x−2
(e)
2x − 1
3
=
+ 1;
x
x+1
10. Rozwiązać nierówności wymierne:
x2 − 3x
(x + 1)(x + 2)
(a)
< 0;
(b)
­ 0;
x+3
(x + 3)(x + 4)
(d)
x2 + 5x
> x;
x−3
(e)
(f)
(c) 2 +
x2 − 3x + 2
> 0;
x2 + 3x + 2
(f)
(c)
9x
3
=
+ 2;
3x − 1
3x + 1
x−4
2
x − 21
−
= 2
.
x−2 x+3
x +x−6
3
2
> ;
x+1
x
−x2 + 2x + 4
¬ 1.
x−2
Lista 2
11. Określić funkcje złożone f ◦ f , f ◦ g, g ◦ f , g ◦ g, jeżeli
1
(a) f (x) = x2 , g(x) = x + 1;
(b) f (x) = , g(x) = x2 ;
x
√
√
(d) f (x) = |x|, g(x) = x + 1.
(c) f (x) = x, g(x) = x4 ;
Wyznaczyć ich dziedziny.
2
12. Korzystając z wykresu funkcji f przedstawionego na rysunku
y
(A)
(B) y
y = f (x)
2
−2
2 x
naszkicować wykresy funkcji:
(a) f (x) + 1;
(b) f (−x) − 1;
(d) −f (x) + 1;
2
y=
2
,
x
(c) y = |x − 2|,
x
(f) f (1 − x) − 1.
13. Przekształcając wykresy funkcji y = x2 , y =
1
y = − x2 ,
2
1
y=
,
x+3
1
y = |x|,
3
4
(c) f (x + 1);
(e) −f (x − 1);
(a) y = x2 − 2,
y = f (x)
2
1
, y = |x| naszkicować funkcje:
x
y = (x + 3)2 ,
y=
y = x2 − 4x + 7;
3
;
x−1
y = 1 − |x|,
y = |x + 4| − 2.
14. Podany jest wykres funkcji y = f (x)
y
4
2
y = f (x)
3
x
1
Naszkicować wykresy funkcji:
(a) y = f (x + 1);
1
f (x);
2
(g) y = f (−x);
(d) y =
(b) y = f (x) − 2;
(c) y = f (x − 1) + 3;
(e) y = f (3x);
(f) y = −f (x);
(h) y = |f (x)|;
(i) y = f (|x|).
15 (P). Kąty wyrażone w stopniach zapisać w radianach, kąty wyrażone w radianach zapisać w stopniach:
(a) 10◦ ,
24◦ ,
45◦ ,
135◦ ,
350◦ ,
1080◦ ; (b) 1,
π
,
24
7π
,
12
4π
,
3
35
π,
36
21π
.
12
16 (P). Na płaszczyźnie narysować w położeniu standardowym kąty:
π
π
7π
7π
(a) ; (b) 120◦ ; (c) − ; (d) −270◦ ; (e)
; (f) − .
8
5
4
3
17. Korzystając
redukcyjnych zapisać podane wyrażenia w postaci funkcji trygonometrycz
ze wzorów
π
:
nych kąta α ∈ 0,
2
3π
5π
π
(a) sin
− α ; (b) cos
+ α ; (c) tg (π − α); (d) ctg
+α .
2
2
2
3
18. Zapisać w postaci funkcji trygonometrycznych kąta z pierwszej ćwiartki wyrażenia:
π
95
14
9
(a) sin − ; (b) cos π; (c) tg − π ; (d) ctg π.
3
2
3
9
Lista 3
19 (P). Obliczyć wartości wyrażeń:
19
5π
21
13π
(a) cos − π + cos ;
(b) cos − π − sin −
;
6
6
4
4
5
13
17
7
(d) ctg π + ctg − π .
(c) tg − π − ctg − π ;
3
3
6
6
20. Uzasadnić tożsamości trygonometryczne:
1
1 + tg α
= tg α;
(b) sin4 α+cos4 α = 1− sin2 2α;
(a)
1 + ctg α
2
α
1 − cos α
(d) tg =
;
(e) sin4 α−cos4 α = sin2 α−cos2 α;
2
sin α
Dla jakich kątów α są one prawdziwe?
21*. Wyprowadzić wzory:
α
2 tg
1 − tg2
2
(a) sin α =
α ; (b) cos α =
1 + tg2
1 + tg2
2
α
2
α;
2
(c) tg α + ctg α =
1
− cos α = sin α tg α.
cos α
(f)
α
2 ;
(c) tg α =
2 α
1 − tg
2
2 tg
2
;
sin 2α
α
1 − tg2
2
(d) ctg α =
α .
2 tg
2
22 (P). Korzystając z wykresu funkcji y = sin x naszkicować w przedziale [−π, π] wykresy funkcji:
x
(b) y = sin ;
3
(a) y = sin 2x;
π
(d) y = sin 2 x −
6
;
π
(c) y = sin x +
;
4
1
(f) y = sin x − 1.
2
(e) y = 1 + sin x;
23. Naszkicować wykresy funkcji:
1
π
;
(a) y = cos x − cos x ; (b) y = 1 + ctg x +
2
4
(c) y = tg x + | tg x|;
(d) y = |tg x| ctg x.
24. Rozwiązać równania trygonometryczne:
(a) sin x = − sin 2x;
π
π
(c) cos
− 2x = cos x +
;
4
3
π
π
−x ;
(e) tg x −
= tg
4
6
π
= ctg x;
(g) ctg 2x +
3
x
(b) cos 4x = sin ;
2
π
π
− 2x = cos x +
(d) sin
;
6
3
(f) ctg 2x = tg 2x;
π
(h) tg 2x +
4
π
= ctg 3x +
6
.
25. Rozwiązać równania trygonometryczne:
(a) sin2 x + cos x sin x = 0;
(d) tg x + tg 2x = tg 3x;
(b) sin x − 2 = cos 2x;
√
(e) sin x = 0;
26. Rozwiązać nierówności trygonometryczne:
√
π
x π
(a) 2 sin
− x ­ 3;
−
< −1;
(b) 2 cos
3
2
6
√
x π
π
(c) tg
+
> −1;
(d) 3 ctg 2x +
¬ 1.
4
3
4
4
(c) tg2 x − 2 tg x + 1 = 0;
1
(f) cos = 1.
x
27. Rozwiązać nierówności trygonometryczne:
r
x
π π
3
(a) cos x ¬ sin , x ∈ − ,
;
;
(b) cos x + sin x ­
2
2 2
2
π π
1
< 0;
(d) tg x tg 2x ¬ 1, x ∈ − ,
.
(c) ctg x −
ctg x
2 2
Lista 4
28. Rozwiązać równania wykładnicze:
2x−3
1
(a)
= 8;
(b) 2 · 42x − 3 · 4x = −1;
2
x
x+1
(d) 9 + 3
= 4;
(e) 5
8−3x
x
=5
2x
2−x
·5
x+5
3−x
(c)
;
(f)
√ x
5
3x
29. Rozwiązać nierówności wykładnicze:
4x−2
(a) 3
2−x
<9
;
(b) 0.25
3
(d) 2x − 2−x ¬ ;
2
(i)
x+1
x
(c) 2x
< 0.0625;
−
√
3
25 = 0;
1
+ 31−x = 0.
−4
2 −1
2
− 3x > 3x
2 −1
x2 + 2x −
1
(j) √ ¬ 2
2
1
1
< 2x
;
x
e −1
e +1
1
2
− 2x
√
<
2 +2
;
2.
30. Rozwiązać równania logarytmiczne:
(a) 4 log2 x = log2 81;
(b) log4 (x + 4) − log4 (x − 1) = 2;
(c) log 1 (x − 3) + log 1 x = −2;
2
2
(d) log2 x2 − 6 = 3 + log2 (x − 1).
31. Rozwiązać nierówności logarytmiczne:
(a) log5 (5 − 3x) > 1;
(b) log(3x − 1) − log(x − 1) > log 2;
1
2
­ 1 − log3 x; (d) ln x +
> 0.
(c)
log 1 x
ln x
3
32. Uzasadnić, że podane funkcje są różnowartościowe na wskazanych zbiorach:
1
(a) f (x) = 2x − 3, R;
(b) f (x) = , R \ {0};
(c) f (x) = x4 , [0, ∞).
x
33. Znaleźć funkcje odwrotne do funkcji:
√
x+1
;
(b) f (x) = 3 − 3 x + 2;
(a) f (x) =
x−1
(e) f (x) = log(x + 2); (f) f (x) = log 1 2x;
2
34 (P). Podaj wartości wyrażeń:
(a) arcsin
1
1
+ arccos ;
2
2
(b) arc ctg 1 · arc tg 1;
1
x
(c) f (x) = 2x−1 ;
(d) f (x) = 4 ;
(g) f (x) = log32 (x + 1).
√
3
arcsin
2 ;
(c)
arcsin 1
(d) arc tg
√
3 − arc ctg
√
3.
35. Określić dziedziny funkcji:
(a) f (x) = arcsin(2x + 1);
1
(c) f (x) = arc tg
;
x+1
1
(b) f (x) = arccos x +
;
2
(d) f (x) = arc ctg 2x .
36*. Obliczyć wartości wyrażeń:
1
1
; (b) ctg arcsin
;
(a) tg arccos
2
3
(c) sin arcsin
5
2
8
3
+ arcsin
;
5
17
(d) sin (arc tg 1 + arc tg 2).
37*. Funkcje odwrotne do podanych zapisać przy pomocy funkcji cyklometrycznych:
π 3π
(a) f (x) = sin x, x ∈
,
;
(b) f (x) = cos x, x ∈ [π, 2π];
2 2
3π π
;
(d) f (x) = ctg x, x ∈ (π, 2π).
(c) f (x) = tg x, x ∈ − , −
2
2
Lista 5
38. Korzystając z definicji granicy właściwej lub niewłaściwej uzasadnić równości:
3−n
1
(a) lim
= −1;
(b) lim 2 = 0;
(c) lim 2n = ∞.
n→∞ n + 4
n→∞ n
n→∞
39. Korzystając z twierdzeń o arytmetyce granic ciągów obliczyć granice:
3n − 1
;
n→∞ n + 4
3
n20 + 2
;
(d) lim
n→∞ (n3 + 1)20
n+1
;
n→∞ 2n2 + 1
1 + 3 + . . . + (2n − 1)
(e) lim
;
n→∞
2 + 4 + . . . + 2n
(a) lim
n3 + 2n2 + 1
;
n→∞
n − 3n3
5n − 4n
(f) lim n
;
n→∞ 5 − 3n
(b) lim
n2 + 1 n! + 1
(g) lim
;
n→∞ (2n + 1)(n + 1)!
(h) lim
n→∞
p
n2
+ 4n + 1 −
p
n2
(c) lim
+ 2n ;
(i) lim
n→∞
√
√
n+6 n+1− n .
q
40. Korzystając z twierdzenia o trzech ciągach obliczyć granice:
√
2n + (−1)n
⌊nπ⌋
(a) lim
;
(b) lim
;
(c) lim n 3 + sin n;
n→∞
n→∞ n
n→∞
3n + 2
(d) lim
n→∞
r
n
2
3
1
+ 2 + 3;
n n
n
s
(f) lim
n
n→∞
3n + 2n
;
5n + 4n
(e) lim
n→∞
1
1
1
+ 2
+ ... + 2
.
2
n +1 n +2
n +n
41. Korzystając z definicji liczby e oraz z twierdzenia o granicy podciągu obliczyć granice:
(a) lim
n→∞
1
1+
n
3n−2
;
(b) lim
n→∞
5n + 2
5n + 1
15n
;
(c) lim
n→∞
3n
3n + 1
n
;
(d) lim
n→∞
n+4
n+3
5−2n
.
42. Korzystając z twierdzenia o granicach niewłaściwych ciągów obliczyć granice:
n2 + 1
;
n→∞
n
(a) lim
(d) lim
n→∞
n+1
2n
(b) lim
n→∞
n
;
n4 − 3n3 − 2n2 − 1 ;
1 − (n + 1)!
;
n→∞
n! + 2
(e) lim
(c) lim (1 + 2n − 3n );
n→∞
arc tg n
.
n→∞ arc ctg n
(f) lim
Lista 6
43. Korzystając z definicji Heinego granicy właściwej lub niewłaściwej funkcji uzasadnić równości:
1
2
= 0;
(c) lim+
= ∞.
(a) lim (x − 2)5 = 1;
(b) lim
x→∞ x
x→3
x→ 2 x − 2
44. Wskazując odpowiednie dwa ciągi uzasadnić, że podane granice nie istnieją:
j k
√
x2
;
(b) lim x2 ;
(a) lim
(c) lim sin x;
x→∞
x→3 x − 3
x→2
sgn x
1
(e) lim
;
(f) lim (x−⌊x⌋) .
(d) lim cos 2 ;
x→0 sgn (x+1)
x→5
x
x→0−
6
45. Korzystając z twierdzeń o arytmetyce granic funkcji obliczyć granice:
√
x2 − 1
x2 − 4
x+ x
x3 − 1
√
(a) lim 2
;
(b) lim 2
; (c) lim
;
(d) lim 4
;
x→1 x − x + 1
x→2 x − x − 2
x→0
x→1 x − 1
x
√
p
x−2−2
x2 − 5x + 4
2x + 1
; (f) lim
; (g) lim
;
(e) lim
x2 + 1 + x ; (h) lim x
x→∞ x(x − 5)
x→∞ 3 + 2
x→−∞
x→6
x−6
sin2 x
tg2 x + 1
;
(j)
lim
.
(i) lim
2
x→0 1 − cos x
x→ π2 − tg x + 5
46. Zbadać, obliczając granice jednostronne, czy istnieją granice:
1
3
(b) lim 2 x ;
(a) lim x sgn x;
x→0
x→0
x2 − 4
;
x→2 |x − 2|
(c) lim
1
(d) lim x arc tg .
x→0
x
47. Korzystając z twierdzenia o trzech funkcjach uzasadnić równości:
√
1
2−x + sin x
1
(a) lim x cos 2 = 0; (b) lim x3 arc tg = 0; (c) lim −x
= 1;
x→−∞ 2
x→0
x
x
+ cos x
x→0+
48. Korzystając z granic podstawowych wyrażeń nieoznaczonych
1
tg
sin2 3x
x;
(a) lim
;
(b) lim
2
x→∞
x→0
x2
tg
x
cos 5x
1
(d) lim x2 arc tg ;
(e) limπ
;
x→∞
x
x→ 2 cos 3x
√
ln (1 + 2x )
ln (1 + 3 x)
;
(h*) lim
;
(g) lim
x→−∞
x→0
x
3x
1
x
(k) lim [1 + tg(2x)]ctg x ;
(j) lim (1 + 2x) ;
x→0
x→0
(d) lim
x→∞
2+sin x
= 0.
x2
obliczyć granice:
arcsin 2x
;
x→0 arc tg x
(c) lim
e3x − 1
;
x→0 sin 2x
(f) lim
2x − 1
√
;
x→0+ 4 x − 1
√
√
3
1+x− 61−x
(l) lim
.
x→0
x
(i) lim
Lista 7
49. Znaleźć asymptoty pionowe i ukośne funkcji:
x3 + x2
2x3
(a) f (x) = 2
;
(b) f (x) =
;
x −4
(x + 1)2
√
1 + x2
3x
(d) f (x) =
;
(e) f (x) = x
;
x
3 −9
cos x
;
(h) f (x) = x − arc tg x;
(g) f (x) = x
e +1
x−3
;
(c) f (x) = √
x2 − 9
sin2 x
(f) f (x) =
;
x3
1 x
(i*) f (x) = 1 +
.
x
50. Dobrać parametry a, b ∈ R tak, aby podane funkcje były ciągłe na R:

 2

π


 sin x dla |x| ­ ,
 a +1 dla x < −1,
 ax +1 dla x < −1,
2
dla −1 ¬ x ¬ 0,
(b) f (x) =
(c) f (x) = 2x
(a) f (x) = x

 b − 2x dla x ­ −1;

 ax+b dla |x| < π ;
 3
x +bx dla x > 0.
2
51. Określić rodzaje nieciągłości funkcji w punkcie a (jeżeli istnieją) dla funkcji o podanych wykresach:
(a)
(b)
y
(c)
y
y = f (x)
a
x
y
y = f (x)
a
7
x
y = f (x)
a
x
(d)
(e)
y
(f)
y
y = f (x)
y = f (x)
a
y
x
a
y = f (x)
x
a
x
52. Wyznaczyć punkty nieciągłości podanych funkcji i określić ich rodzaj:

x+2




1
 x2 + x + 2 dla x 6= 1, 2

arc tg dla x 6= 0,
(a) f (x) = 0
(b) f (x) =
x
dla x = 1,

0

dla x = 0;

1
dla x = 2;


x2 −1
√
dla x ∈ (0, 1) ∪ (1, ∞),
(c) f (x) =
x−1


3
(d) f (x) =
dla x = 1;
h
i
(e) f (x) = sgn x(x − 1) ;

 |x| + x

(f) f (x) =



x2
dla x 6= 0,
1 − cos
1
dla x 6= 0,
x
dla x = 0.
0
0
dla x = 0;
53. Uzasadnić, że podane równania mają jednoznaczne rozwiązania we wskazanych przedziałach:
5π
π
sin x
3
(a) x + 6x − 2 = 0, [0, 1];
(b) x sin x = 7, 2π,
+ x, 0,
;
(c) 1 =
;
2
2
2
1
,1 ;
(e) 3x + x = 3, [0, 1];
(f) x2x = 1, [0, 1].
(d) x100 + x − 1 = 0,
2
Wyznaczyć rozwiązania równania (a) 0.125.
Lista 8
54*. Korzystając z twierdzenia Weierstrassa o przyjmowaniu kresów uzasadnić, że podane zagadnienia
ekstremalne mają rozwiązania:
(a) wśród stożków wpisanych w kulę o promieniu r istnieje ten, który ma największą objętość;
(b) wśród trójkątów prostokątnych wpisanych w koło o promieniu r istnieje ten, który ma największy
obwód;
(c) wśród prostokątów wpisanych w trójkąt równoboczny o boku a istnieje ten, który ma największe
pole (założyć, że dwa wierzchołki prostokąta należą do ustalonego boku trójkąta).
55. Korzystając z definicji obliczyć pochodne funkcji:
(a) f (x) = x2 − 3x, gdzie x ∈ R;
(c) f (x) =
√
x, gdzie x > 0;
1
, gdzie x 6= −1;
x+1
π
(d) f (x) = tg x, gdzie x 6= + kπ dla k ∈ Z.
2
(b) f (x) =
56. Badając pochodne jednostronne rozstrzygnąć, czy istnieją pochodne podanych funkcji we wskazanych punktach:
(a) f (x) = x2 − x , x0 = 1;
Naszkicować wykresy tych funkcji.
(b) f (x) = sin x · sgn (x), x0 = 0.
57. Zbadać z definicji, czy podane funkcje mają pochodne niewłaściwe w punkcie x0 = 0:
q
√
(c) f (x) = | sin x|.
(a) f (x) = 3 − 5 x;
8
58. Zakładając, że funkcje f i g mają pochodne właściwe na pewnym przedziale, obliczyć pochodne
funkcji:
(a) y = f (x) cos g(x);
(b) y = e
(d) y = ln f (x)g(x) + 1 ;
f (x)
g(x)
;
f (x)
;
(e) y = tg
g(x)
(c) y = arc tg f (x)g(x);
(f) y = f (x) arc tg g(x).
59. Korzystając z reguł różniczkowania obliczyć pochodne funkcji:
x2 + 1
ex+1
(a) y =
;
(b) y = 3 cos x + tg x;
(c) y =
;
sin x
x − 1
√ √ 1
(d) y = x3 + 2 ex ;
(e) y = 1 + 4 x tg x ;
(f) y = ex arc tg x;
x
(g) y = ln sin2 x + 1 ;
2
2sin x
(j) y = cos2 x ;
3
(h) y =
q
3
(i) y = ee ;
x
arcsin (x2 );
tg x
(k*) y = x
;
(l*) y =
√
x
x.
Lista 9
60 (P). Obliczyć f ′ , f ′′ , f ′′′ funkcji:
2
;
x
(a) f (x) = 4x7 − 5x3 + 2x;
(b) f (x) = x3 −
(d) f (x) = arc tg x;
(e) f (x) = sin3 x + cos3 x;
(c) f (x) =
ex
;
x
(f) f (x) = x3 ln x.
61 (P). Napisać równania stycznych do wykresów podanych funkcji we wskazanych punktach:
x
(a) f (x) = arcsin , (1, f (1));
2
√
(d) f (x) = 2x + 1, (3, f (3));
(b) f (x) = ln x2 + e , (0, f (0));
(e) f (x) =
√ √
2x
2,
f
2 ;
,
1 + x2
(c) f (x) = etg x ,
(f*) f (x) =
√
x
π
,f
4
π
4
;
x, (e, f (e)).
62. (a) Napisać równanie stycznej do wykresu funkcji f (x) = x4 − 2x + 5, która jest równoległa do
prostej y = 2x + 3.
√
π
(b) Znaleźć styczną do wykresu funkcji f (x) = x, która tworzy kąt
z dodatnią częścią osi Ox.
4
(c) Znaleźć równanie stycznej do wykresu funkcji f (x) = x ln x, która jest prostopadła do prostej
2x + 6y − 1 = 0.
1
(d) Wyznaczyć równanie stycznej do wykresu funkcji f (x) = x arc tg , w punkcie jego przecięcia z
x
prostą πx = 4y.
63. Korzystając z różniczki funkcji obliczyć przybliżone wartości wyrażeń:
√
1
2001
3
;
(a) 7.999;
(b) √
;
(c) ln
2000
3.98
(e) e0.04 ;
(d) ln 0.9993;
(g)
1
1
33π
+ sin
2
200
;
(h)
2
;
1 + e0.005
(f) arccos 0.499;
(i*) ln 0.2 +
√
1 + 0.04 .
64. (a) Fragment terenu ma kształt trójkąta równoramiennego o boku b = 200 m. Kąt przy wierzπ
chołku tego trójkata, zmierzony z dokładnością 0.01 rad wynosi . Z jaką w przybliżeniu dokładnością
3
można obliczyć pole tego terenu?
9
(b) Objętość kulki metalowej, wyznaczona z dokładnością 1 cm3 , wynosi 36π cm3 . Z jaką w przybliżeniu dokładnością można obliczyć średnicę tej kuli?
(c) Do szybu puszczono swobodnie kamień i zmierzono czas jego spadania z dokładnością 0.1 s. Z
jaką w przybliżeniu dokładnością można wyznaczyć głębokość sztolni, jeżeli czas spadania kamienia
wyniósł 4.1 s? Przyjąć g = 9.8 m/s2 .
(d) Średnica kuli zmierzona z dokładnością 0.1 mm wynosi 21.7 mm. Z jaką w przybliżeniu dokładnością można obliczyć objętość tej kuli?
(e) Przekątna sześcianu zmierzona z dokładnością 1 mm wynosi 14.3 cm. Z jaką w przybliżeniu dokładnością można obliczyć pole powierzchni całkowitej tego sześcianu?
(f) W biegu na 100 m czas mierzy się z dokładnością 0.01 s. Z jaką w przybliżeniu dokładnością można
obliczyć średnią prędkość zawodniczki, jeśli uzyskała ona czas 12.50 s?
65*. Korzystając z twierdzenia Lagrange’a uzasadnić podane nierówności:
y
(a) |arc tg x − arc tg y| ¬ |x − y| dla x, y ∈ R; (b) ln < y − x dla 1 ¬ x < y;
x
x
(c) x ¬ arcsin x ¬ √
dla 0 ¬ x < 1;
(d) ex > ex dla x > 1.
1 − x2
Lista 10
66. Znaleźć przedziały monotoniczności funkcji:
x4 x3
−
− x2 ;
4
3
√
(e) f (x) = x − 3 3 x;
(a) f (x) = x3 − 30x2 + 225x;
(d) f (x) =
(b) f (x) =
x3
;
3 − x2
(g) f (x) = x ln2 x;
(h) f (x) =
(c) f (x) = 4x +
(f) f (x) = xe−3x ;
x
;
ln x
67. Znaleźć wszystkie ekstrema lokalne funkcji:
1
(a) f (x) = x3 − 4x2 ;
(b) f (x) = x + ;
x
√
1
(d) f (x) = 2
;
(e) f (x) = x − x;
x −x
p
(g) f (x) = x ln x;
(h) f (x) = 3x − x3 ;
1
;
x
(i) f (x) =
(c) f (x) =
1
.
x ln x
2x2 − 1
;
x4
(f) f (x) = x2 − 5x − 6 ;
(i) f (x) = 2 arc tg x − ln 1 + x2 .
68. Znaleźć wartości najmniejsze i największe podanych funkcji na wskazanych przedziałach:
1−x
, [0, 1];
(a) u(x) = 2x3 − 15x2 + 36x, [1, 5];
(b) v(x) = arc tg
1+x
(c) w(x) = (x − 3)2 e|x| , [−1, 4];
√
(e) g(x) = x − 2 x, [0, 5];
(d) z(x) = 1 − 9 − x2 , [−5, 1];
3
(f) h(x) = 2 sin x + sin 2x, 0, π .
2
69. (a) Platforma wiertnicza jest zakotwiczona na morzu 10 km od brzegu. Ropa z tej platformy
będzie dostarczana rurociągiem do rafinerii położonej nad brzegiem morza, 16 km od punktu brzegu
najbliższego platformie. Koszt ułożenia 1 km rurociągu na dnie morza wynosi 200 000 euro, a na lądzie
– 100 000 euro. Do którego miejsca na brzegu należy doprowadzić rurociąg, aby koszt jego budowy
był najmniejszy?
b
Platforma
wiertnicza
10 km
b
x
b
b
Rafineria
16 km
10
(b) Jaka powinna być miara kąta α przy wierzchołku trójkąata równoramiennego o danym polu, aby
promień koła r wpisanego w ten trójkąt był największy?
α
r
(c) Prostopadłościenny kontener ma mieć pojemność 22.50 m3 i kwadratową podłogę. Koszt 1 m2
blachy potrzebnej do wykonania jego podłogi i pokrywy wynosi 20 zł, a ścian bocznych – 30 zł. Jakie
powinny być wymiary kontenera, aby koszt jego budowy był najmniejszy?
(d) Jakie powinny być wymiary a, b prostokątnego pola o powierzchni S, którego jednym naturalnym
bokiem jest brzeg rzeki, aby na jego ogrodzenie zużyć jak najmniej siatki?
rzeka
a
S
b
(e) Odcinek o długości l podzielić na dwie części tak, aby suma pól kwadratów zbudowanych na tych
częściach była najmniejsza.
70. Korzystając z reguły de L’Hospitala obliczyć granice:
π
ln sin x
ln (2x + 1)
2 ;
(a) lim
;
(b) lim
x→∞
x→1
x
ln x
ln cos x
x10 − 10x + 9
;
(e) lim
;
(d) lim 5
x→0 ln cos 3x
x→1 x − 5x + 4
x
(g) lim x ln x;
(h) lim (π − x) tg ;
+
−
2
x→0
x→π
1
x
(j) lim (cos x) ;
(k) lim
x→∞
x→0
2
arc tg x
π
x
x − arc tg x
;
x→0
x2
(c) lim
(f) lim x arc ctg x;
x→∞
(i) lim
x→0−
1
− ctg x ;
x
(l) lim (1 + x)ln x .
;
x→0+
Lista 11
71. Określić przedziały wypukłości oraz punkty przegięcia funkcji:
(a) f (x) = x(x − 1)(x − 3);
(d) f (x) = ln 1 + x2 ;
(g) f (x) = sin x +
1
sin 2x;
8
(b) f (x) = xe−x ;
(e) f (x) =
1
;
1 − x2
(h) f (x) = earc tg x ;
x3
;
+ 12
2
(f) f (x) = x − x3 − 4 ln |x|;
3
ln x
(i) f (x) = √ .
x
(c) f (x) =
x2
72. Zbadać przebieg zmienności podanych funkcji i następnie sporządzić ich wykresy:
2
(a) f (x) = (x − 1) (x + 2);
4
4
− 2;
x x
2x
(g) f (x) = xe ;
(d) f (x) = 3 −
x3
(b) f (x) =
;
x−1
p
(e) f (x) = x 1 − x2 ;
(h*) f (x) = sin x + sin 3x;
11
√
x
;
x−1
x
(f) f (x) =
;
ln x
(i) f (x) = x2 ln x.
(c) f (x) =
73. Napisać wzory Taylora z resztą Lagrange’a dla podanych funkcji f , punktów x0 oraz n :
1
(a) f (x) = x3 , x0 = −1, n = 4; (b) f (x) = 2 , x0 = 1, n = 2;
(c) f (x) = sin 2x, x0 = π, n = 3;
x
(d) f (x) = e−x , x0 = 0, n = 5; (e) f (x) = arc tg x, x0 = 0, n = 3; (f) f (x) = ln x, x0 = e, n = 4.
74. Napisać wzory Maclaurina z n-tą resztą Lagrange’a dla funkcji:
x
(b) f (x) = ch x;
(c) f (x) = cos x;
(a) f (x) = sin ;
3
x
.
ex
(d) f (x) =
75. Oszacować dokładności podanych wzorów przybliżonych na wskazanych przedziałach:
π
(a) tg x ≈ x, |x| ¬ ;
(b) cos2 x ≈ 1 − x2 , |x| ¬ 0.1;
12
√
x x2
x2
x3
(c) 1 + x ≈ 1 + − , |x| ¬ 0.25;
(d) ln(1 − x) ≈ −x −
− , |x| < 0.1.
2
8
2
3
76. Stosując wzór Maclaurina obliczyć:
√
1
3
(b) 0.997 z dokładnością 10−3 ;
(a) z dokładnością 10−3 ;
e
(c) ln 1.1 z dokładnością 10−4 ;
(d) sin 0.1 z dokładnością 10−5 .
Lista 12
77. Obliczyć całki nieoznaczone:
(a)
Z √
3
(d)
Z
3
x2
√
1
+ 3 − 2x x
x
(1 − x) dx
√ ;
(b)
1− 3 x
Z 3 √
3
x + x2 − 1
√
(e)
dx;
x
Z
dx;
cos 2x dx
;
cos x − sin x
(c)
Z
x4 dx
;
x2 + 1
(f)
Z
2x − 5x
dx.
10x
78. Korzystając z twierdzenia o całkowaniu przez części obliczyć całki nieoznaczone:
(a)
Z
(e)
Z
(i)
Z
xe−3x dx;
2
x sin x dx;
2x
e
sin x dx;
(b)
Z
x2 2x dx;
(f)
Z
arccos x dx
√
;
x+1
(j)
Z
sin x sin 3x dx;
(c)
Z
(g)
Z
(k)
Z
√
x arc tg
√
x dx;
ln(x + 1) dx;
sin 3x cos x dx;
79. Stosując odpowiednie podstawienia obliczyć całki nieoznaczone:
√
Z
Z
Z √
1 + 4x
cos x
√
dx; (c) (x+1) sin x2 +2x+2 dx;
(a)
dx; (b)
x
x
(e)
Z
dx
;
ch x
(i)
Z
ln x
dx;
x
(f)
Z
(5−3x)
(j)
Z
ex dx
;
e2x + 1
10
dx;
(g)
Z
x
(k)
Z
5 sin x dx
;
3−2 cos x
2
p
5
5x3 +1 dx;
80 (P). Obliczyć całki z ułamków prostych pierwszego rodzaju:
Z
Z
Z
Z
5 dx
dx
8 dx
dx
;
(c)
.
;
(b)
;
(d)
(a)
(x − 3)7
x+5
(2 − 7x)3
9x + 20
12
(d)
Z
x dx
;
cos2 x
(h)
Z
arccos x dx;
(l)
Z
cos x cos 5x dx.
(d)
Z
cos x dx
√
;
1 + sin x
(h)
Z
dx
√ ;
2+ x
(l)
Z
2
x3 ex dx.
81. Obliczyć całki z ułamków prostych drugiego rodzaju:
Z
Z
Z
dx
(6x + 3) dx
(4x + 2) dx
(a)
;
(b)
;
(c)
;
2
2
2
x + 4x + 29
x +x+4
x − 10x + 29
Z
Z
Z
dx
(x − 1) dx
5 dx
;
(e*)
(d)
;
(f*)
.
2
2
9x + 6x + 2
(x2 − 4x + 5)
(x2 + 2)3
82. Obliczyć całki z funkcji wymiernych:
(a)
(x + 2) dx
;
x(x − 2)
Z
(b)
(4x + 1) dx
;
2x2 + x + 1
Z
(5 − 4x) dx
(i)
;
x2 − 4x + 20
(e)
Z
Z
x2 dx
;
x+1
(c)
Z
dx
;
(x − 1)x2
(3x − 1) dx
;
x2 − x + 1
Z
x2 dx
(j)
;
x2 + 2x + 5
(f)
(d)
Z
(x2
2 dx
;
+ 6x + 18
Z
dx
(l)
.
x (x2 + 4)
dx
;
2
x + 2x + 8
Z
x(x + 2) dx
(k)
;
x2 + 2x + 2
Z
(g)
dx
;
+ 1) (x2 + 4)
Z
(h)
Z
x2
Lista 13
83. Obliczyć całki z funkcji trygonometrycznych:
(a)
Z
sin3 x dx;
(b)
Z
sin4 x cos3 x dx;
(c)
Z
(d)
Z
sin3 x cos6 x dx;
(e)
Z
cos2 x cos 2x dx;
(f*)
cos4 x dx;
Z
sin2 2x sin2 x dx.
84. Obliczyć całki z funkcji trygonometrycznych:
Z
Z
Z
1 + tg x
dx
dx
;
(b)
dx;
(c)
;
(a)
sin x + tg x
cos x
1 + 2 cos2 x
(d)
Z
sin2 x dx
;
1 + cos x
(g)
Z
dx
;
cos x
(e)
Z
(h)
Z
dx
;
1 − tg x
dx
;
sin x + cos x
(f)
Z
sin5 x dx
;
cos3 x
(i)
Z
dx
.
3 sin x + 4 cos x + 5
85. Korzystając z twierdzenia Newtona-Leibniza obliczyć całki:
(a)
Z2
x 1+x
Z1
x−1
dx;
x+1
−1
(d)
0
(g)
3
Z2π
dx;
Z2 √
(b)
1
(e)
Z9
0
2
(sin x + cos x) dx;
1
x+ √
x
Z2 (c)
dx;
1
2
1
1
− 2+ 4
3
x
x
x
dx;
1
dx
;
2
x +9
(h)
π
Zπ
(f)
Z2
− 12
2
sin x cos x dx;
0
(i)
Ze
dx
;
−1
x2
x ln x dx.
1
86. Obliczyć całki oznaczone dokonując wskazanych podstawień:
(a)
(d)
0
Z3
Z6
Ze
Zπ
1
cos x
sin xe
dx, cos x = t;
(b)
1
dx
√
, 3x − 2 = t2 ;
1 + 3x − 2
(e)
x dx
√
, 1 + x = t;
x+1
(c)
Z1 √
x 1 + x dx,
√
1 + x = t;
0
1
ln x dx, ln x = t;
(f)
Z4
0
1
13
√
dx
, x = t2 ;
x(1 − x)
(g)
1
2
Z3 p
9 − x2 dx, x = 3 sin t;
0
(g)
Zln 3
0
ex dx
, ex = t;
1 + e2x
(i)
Ze2 √
3
e
1
x − x3 dx
, x= .
4
x
t
87. Metodą całkowania przez części obliczyć całki oznaczone:
(a)
Z1
2x
xe
Z1
0
Ze
√
ln x
dx;
x2
Zπ
Z1
arcsin x dx.
(b)
dx;
−1
π
4
(d)
Z
x sin 2x dx;
(e)
0
2 2x
x e
(c)
dx;
x(1 + cos x) dx;
(f)
0
e
0
88. Obliczyć całki oznaczone:
(a)
Z2
1
e
(c)
(e)
Z2
−2
Z2
−2
(x − 1)sgn (ln x) dx;
||x| − 1| dx;
(b)
0
(d)
sgn x − x2 dx;
Z3
(f)
Z4
0
Z3
1


 1−x
dla 0 ¬ x ¬ 1,
f (x) dx, gdzie f (x) = 1
dla 1 < x ¬ 2,

 (2−x)2 dla 2 < x ¬ 3;
|x − 1| dx
;
|x − 2| + |x − 3|
x ⌊x⌋ dx.
Lista 14
89. Obliczyć pola obszarów ograniczonych krzywymi:
1
(a) y = 2x − x2 , x + y = 0; (b) y = x2 , y = x2 , y = 3x;
2
8
2
x, y=2, x=0
(d) 4y = x , y = 2
;
(e) y = 2
;
x +4
(g) y = πx2 , x = πy 2 ;
(h) yx4 = 1, y = 1, y = 16;
90 (P). Obliczyć pola trapezów krzywoliniowych:
(a)
y
(b) y
y = −4x2 + 4x + 6
(c)
1
, y = x, y = 4;
x2
(f) y = x + sin x, y = x, (0 ¬ x ¬ 2π);
(c) y =
(i) y 2 = −x, y = x − 6, y = −1, y = 4.
y
y=x
y=3
y = 3x2 − 6x + 1
x
x
(d)
x
y = 4x2 − 8x
(e) y
x = 8 − y2
y
x=3
x = y 2 − 2y
y = −3x2 + 3x + 7
x = y2
x
x
14
(f) y
y = 2−x
x = y2
x
91. Obliczyć długości krzywych:
√
(a) y = 2 x3 , gdzie 0 ¬ x ¬ 11;
(c) y = ln
ex
ex
(b) y = ch x, gdzie 0 ¬ x ¬ 1;
+1
, gdzie 2 ¬ x ¬ 3;
−1
(d) y = 1 − ln cos x, gdzie 0 ¬ x ¬
π
.
4
92. Obliczyć objętości brył powstałych z obrotu figur T wokół wskazanych osi:
√
2
(a) T : 0 ¬ x ¬ 2, 0 ¬ y ¬ 2x − x2 , Ox;
(b) T : 0 ¬ x ¬ 5, 0 ¬ y ¬ √
, Oy;
2
x +4
√
1
(d) T : 1 ¬ x ¬ 3, 0 ¬ y ¬ , Oy;
(c) T : 0 ¬ x ¬ 1, x2 ¬ y ¬ x, Oy;
x
4
π
(e) T : 1 ¬ x ¬ 4,
¬ y ¬ 5−x, Ox;
(f) T : 0 ¬ x ¬ , 0 ¬ y ¬ sin x+cos x, Ox.
x
2
93. Obliczyć pola powierzchni powstałych z obrotu wykresów podanych funkcji wokół wskazanych
osi:
√
x−1
, 1 ¬ x ¬ 10, Oy;
(b) f (x) = 4 + x, −4 ¬ x ¬ 2, Ox;
(a) f (x) =
p9
(d) f (x) = |x − 1| + 1, 0 ¬ x ¬ 2, Oy;
(c) f (x) = 4 − x2 , −1 ¬ x ¬ 1, Ox;
2
√
π
x
(f) f (x) = cos x, 0 ¬ x ¬ , Ox.
(e) f (x) =
, 0 ¬ x ¬ 3, Oy;
2
2
Lista 15
94. Korzystając z definicji zbadać zbieżność całek niewłaściwych pierwszego rodzaju:
(a)
Z∞
1
(d)
dx
;
(x + 2)2
(b)
dx
;
+4
(e)
Z0
−∞
x2
Z∞
x sin x dx;
π
Z∞
(c)
3
x2 e−x dx;
(f)
−∞
Z∞
1
Z∞
√
3
dx
;
3x + 5
x2
−∞
dx
.
−4x + 13
95. Korzystając z kryterium ilorazowego zbadać zbieżność całek niewłaściwych pierwszego rodzaju:
Z∞ √
Z∞
Z∞
x dx
1
x dx
√
√
(a)
;
(c) sin2 dx;
;
(b)
2
5
x+x
x
x −3
1
(d)
Z0
1
5
−∞
x−1
;
3
x +x+1
(e)
Z∞
1
x2 dx
x3 − sin x
;
(f*)
Z−1
−∞
e2x + 1 dx
.
ex − 1
96. Korzystając z kryterium porównawczego zbadać zbieżność całek niewłaściwych pierwszego rodzaju:
(a)
(d)
Z∞
10
Z∞
0
dx
√
;
x−3
x dx
√
;
3
x7 + 1
Z∞
(x − 1) dx
(b)
;
x4 + x + 1
2 √
Z∞
2 + cos x dx
√
(e)
;
x−1
(c)
Z∞
π
(f*)
(1 + sin x) dx
;
x3
Z0
−∞
2
15
2x dx
.
x−1