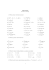Wn. 1. Lista caªek funkcji elementarnych

Def. 1.
funkcj¦
Funkcj¡ pierwotn¡
F,
x∈I
która dla
funkcji
f
na danym przedziale
I
nazywamy dowoln¡
speªnia warunek
F 0 (x) = f (x).
Przykªad:
1.
zawiera j¡cym
f (x) = √
0.
sgnx nie ma funkcji
arcsin i − arccos
Funkcje
1
.
1 − x2
Niech
Tw. 1.
1.
Funkcja
Zachodzi jednak:
pierwotnej na »adnym przedziale
s¡ funkcjami pierwotnymi funkcji
arcsin x = − arccos x +
π
2.
F b¦dzie funkcj¡ pierwotn¡ funkcji f na przedziale I . Wówczas:
G(x) = F (x) + C jest funkcj¡ pierwotn¡ funkcji f na I dla dowolnej staªej
C ∈ R,
2. Ka»d¡ funkcj¦ pierwotn¡ mo»na zapisa¢ w postaci
Ka»da funkcja ci¡gªa na
Tw. 2.
Uwaga
F (x) + C .
I ma funkcj¦ pierwotn¡ na I .
1. Nie ka»da funkcja pierwotna danej funkcji elementarnej jest elemen-
tarna! Przykªadowo:
Def. 2.
ex
2
,
sin x √
,
1 + x3 , cos x2 .
x
Caªk¡ nieoznaczon¡
funkcji
f
nazywamy zbiór funkcji:
Z
f (x)dx := {F (x) + C : C ∈ R},
gdzie
F
jest dowoln¡ funkcj¡ pierwotn¡. Piszemy krótko:
Wn. 1.
2.
R
1.
R
f (x)dx = F (x) + C .
[ f (x)dx]0 = f (x),
R
f 0 (x)dx = f (x) + C .
Lista caªek funkcji elementarnych
1.
2.
R
0dx = C ,
R
xr dx =
Z
3.
Z
4.
5.
R
+C
dla
r 6= −1,
dx
= ln |x| + C ,
x
ax dx =
ax
+C
ln a
dla
0 < a 6= 1,
sin xdx = − cos x + C ,
Z
dx
= −ctgx + C ,
sin2 x
Z
dx
= arctgx + C ,
1 + x2
6.
7.
xr+1
r+1
R
Z
(
R
ex dx = ex + C
cos xdx = sin x + C ,
dx
= tgx + C ,
cos2 x
1
),
Z
8.
9.
10.
dx
= arcsin x + C ,
1 − x2
R
R
shx = chx + C , chxdx = shx + C ,
Z
Z
dx
dx
=
−cthx
+
C
,
= thx + C .
2
sh x
ch2 x
√
f i g maj¡ funkcje pierwotne, to
R
R
1. (f (x) ± g(x))dx = f (x)dx + g(x)dx,
R
R
2.
cf (x)dx = c f (x)dx.
Tw. 3.
Je»eli
R
Przykªady:
Z
1.
2.
3.
1. Wyznaczy¢ caªki:
x2 − x + 1
√
dx
x
R
ctg2 xdx
R
3x 5−2x dx
Caªkowanie przez cz¦±ci
f i g maj¡ ci¡gªe pochodne, to
Z
0
f (x)g (x)dx = f (x)g(x) − f 0 (x)g(x)dx.
Tw. 4 (O caªkowaniu przez cz¦±ci).
Z
Przykªady:
2.
3.
R
ln xdx
R
sin xex dx
Z
4.
2.
1.
R
Je»eli
x sin xdx
dx
(1 + x2 )2
Wzór rekurencyjny:
Z
dx
x
2n − 1
=
+
(a2 + x2 )n+1
2na2 (a2 + x2 )n
2na2
2
Z
dx
(a2 + x2 )n
Caªkowanie przez podstawienie
Tw. 5 (O caªkowaniu przez podstawienie).
Z
Je»eli
R
f (t)dt = F (t) + C, to
f (ϕ(x))ϕ0 (x)dx = F (ϕ(x)) + C.
f i ϕ0 zakªadamy, »e s¡ ci¡gªe.)
R
Wn. 2. Je»eli
f (x)dx = F (x) + C i a 6= 0, to
Z
1
f (ax + b)dx = F (ax + b) + C.
a
(O
Wn. 3.
Przykªady:
Z
2.
3.
R
Z
4.
5.
6.
3.
1.
R
(2x − 5)7 dx
dx
1
x
= arctg + C
a2 + x2 a
a
cos3 xdx
dx
√ dx
2+ x
R√
R
f 0 (x)
dx = ln |f (x)| + C.
f (x)
Z
a2 − x2 dx=
1 p 2
x
[x a − x2 + a2 arcsin ] + C
2
a
cos4 xdx
Przydatne wzory trygonometryczne
cos2 x =
1 − cos 2x
1 + cos 2x
; sin2 x =
2
2
Uªamki proste
I:
A
,
(x − a)n
II :
Bx + C
(∆ < 0)
(px2 + qx + r)n
Tw.
6 (O rozkªadzie funkcji wymiernej na uªamki proste). Ka»da funkcja
wymierna wªa±ciwa rozkªada si¦ jednoznacznie na sum¦ uªamków prostych.Je»eli
w mianowniku wyst¦puje czynnik (x − a)n , to w rozkªadzie nale»y uwzgl¦dni¢:
A1
A2
An
+
+ ... +
.
x − a (x − a)2
(x − a)n
Je»eli w mianowniku wyst¦puje czynnik
uwzgl¦dni¢:
(px2 + qx + r)n , to w rozkªadzie nale»y
B1 x + C 1
B2 x + C2
Bn x + Cn
+
+ ... +
.
px2 + qx + r (px2 + qx + r)2
(px2 + qx + r)n
3
Przykªady:
Z
2.
x2
Z
4.
Z
1.
A
dx = A ln |x + a| + C
x+a
A
A
dx= −
+C
n
(x + a)
(n − 1)(x + a)n−1
Z
3.
4.
4x
dx
+ 2x + 5
x3 + x + 1
dx
x4 + x2
4