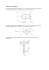Obliczanie geometrycznych momentów bezwładności figur płaskich

OBLICZANIE GEOMETRYCZNYCH MOMENTÓW
BEZWŁADNOŚCI FIGUR PŁASKICH,
TWIERDZENIE STEINERA – LABORATORIUM RACHUNKOWE
Przy obliczeniach wytrzymałościowych dotyczących niektórych przypadków
obciążenia (np. zginanie) potrzebna jest znajomość pewnych wielkości geometrycznych
charakteryzujących przekroje poprzeczne prętów. Wielkościami tymi są momenty
bezwładności względem osi, moment względem układu osi, nazywany również
momentem dewiacji lub odśrodkowym oraz momenty biegunowe.
Moment bezwładności Ax figury płaskiej względem osi x nazywamy sumę
iloczynów elementarnych pól dA tego pola przez kwadrat odległości tych pól od osi x
(rys.1).
Momenty bezwładności:
- osiowe momenty bezwładności Jx, Jy (względem prostej lub osi).
- biegunowy moment bezwładności JO (moment bezwładności względem
ustalonego punktu O, zwanego często biegunem),
- dewiacyjny moment bezwładności Jxy (zboczeniowy moment lub
odśrodkowy) – moment bezwładności względem układu osi.
Rys.1. Oznaczenie elementarnego pola dA.
Jednostką wymiarową momentów bezwładności jest m4. Momenty osiowe oraz
moment biegunowy są zawsze dodatnie, natomiast moment dewiacyjny może być
dodatni lub ujemny lub równy zero.
1
Definicja momentów bezwładności:
1. Osiowe momenty bezwładności
J x = ∫ y 2 dA
J y = ∫ x 2 dA
A
A
2. Biegunowy moment bezwładności
Moment bezwładności biegunowy figury płaskiej względem początku układu
prostokątnego równa się sumie momentów bezwładności względem dwu osi układu
leżącego w płaszczyźnie figury.
J 0 = ∫ ρ 2 dA = ∫ ( x 2 + y 2 )dA = ∫ x 2 dA + ∫ y 2 dA =J y + J x
A
A
A
A
3. Moment dewiacyjny (zboczenia, odśrodkowy)
J xy = ∫ xydA
A
Momenty bezwładności względem osi równoległych.
Twierdzenie Steinera
Przesuńmy prostokątny układ współrzędnych w stosunku do pierwotnie
przyjętego Oxy o składowe przesunięcia a, b.
Znając dla pierwotnego układu osi momenty bezwładności Jx, Jy i moment
dewiacyjny Jxy – wyznacza się dla nowego układu momenty Jxc, Jyc i Jxcyc.
Rys.2. Oznaczenie do wzoru Steinera.
W przypadku gdy początek układu xy pokrywa się ze środkiem ciężkości figury,
momenty statyczne są równe zero i twierdzenie Steinera można przedstawić:
J xc = J x + Aa 2
J yc = J y + Ab 2
J xcyc = J xy + Aab
2
Moment bezwładności figury płaskiej względem osi odległej od środka ciężkości o
a jest równy momentowi bezwładności względem osi równoległej przechodzącej przez
środek ciężkości, zwiększonemu o iloczyn całej powierzchni figury przez kwadrat
odległości a (Aa2).
Twierdzenie Steinera umożliwia obliczanie momentów bezwładności figur
płaskich względem osi równolegle przesuniętych w stosunku do osi centralnych
(osi przechodzących przez środek ciężkości przekroju).
Momenty bezwładności figur złożonych
bezwładności prostych figur składowych.
są
sumą
momentów
Figura złożona może składać się z figur „pełnych” oraz „pustych”. Przy
sumowaniu momentów bezwładności figury „puste” uważa się za figury z ujemnymi
polami powierzchni.
Rys.3. Podział figury złożonej na figury proste
(jeden z możliwych do zastosowania podziałów figury).
3
Definicja momentu statycznego w układzie osi X i Y.
Rys.4. Definicja momentu statycznego
W zależności od położenia przekroju względem osi układu współrzędnych mogą
przyjmować wartości dodatnie i ujemne.
Wykorzystując znane ze statyki pojęcie środka sił, dla środka ciężkości można
napisać:
Obliczanie współrzędnych środka ciężkości figur płaskich.
Przy wykorzystaniu definicji momentów statycznych figur płaskich współrzędne środka
ciężkości figury płaskiej obliczymy ze wzorów:
xc =
Sy
A
yc =
Sx
A
Przydatne twierdzenia do obliczania współrzędnych środka ciężkości figury płaskiej:
- gdy figura płaska ma oś symetrii, to środek ciężkości leży na tej osi,
- jeżeli figura płaska ma dwie osie symetrii, to środek ciężkości leży w punkcie
przecięcia tych osi.
4
Jeżeli przekrój składa się z n części o znanych polach powierzchni Ai oraz
współrzędnych środków ciężkości xi i yi to współrzędne środka ciężkości oblicza się ze
wzorów.
n
n
xc =
∑A ⋅x
i
i =1
i
n
∑A
i =1
yc =
i
∑A ⋅ y
i
i =1
i
n
∑A
i =1
i
Przykład [3]
Określić położenie środka ciężkości figury przedstawionej
na rysunku.
Przekrój podzielono na trzy prostokąty o następujących
polach powierzchni:
A1 = 1⋅1 = 1 cm2,
A2 = 2⋅5 = 10 cm2,
A3 = 2⋅2 = 4 cm2.
Współrzędne środka ciężkości całej figury wynoszą
Celem laboratorium jest wyznaczenie osiowych momentów
bezwładności Jx i Jy oraz dewiacyjnego momentu bezwładności Jxy
Kolejność postępowania przy wyznaczaniu położenia głównych centralnych osi
bezwładności i wartości głównych centralnych momentów bezwładności:
- przyjęcie początkowego układu osi współrzędnych Oxy.
- podział figury na proste figury składowe,
- obliczenia pola powierzchni i wyznaczenie środków ciężkości figur składowych,
- obliczenia pola powierzchni i wyznaczenie położenia środka ciężkości pola całej figury,
- wyznaczenie osiowych momentów bezwładności Jx i Jy oraz dewiacyjnego momentu
bezwładności Jxy.
5
Literatura:
[1] Dyląg Zdzisław, Jakubowicz Antoni, Orłoś Zbigniew, Wytrzymałość materiałów.
Tom I, WNT, 2007.
[2] Niezgodziński Michał E., Niezgodziński Tadeusz Wytrzymałość materiałów,
Wydawnictwo Naukowe PWN, 2010.
[3] Ostwald Marian, Podstawy mechaniki, Politechnika Poznańska; e-skrypty:
www.sms.am.put.poznan.pl/eskrypty_pliki/podstawymechaniki/9momentybezwladnos
cifigurplaskich.pdf
6
7