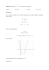Pochodna funkcji Izolda Gorgol - Informacje dla uzytkowników

Pochodna funkcji
Izolda Gorgol
Iloraz różnicowy
Niech x0 ∈ R oraz niech funkcja f będzie określona przynajmniej na przedziale (x0 − r, x0 + r), gdzie r > 0.
DEFINICJA Ilorazem różnicowym funkcji f w punkcie x0 odpowiadającym przyrostowi h, gdzie 0 < |h| < r,
nazywamy liczbę
f (x0 + h) − f (x0 )
.
h
Interpretacja geometryczna ilorazu różnicowego.
Iloraz różnicowy jest równy tangensowi kąta nachylenia siecznej przechodzącej przez punkty (x0 , f (x0 )) oraz (x0 +
h, f (x0 + h)) do dodatniej półosi Ox.
Pochodna funkcji w punkcie
Niech x0 ∈ R oraz niech funkcja f będzie określona przynajmniej na przedziale (x0 − r, x0 + r), gdzie r > 0.
DEFINICJA Jeśli istnieje skończona granica
lim
h→0
f (x0 + h) − f (x0 )
,
h
to nazywamy ją pochodną funkcji f w punkcie x0 i oznaczamy f 0 (x0 ).
Mówimy wtedy, że funkcja f jest różniczkowalna w punkcie x0 . Jeżeli granica ilorazu różnicowego w punkcie x0
nie istnieje lub jest nieskończona, to mówimy, że funkcja f nie jest różniczkowalna w punkcie x0 .
Interpretacja geometryczna pochodnej
Pochodna funkcji w punkcie x0 jest równa tangensowi kąta nachylenia stycznej do wykresu funkcji f w punkcie
(x0 , f (x0 )) do dodatniej półosi Ox.
Równanie stycznej do wykresu funkcji f w punkcie (x0 , f (x0 )):
y = f 0 (x0 )(x − x0 ) + f (x0 ).
Pochodna funkcji na przedziale
Funkcja ma pochodną na przedziale P otwartym wtedy i tylko wtedy, gdy ma pochodną w każdym punkcie tego
przedziału. Funkcję określoną na przedziale P , której wartości w punktach x tego przedziału są równe f 0 (x) nazywamy
pochodną funkcji f na przedziale P i oznaczamy symbolem f 0 .
f 0 : x 7−→ f 0 (x),
x∈P
Działania arytmetyczne na pochodnych funkcji
TWIERDZENIE Jeżeli funkcje f i g są różniczkowalne w punkcie x0 , to:
— (f + g)0 (x0 ) = f 0 (x0 ) + g 0 (x0 );
— (f − g)0 (x0 ) = f 0 (x0 ) − g 0 (x0 );
— (f · g)0 (x0 ) = f 0 (x0 )g(x0 ) + f (x0 )g 0 (x0 );
0
f
f 0 (x0 )g(x0 ) − f (x0 )g 0 (x0 )
—
(x0 ) =
, o ile g(x0 ) 6= 0.
g
g 2 (x0 )
WNIOSEK Jeżeli funkcja f jest różniczkowalne w punkcie x0 , zaś c ∈ R, to
— (cf )0 (x0 ) = cf 0 (x0 ).
1
Twierdzenie o pochodnej funkcji złożonej
TWIERDZENIE Jeżeli funkcja f jest różniczkowalna w punkcie x0 oraz funkcja g jest różniczkowalna w punkcie
f (x0 ), to funkcja g ◦ f jest różniczkowalna w puncie x0 oraz
(g ◦ f )0 (x0 ) = g 0 (f (x0 ))f 0 (x0 ).
Postać logarytmiczno–wykładnicza funkcji
UWAGA Każdą funkcję złożoną postaci [f (x)]g(x) można przedstawić w postaci logarytmiczno–wykładniczej:
[f (x)]g(x) = eg(x) ln f (x)
Postać logarytmiczno–wykładniczą stosujemy do obliczania pochodnych funkcji danych w postaci [f (x)]g(x) .
Pochodne ważniejszych funkcji elementarnych
—
—
—
—
—
—
—
—
—
—
—
—
0
(c) = 0, c ∈ R
(xp )0 = pxp−1 , p ∈ R, zakres zmienności x zależy od p
1 0
1
(√
x ) = − x2 , x ∈ R − {0}
1
0
( x) = 2√
, x ∈ R+
x
0
(sin x) = cos x, x ∈ R
(cos x)0 = − sin x, x ∈ R
(tgx)0 = cos12 x , x 6= π2 + kπ, k ∈ Z
(ctgx)0 = − sin12 x , x 6= kπ, k ∈ Z
(ax )0 = ax ln a, a > 0, x ∈ R
(ex )0 = ex , x ∈ R
1
(loga x)0 = x ln
a , a > 0, a 6= 1, x > 0
1
0
(ln x) = x , x > 0
Twierdzenie o pochodnej funkcji odwrotnej
TWIERDZENIE Niech x0 ∈ Df . Niech f będzie funkcją ciągłą i różnowartościową w otoczeniu punktu x0 oraz
taką, że f 0 (x0 ) 6= 0. Wówczas
1
(f −1 )0 (y0 ) = 0
, gdzie y0 = f (x0 )
f (x0 )
Pochodne funkcji cyklometrycznych:
—
—
—
—
1
(arcsin x)0 = √1−x
, |x| < 1
2
1
0
(arccos x) = − √1−x2 , |x| < 1
1
(arctg x)0 = 1+x
x∈R
2,
1
0
(arcctg x) = − 1+x
x∈R
2,
2