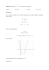1 Badanie przebiegu zmiennosci funckji

przygotowala Joanna Grabowska na podstawie Szymański, Dróbka “Matematyka w szkole średniej. Powtórzenie i zbiór zadań” oraz Leksiński, Nabialek, Żakowski “Matematyka, definicje, twierdzenia, przyklady, zadania”
1
1.1
Badanie przebiegu zmienności funckji
Algorytm badania wykresu funkcji
1) Wyznaczamy dziedzine funkcji f;
2) wyznaczamy granice funkcji na końcach przedzialów, z których sklada sie
dziedzina;
3) znajdujemy miejsca zerowe funkcji f i punkt, w którym wykres przecina
oś y;
4) wyznaczamy pochodna funkcji f i znajdujemy miejsca zerowe pochodnej;
5) znajdujemy przedzialy monotoniczności funkcji i jej ekstrema (jeśli istnieja);
6) badamy, czy istnieja asymptoty wykresu funkcji i znajdujemy ich rónania;
7) wykorzystujac dane zebrane w pkt 1-6 budujemy tabele zmienności i szkicujemy wykresy funkcji f
1.2
Asymptoty wykresu funkcji
Jeśli funkcja f jest określona w przedziale (α, +∞) i istnieje skończone granica limx→+ f (x) = b, to prosta o równianiu y = b nazywamy asymptota pozioma wykresu funkcji f w plus nieskończoności. Podobnie jeśli
funkcja f jest określona w przedzxiale (−∞, α) i istnieje skończona granica limx→− f (x) = b to prosta o równaniu y = b nazywamy asymptota
pozioma funkcji f w minus nieskończoności. Jeśli prosta o równaniu y = b
jest asymptota pozioma wykresu funkcji f zarówno w plus, jak i w minus
niekończoności, to nazywamy ja asymptota pozioma obustronna. Jeśli prosta o równaniu y = b jest asymptota pionowa wykresu funkcji f, to wykres
funkcji zbiliża sie do tej prostej, gdy x daży do nieskończoności.
Jeśli funkcja f jest określona w przedziale (α, +∞) i istnieje skończone
granica limx→a+ f (x) = b, lub limx→a+ f (x) = −∞ to prosta o równianiu
x = a nazywamy asymptota prawostronna pionowa wykresu funkcji f w plus
nieskończoności. Podobnie określamy asymptote lewostronna. Jeśli prosta
jest jednocześnie asymptota pionowaprawo i lewostronnato jest asymptota
pionowa obustronna.
1.3
Monotoniczność funkcji
Jeśli funkcja f jest określona i różniczkowalna w przedziale (a,b) i przy tym
jest funkcja rosnaca w tym przedziale, to jej pochodna f’ jest w każdym
1
punkcie przedzialu (a,b) nieujemna.
Jeśli funkcja f jest określona i różniczkowalna w przedziale (a,b) i przy
tym jest funkcja malejaca w tym przedziale, to jej pochodna f’ jest w każdym
punkcie przedzialu (a,b) niedodatnia.
Jeśli funkcja f jest określona i różniczkowalna w przedziale (a,b), a jej
pochodna f’ przyjmuje co najwyżej skończonej liczbie punktów przedzialu
wartość zero, a we wszystkich pozostalych punktach przedzialu jest dodatnia, to funkcja f jest w przedziale (a,b) rosnaca.
Jeśli funkcja f jest określona i różniczkowalna w przedziale (a,b), a jej
pochodna f’ przyjmuje co najwyżej skończonej liczbie punktów przedzialu
wartość zero, a we wszystkich pozostalych punktach przedzialu jest ujemna,
to funkcja f jest w przedziale (a,b) malejaca.
1.4
Ekstremum funkcji
Zalóżmy, że funkcja f jest określona w przedziale (a, b) i x0 ∈ (a, b). Mówimy,
że funkcja f osiaga w punkcie x0 maksimum, jeśli istnieje taki przedzial
(a1 , b) ⊂ (a, b) o środku w punkcie x0 to dla każdego x ∈ (a1 , b) ix 6= x0 zachodzi nierówność f (x) < f (x0 ). Analogicznie określamy minimum funkcji.
Ekstrema funkcji to minimum lub maksimum funkcji.
2
Przyklad badania zmienności funkcji
2.1
Zadanie 1
Zbadamy przebieg zmiennościo funkcji f określanej wzorem f (x) =
x3 +4
x2
3
4
1) df = (−∞, 0) i (0, +∞) 2) limx→+∞ ( x x+4
2 ) = limx→+∞ (x+ x2 ) = +∞
3
limx→−∞ ( x x+4
2 ) = −∞
3
3
x +4
limx→0+ ( x x+4
2 ) limx→0− ( x2 ) = limx→+∞ (x +
3) f (x) = 0 ⇔ x3 + 4 = 0 i X 2 6= 0 ⇔ x = −
wiec wykres funkcji nei przecina osi y;
4) f ′ (x) =
(x3 +4)′ x2 −(x3 +4)(x2 )′
x4
=
x4 −8x
x4
f ′ (x) = 0 ⇔ x4 − 8x = 0 i x4 6= 0 ⇔ x = 2
5) przedzialy monotoniczności funkcji f:
2
4
)
x2
√
3 4,
= +∞
a ponieważ 0 ∈
/ Df ,
f ′ (x) > 0 ⇔ x(x − 2) > 2 i x 6= 0
< 0 ⇔ x(x − 2) < 2 i x 6= 0
f ′ (x)
stad otrzymujemy:
f ′ (x) > 0 ⇔ x ∈ (−∞, 0) i x ∈ (2, ∞)
f ′ (x) < 0 ⇔ x ∈ (0, 2)
Zatem funkcja rośnie w przedzialach (−∞, 0) i (2, ∞) i maleje w przedziale (0, 2). W takim razie wynika,że f osiaga maksimum w punkcie x0 = 2
i fmin = 3
6) Poniewqaż nie istnieje skończona granica funkcji w nieskończoności ani
granica w minus nieskończoności, to nie istnieje pozioma asymptota wykresu
funkcji f.
Istnieje natomiast asymptota pionowa, jest nia prosta o równaniu x = 0.
Aby zbadać istnienie asymptoty pochylej, najpierw badamy istnbienie
f (x3 +4)
. Granica ta istnieje i wynosi
granicy limx→−∞ f (x)
x , czyli limx→−∞
x3
1. Znaczy to, że wspólczynnik kierunkowy ewentualnej asymptoty jest równy
3
1. Teraz badamy istnienie granicy limx→−∞ ( f (xx2+4) − x). Granica ta wynosi zero. W takim razie asymptota pochyla jest prosta o równianiu x=y.
7) Wykorzystujac zebrane o funkcji wiadomości, budujemy tabele zmienności
funkcji, a nastepnie szkicujemy wykres.
|x
(−∞, 0) 0 (0, 2) 2 (2, ∞)
f ′ (x)
(+)
x (−) 0 (+)
′
f (x)
(↑)
x (↓) 3
(↑)
2.2
Zadanie 2
Zbadać funkcje: y =
x−1 x1
x e
Rozwiazanie: Dziedzina funkcji: Df = (−∞, 0) i (0.∞) Mamy nastepnie
y → 1, gdy x → −∞ lub x → ∞, y → −∞, gdy x → 0− oraz
1
x
limx→0+ y = limx→0+ x−1
x e
−1
limu→∞ 1−u
eu =H limu→∞ eu = 0
1
, gdzie u = x
Z przeprowadzonych obliczeń granic wynika, że wykres funkcji ma lewostronna asymptote pionowa o równaniu x= 0, oraz obustronna asymptote
pozioma y = 1. Wynika stad, że nie istnieje żadna asymptota ukośna.
1
Obliczamy pierwsza pochodna y ′ = 2x−1
e− x . Ponieważ Df ′ = Df ,
x3
y ′ = 0 wtedy i tylko wtedy, gdy x = 21 oraz pochodna zmienia znak w punkcie
x = 12 z ujemnego na dodatni, wiec funkcja w tym punkcie ma ekstremum,
3
minimum; ym in = y( 21 ) = −1
. Ponieważ y ′ > 0 na przedziale (−∞, 0) i na
e2
1
przedziale ( 2 , ∞), wiec funkcja jest na tych przedzialach rosnaca. Ponieważ
y ′ < 0 na przedziale (0, 12 ), wiec funkcja jest malejaca na tym przedziale.
na podstawie uzyskanych informacji sporzadzamy tabelke zmienności
funkcjii sporzadzamy wykres.
(−∞, 0) 0 (0, 12 ) ( 12 ) ( 12 , ∞)
(+)
x (−)
0
(+)
−1
′
(↑)
f (x)
(↑)
x (↓) ( e2 )
|x
f ′ (x)
4