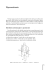DODATEK 1

DODATEK 1
Pole elektryczne nieskończenie wielkiej płaszczyzny z równomiernie rozłożonym
na niej ładunkiem powierzchniowym
W celu wyznaczenia natężenia pola elektrycznego E i potencjału ϕ lub różnicy potencjałów
U = ∆ϕ nieskończenie wielkiej płaszczyzny naładowanej dodatnim ładunkiem rozłożonym
równomiernie z gęstością powierzchniową qs (qs > 0 i qs = const) należy zdefiniować powierzchnię Gaussa, na której zostanie określony strumień wektora natężenia pola elektrycznego Φ. Rozpatrywaną sytuację pokazano na rys. D1.1.
z
2
E2
dS
dS
1
dS
dS
y
dS
E1
x
0
90°
qs
A
.
B
x1
x2
.
Rys. D1.1. Nieskończenie wielka płaszczyzna równomiernie naładowana
ładunkiem powierzchniowym i jej pole elektryczne
Ze względu na nieskończenie wielką płaszczyznę rysuje się dwie płaszczyzny (1) i (2)
równoległe i równoodległe od niej z dwoma elementami powierzchni dS współosiowymi z takim samym elementem na powierzchni rozpatrywanej. W ten sposób otrzymuje się walec o
podstawach równych dS.
Wektory natężenia pola elektrycznego E są wszędzie na wszystkich trzech płaszczyznach
prostopadle do nich, a ze względu na taką samą odległość powierzchni (1) i (2) od rozpatrywanej powierzchni wektory te mają takie same długości, lecz są przeciwnie zwrócone
E1 = −E 2 i E1 = E2 = E .
(D1.1)
Strumień wektora indukcji elektrycznej Ψ (D = ee0E) przez powierzchnię zamkniętą walca jest równy ładunkowi dQ = qs dS obejmowanemu przez tę powierzchnię. Strumień przez
pobocznicę walca jest równy zeru, ponieważ na pobocznicy nie istnieje składowa normalna
wektora E = En = 0. Zatem istnieją tylko dwa strumienie wektora natężenia pola elektrycznego Φ1 i Φ2 przez obie podstawy walca, których powierzchnie są powierzchniami Gaussa. Zatem całkowity strumień Φ jest sumą strumieni składowych Φ1 i Φ2
dΦ = dΦ1 + dΦ 2 = E1dS + E2dS = 2 EdS =
dQ
εε 0
.
(D1.2)
Ponieważ dQ = qs dS, zatem
E=
qs
q
i D= s .
2εε 0
2
(D1.3)
Natężenie pola elektrycznego E nieskończenie wielkiej płaszczyzny naładowanej ładunkiem powierzchniowym o stałej gęstości jest stałe – nie zależy od odległości od płaszczyzny.
Potencjał w polu naładowanej nieskończenie wielkiej płaszczyzny oblicza się ze wzoru
(2.30) dla przypadku jednowymiarowego – jednej zmiennej niezależnej x
E=−
dϕ
.
dx
(D1.4)
Potencjał ϕ w polu płaszczyzny wynosi
ϕ = − ∫ E dx = − ∫
qs
q
dx = − s x + C
2εε 0
2εε 0
(D1.5)
z dokładnością do stałej całkowania, którą należy zdefiniować na podstawie warunku brzegowego. Warunek ten jest następujący: na nieskończenie małej powierzchni (dS = 0), czyli w
punkcie na płaszczyźnie (x = 0) o stałej gęstości powierzchniowej ładunek dQ (dQ = 0) jest
nieskończenie mały, skąd wynika, że potencjał ϕ płaszczyzny musi być równy zero. Zatem
warunek brzegowy wynosi
ϕ = 0 dla x = 0 .
(D1.6)
Ze wzoru (D1.5) wynika, że stała całkowania C = 0 i
ϕ=−
qs
x,
2εε 0
(D1.7)
czyli dla dodatniego ładunku płaszczyzny potencjał maleje z odległością od płaszczyzny.
Można pokazać, że potencjał maleje z odległością wyznaczając różnicę potencjałów ϕ1 i
ϕ2: U = ∆ϕ = ϕ1 − ϕ2 dla punktów A i B odległych od płaszczyzny odpowiednio o x1 i x2.
x1
x2
x2
x1
U = φ1 − φ2 = − ∫ E dx =
qs
∫ 2εε
dx =
0
qs
q
x
x x2 = s ( x2 − x1 ) .
2εε 0 1 2εε 0
(D1.8)
Wobec warunku x2 > x1 jest ϕ1 > ϕ2, czyli potencjał maleje z odległością od równomiernie i
dodatnio (qs > 0) naładowanej nieskończenie wielkiej płaszczyzny. Potencjał jest symetryczny
względem płaszczyzny – po jej obu stronach maleje.
Na rys. D1.2 pokazano przebiegi zmian natężenia pola elektrycznego E i potencjału ϕ w
funkcji odległości od nieskończenie wielkiej płaszczyzny dla x > 0.
E
x
0
x1
x2
1
2
Rys. D1.2. Natężenie pola elektrycznego E i potencjał ϕ w funkcji odległości
od nieskończenie wielkiej płaszczyzny równomiernie naładowanej dodatnim
ładunkiem powierzchniowym
–2–