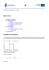Przykład Szybkość zbieności w CTG:

Wykład 5
Nierówność Czebyszewa, CTG
X – zmienna losowa o wartości oczekiwanej
µ i wariancji σ2.
Nierówność Czebyszewa
Dla każdego ε>0
P(| X − µ |> ε ) ≤
σ2
ε2
Przykład
• Samolot zabiera 80 osób. Zakładając, że
waga pasażerów ma pewien rozkład o
wartości oczekiwanej 80 kg i wariancji 10
kg2 oszacować za pomocą nierowności
Czebyszewa prawdopodobieństwo tego,
że łączna waga pasażerów przekroczy
7000 kg.
Wnioski z nierówności Czebyszewa
Centralne Twierdzenie Graniczne
1. Każdy estymator nieobciążony, którego
wariancja maleje do zera wraz ze
wzrostem rozmiaru próby jest zgodny.
• Jeżeli Y ma rozkład normalny to rozkład
(próbkowy) Y jest też normalny (z
mniejszym SD).
• Nawet jeżeli Y nie ma rozkładu
normalnego to dla dużych n rozkład Y jest
bliski normalnemu (warunek dostateczny –
rozkład Y ma skończoną wariancję).
2. Jeżeli wariancja badanego rozkładu jest
skończona to średnia z próby jest
zgodnym estymatorem wartości
oczekiwanej.
Szybkość zbieżności w CTG:
• Co to znaczy ``duże’’ n ?
• To zależy od tego jak bliski rozkładowi
normalnemu jest rozkład Y i jak dużej
dokładności przybliżenia oczekujemy.
• Jeżeli Y ma rozkład normalny to wystarczy
n=
.
• Jeżeli rozkład Y jest w przybliżeniu
symetryczny i nie ma ``ciężkich ogonów’’
to n=30 jest dość duże.
1
Wniosek
• Techniki prezentowane dalej na tym kursie,
dotyczące konstrukcji przedziałów ufności dla µ i
testowania hipotez o średnich, mogą być
również stosowane, gdy rozkład pojedynczych
obserwacji nie jest normalny, o ile tylko rozmiar
prób jest „wystarczająco” duży i rozkład nie ma
„ciężkich ogonów”.
• Założenie o niezależności poszczególnych
obserwacji jest niezbędne.
Przykład:
• Producent ocenia, że 2% jego wyrobów jest
wadliwych. Wyroby te paczkuje się po 40 w jednym
opakowaniu.
• Y = liczba wadliwych wyrobów w losowo wybranej
paczce. Y ma rozkład .........................................
• Niech p̂ = Y/40 = frakcja elementów wadliwych.
• P( p̂ = r ) =
Gdybyśmy otworzyli tysiące paczek, to rozkład frakcji
liczby wadliwych elementów w paczce byłby zgodny
z rozkładem wyliczonym na poprzedniej stronie.
Prawdziwa wartość p jest 0.02 i nie jest nawet
możliwa do zaobserwowania w pojedynczym
eksperymencie, ale na ogół otrzymamy wartości
bliskie 0.02. P-stwo, że p̂ = 0.025 wynosi 36%.
P-stwo, że nasza ocena będzie różnić się nie więcej
niż o 0.03 od prawdziwej wartości wynosi:..............
Rozkład próbkowy estymatora
dla p w rozkładzie dwupunktowym
• Y = liczba sukcesów w n próbach
• y = zaobserwowana liczba sukcesów
• p̂ = Y/n jest estymatorem p
Rozkład p̂ wyznaczamy przy pomocy
(dwumianowego) rozkładu Y!
Pr( pˆ = 0) = Pr(Y = 0) = (1)(.02)0 (.98)40 = 0.45
Pr( pˆ = 0.025) = Pr(Y =1) = (40)(.02)1(.98)39 = 0.36
Pr( pˆ = 0.05) = Pr(Y = 2) = (780)(.02)2 (.98)38 = 0.14
Pr( pˆ = 0.075) = Pr(Y = 3) = (9880)(.02)3 (.98)37 = 0.04
Pr( pˆ ≥ 0.1) = Pr(Y ≥ 4) ≈ 0.01
Przykład
• n=40 i p = 0.02. Jakie jest p-stwo, że
estymator częstości przekracza dwukrotnie (lub
więcej) prawdziwą wartość?
Zatem, jeżeli znajdziemy 3 lub więcej wyrobów
wadliwych w jednej paczce mamy podstawy, żeby
kwestionować twierdzenie producenta o p!
2
Zależność od rozmiaru próby
•
•
•
•
•
•
•
Y ma rozkład Bernoulliego (n,p)
µY=np
Var (Y)=np(1-p)
p̂ =
µ p̂ =
Var ( p̂ )=
UWAGA - p̂ jest nieobciążonym i zgodnym
estymatorem parametru p.
• Dla dużych n rozkład p̂ można przybliżać
rozkładem normalnym.
• Gdy n rośnie, to wariancja
...............
i estymator staje się bardziej ....................
• Przykład; p=0.3.
Rozkład p̂ (gdy p=0.3)
Estymacja wariancji
1
∑ ( X i − µ )2
n
1
S2 =
∑ ( X i − X )2
n −1
2
E ( S0 ) = E ( S 2 ) = σ 2
2
S0 =
n
P(0.25≤ p̂ ≤0.35)
10
0.5
20
0.535
40
0.612
80
0.728
500
0.987
1
(E( X i − µ )4 − σ 4 )
n
E ( X − µ ) 4 (n − 3) 4
Var ( S 2 ) =
−
σ
n
n(n − 1)
2
Var ( S 0 ) =
3
Wnioski
• S02 i S2 są nieobciążonymi estymatorami
wariancji
• Jeżeli czwarty moment rozkładu jest
skończony to są one również
estymatorami zgodnymi
Rozkład χ2
• Definicja: Niech Y1, … Yk będą
niezależnymi zmiennymi losowymi o
rozkładzie N(0,1). Suma kwadratów tych
zmiennych ma rozkład χ2k (rozkład chikwadrat z k stopniami swobody).
Wniosek
• Jeżeli rozmiar próby jest dostatecznie
duży (n>30) to rozkład S2 można
przybliżać rozkładem normalnym o
wartości oczekiwanej σ2 i wariancji
2 σ4 /(n-1).
Estymator wariancji w rozkładzie
normalnym
• Jeżeli obserwacje pochodzą z rozkładu
normalnego to (n-1)S2/σ2 ma rozkład chikwadrat z n-1 stopniami swobody.
Wartość oczekiwana i wariancja
• Jeżeli zmienna X ma rozkład chi-kwadrat z
k stopniami swobody to jej wartość
oczekiwana wynosi
• a jej wariancja wynosi 2k.
• Wniosek z CTG – rozkład chi-kwadrat z k
stopniami swobody przybliżamy przez
N(µ=k, σ2=2k).
Przykład
• W pewnym kraju wzrost mężczyzn można
modelować za pomocą rozkładu
normalnego. W celu oszacowania
wariancji tego rozkładu wylosowano 36
mężczyzn. Oszacuj prawdopodobieństwo,
że wyliczona wariancja próbkowa odchyli
się od rzeczywistej wartości tego
parametru o ponad 4 cm2, jeżeli
rzeczywiste odchylenie standardowe
wynosi σ=5 cm.
4